
梯度 ■梯度性质 ·梯度与方向导数:数量场在一点沿某方向的方向导数 等于梯度在该方向的投影: ·梯度与等值面:数量场中一点处的梯度垂直于该点处 的等值面,且指向数量增大一方。 ou gradu.o al du. gradu= du a lexu@mail.xidian.edu.cn 6
梯度 梯度性质 • 梯度与方向导数:数量场在 点沿某方向的方向导数 一点沿某方向的方向导数 等于梯度在该方向的投影; • 梯度与等值面:数量场中 点处的梯度垂直于该点处 一点处的梯度垂直于该点处 的等值面,且指向数量增大一方。 u 0 ˆ gradu uuu gradu= x y z x y z lexu@mail.xidian.edu.cn 6

梯度 ■ 例求曲面2xz2-3xy-4x=7在其上点M1,-1,2 处的切平面方程 [解] ·该曲面是数量场u=2xz2-3xy-4x的一张等值面; 。由梯度性质可知点处的法向方向与梯度同向 gradu ly=(2=2-3y)i-3xj+4xzk ly=7i-3j+8k 。由此可得切平面方程 7(x-1)+3y+1)+8(z-2)=0 =7x-3y+82=26 lexu@mail.xidian.edu.cn
梯度 例 求曲面2xz2-3xy-4x=7在其 点上 M(1,-1,2) 处的切平面方程 [解] 该曲面是数量场 2 2 • 该曲面是数量场u=2xz2-3xy-4x的 张等值面 一 ; • 由梯度性质可知点M处的法向方向与梯度同向 由此可得切平面方程 2 ˆ ˆ ˆˆ ˆ ˆ grad | (2 3 ) 3 4 | 7 3 8 M M u z y i xj xzk i j k • 由此可得切平面方程 7( 1) 3( 1) 8( 2) 0 xyz lexu@mail.xidian.edu.cn 7 7 3 8 26 xyz
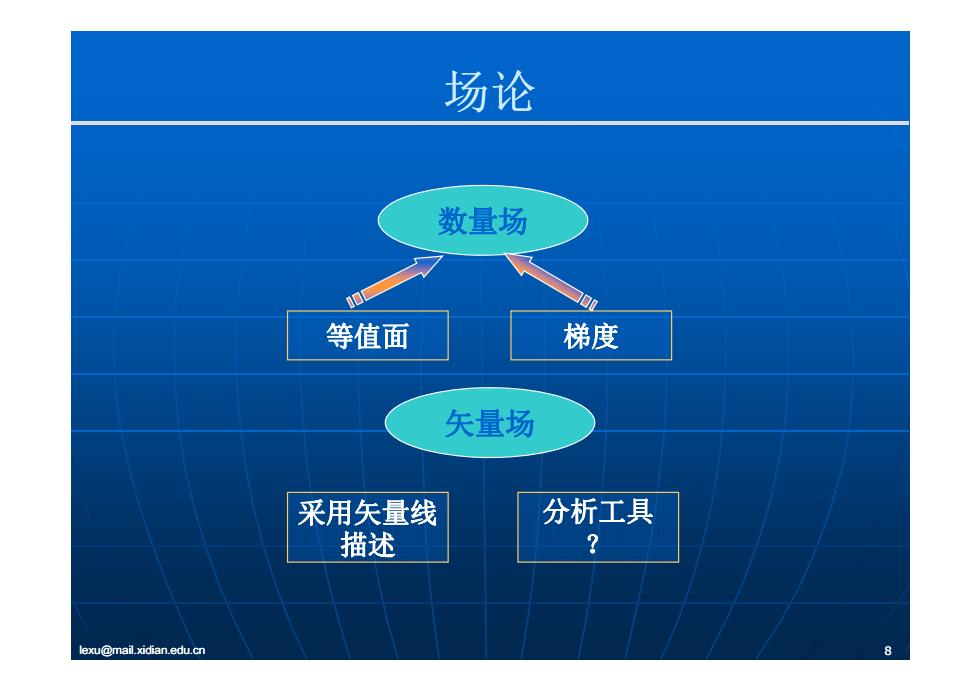
场论 数量场 等值面 梯度 矢量场 采用矢量线 分析工具 描述 ? lexu@mail.xidian.edu.cn
场论 数量场 等值面 梯度 矢量场 采用矢量线 分析工具 描述 ? lexu@mail.xidian.edu.cn 8

第3讲矢量场分析 ■矢量场的通量与散度: 。矢量场的通量 ·矢量场的散度 ■矢量场的环量与旋度: ·矢量场的环量 。矢量场的旋度 lexu@mail.xidian.edu.cn
第3讲 矢量场分析 矢量场的通量与散度: • 矢量场的通量 • 矢量场的散度 矢量场的环量与旋度: • 矢量场的环量 • 矢量场的旋度 lexu@mail.xidian.edu.cn 9
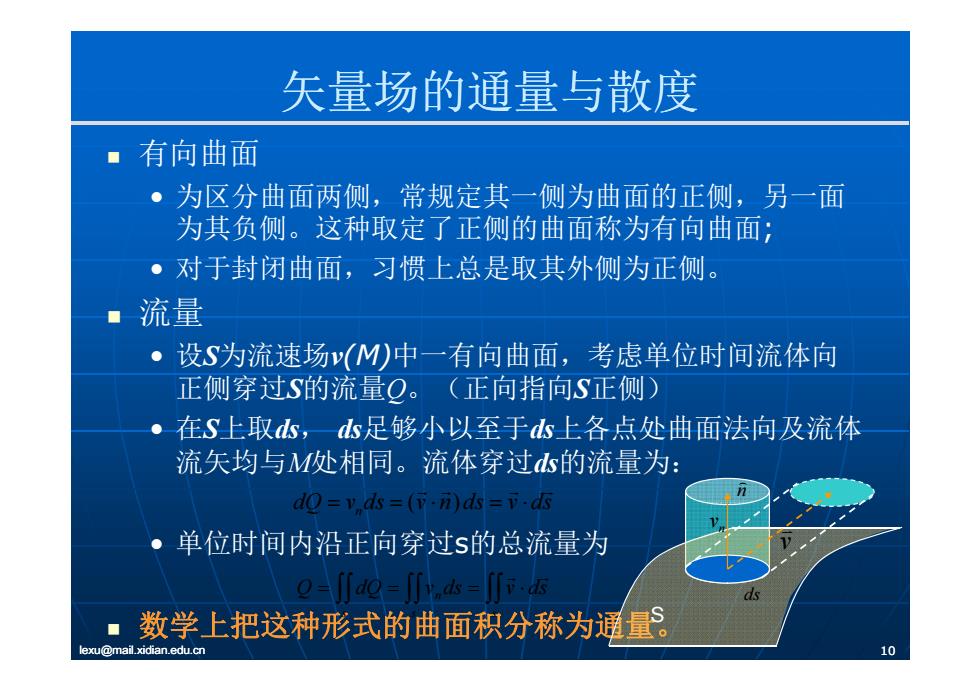
矢量场的通量与散度 ■有向曲面 ·为区分曲面两侧,常规定其一侧为曲面的正侧,另一面 为其负侧。这种取定了正侧的曲面称为有向曲面 ·对于封闭曲面,习惯上总是取其外侧为正侧。 ■流量 ·设S为流速场v(M)中一有向曲面,考虑单位时间流体向 正侧穿过S的流量Q。(正向指向S正侧) ·在S上取s,s足够小以至于上各点处曲面法向及流体 流矢均与M处相同。流体穿过s的流量为: d0=v水=()=下-d 。单位时间内沿正向穿过s的总流量为 g=川g=s=厅s ds 数学上把这种形式的曲面积分称为通量 lexu@mail.xidian.edu.cn 10
矢量场的通量与散度 有向曲面 • 为区分曲面两侧,常规定其 侧为曲面的正侧 常规定其 一侧为曲面的正侧,另 面一 面 为其负侧。这种取定了正侧的曲面称为有向曲面 ; • 对于封闭曲面,习惯上总是取其外侧为正侧 。 流量 • 设 S为流速场 v(M)中 有向曲面 一 ,考虑单位时间流体向 考虑单位时间流体向 正侧穿过 S的流量 Q。(正向指向 S正侧) • 在 S上取 ds, ds足够小以至于 ds上各点处曲面法向及流体 上各点处曲面法向及流体 流矢均与 M处相同。流体穿过ds的流量为: n dQ v ds v n ds v ds ( ) • 单位时间内沿正向穿过 s的总流量为 M n v v ( ) n dQ v ds v n ds v ds Q dQ d d lexu@mail.xidian.edu.cn 10 数学上把这种形式的曲面积分称为通量。S ds s s n s Q dQ v ds v ds