
§8.1假设检验 由长期实践可知,标准差较稳定,设o=0.015, 则X~N(4,0.0152),其中u未知. 问题:根据样本值判断=0.5还是4≠0.5. 1°提出两个对立假设H4=4=0.5和H1:4≠4· 2°结合合理法则,再利用已知样本作出判断是接受 假设H(拒绝假设H1),还是拒绝假设H(接受假设H1), 如果作出的判断是接受o,则4=4, 即认为机器工作是正常的,否则,认为是不正常的. 6/51
由长期实践可知, 标准差较稳定, 设 0.015, ~ ( , 0.015 ), 2 则 X N 其中 未知. 问题: 根据样本值判断 0.5还是 0.5 . 1 提出两个对立假设 : 0.5 : . H0 0 和 H1 0 2 结合合理法则,再利用已知样本作出判断是接受 假设H0 (拒绝假设H1 ), 还是拒绝假设H0 (接受假设H1 ). 如果作出的判断是接受H0 , 即认为机器工作是正常的, 否则, 认为是不正常的. , 则 0 §8.1 假设检验 6/51

§8.1假设检验 检验方法(即合理的法则):对于未知参数,仍然从其点估 计量开始讨论,将未知参数与其点估计量进行比较 由于要检验的假设涉及总体均值,故可借助于样本均值来 判断 因为X是的无偏估计量 若过分大,则有理由 所以若H,为真则x-4不应太大 怀疑H,的正确性 当H,为真时X-凸NO, 这里的检验统计量和分 布均不含任何未知参数 衡量下一4的大小可归结为衡量二么的大小 o//n 于是可以选定一个适当的正数k, 7151
由于要检验的假设涉及总体均值, 故可借助于样本均值来 判断. 因为X 是 的无偏估计量, , | | , 所以若H0 为 真 则 x 0 不应太大 ~ (0,1), / , 0 0 N n X H 当 为真时 , / | | | | 0 衡 量 0 的大小可归结为衡量 的大小 n x x 于是可以选定一个适当的正数k, §8.1 假设检验 这里的检验统计量和分 布均不含任何未知参数 检验方法(即合理的法则):对于未知参数,仍然从其点估 计量开始讨论,将未知参数与其点估计量进行比较 若过分大,则有理由 怀疑H0的正确性 7/51
§8.1假设检验 此即假定H,正确 时的小概率事件 当观察值c满足工一么≥k时,拒绝假别, o//n 反之,当观察值x满足 下一<k时,接受假. o/n 如何选取k呢,先看以下事实: 由于作出决策的依据是一个样本,当实际 上H为真时,仍可能作出拒绝H的决策,这种 可能性是无法消除的,这是一种错误。 8/51
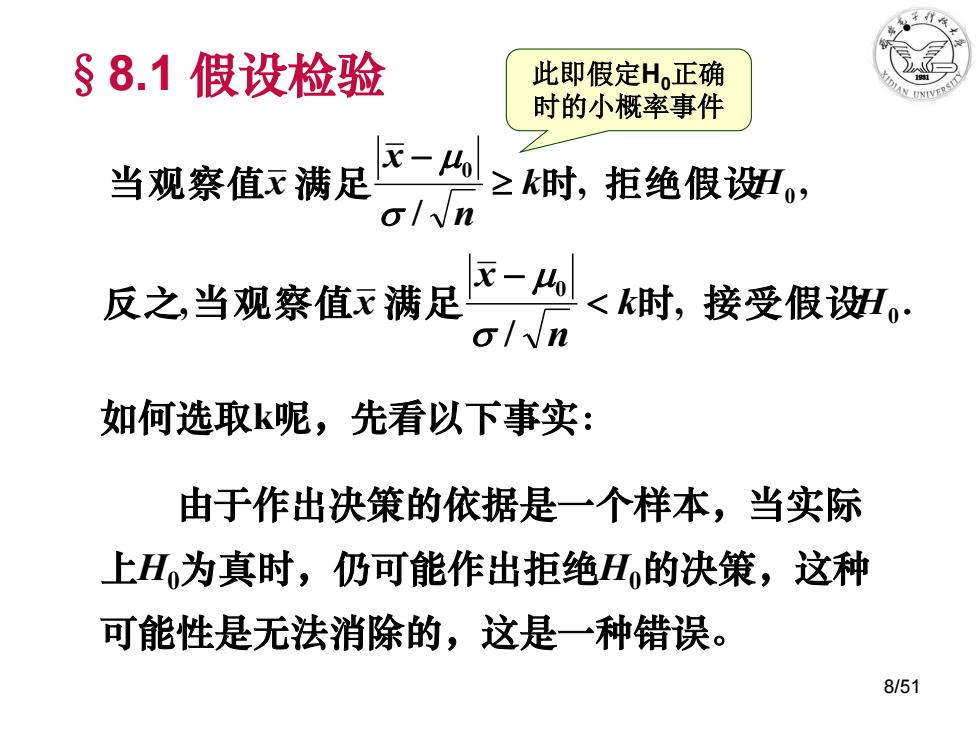
, , / 0 0 k H n x 当观察值x 满 足 时 拒绝假设 , . / , 0 0 k H n x 反 之 当观察值x 满 足 时 接受假设 §8.1 假设检验 如何选取k呢,先看以下事实: 由于作出决策的依据是一个样本,当实际 上H0为真时,仍可能作出拒绝H0的决策,这种 可能性是无法消除的,这是一种错误。 此即假定H0正确 时的小概率事件 8/51

§8.1假设检验 ·因此自然希望将犯这类错误的概率控制在一定限 度之内,即给出一个较小的数a(0<<1),使犯这类 错误的概率不超过a,即使得: P{拒绝HoH为真}≤ 因为当为真时前述的统计= X-4~N0,1), o/n 及其分布,不含任何知参数, 由最大允许错误概,令上式取等号得 P拒绝H,1H,为真=P一4≥k3=a, o/n 9/51
§8.1 假设检验 因此自然希望将犯这类错误的概率控制在一定限 度之内,即给出一个较小的数α(0<α<1),使犯这类 错误的概率不超过α,即使得: P{拒绝H0 |H0为真}α 及其分布,不含任何未知参数, 因为当 为真时前述的统计量 ~ (0,1), / 0 0 N n X H Z 由最大允许错误概率,令上式取等号得 } , / { | } { 0 0 0 k n x P 拒 绝H H 为 真 P 9/51

§8.1假设检验 由标准正态分布分位点的定义得k=z/2, 当 ≥乙a/2时,拒绝H) 下-4 <za2时,接受H o/n o/n 前述的错?{拒绝H|当H为真},称为“弃真” 类错误,也可记作: P,{拒绝H}:表示参数取4时事件拒绝H的概率 或者 PeH,拒绝Ho}:表示参数陬H规定值时事代拒绝H} 的概率 10/51
由标准正态分布分位点的定义得 , . / , , / / 2 0 0 / 2 0 0 z H n x z H n x 当 时 拒 绝 时 接 受 , / 2 k z §8.1 假设检验 的概率 拒 绝 表示参数 取 规定值时事件拒 绝 或 者 拒 绝 表示参数 取 时事件 拒 绝 的概率 类错误,也可记作: 前述的错误 拒 绝 当 为 真 ,称为“弃真” { }: { } { }: { } { | } 0 0 0 0 0 0 0 0 0 0 P H H H P H H P H H H 10/51