
即 △y=f'(u)△u+0△w △x≠0时, 少y=f'( △x ’△x △x 由于u=p(x)在x点可导,故u在x点连 续,所以当△x→0时, △u=p(x+△x)-p(x)-→>0 故lim Av=M(u)lim Aulim alim u-f(u)() △x→0△x Ar→0△X△u→0Ar→0△X 即 [f(p(x)]'=f'(u)p'(x)。 此定理可以推广以任意有限个函数复合情形。例 如:v=yw(x)在x点可导,M=p(v)在x点的对应点 v(v=w(x)可导,y=f4又在v点的对应点u(u=p(v)可导
8 即 = + y f u u u ( ) x 0时, ( ) y u u f u x x x = + 由于u x = ( )在x点可导,故u在x点连 续,所以当 →x 0时, = + − → u x x x ( ) ( ) 0 故 0 0 0 0 lim ( ) lim lim lim x x u x y u u f u x x x → → → → = + = f u x ( ) ( ) 即 [ ( ( ))] ( ) ( ) f x f u x = 。 此定理可以推广以任意有限个函数复合情形。例 如 : v x = ( ) 在 x 点可导, u v = ( ) 在 x 点的对应点 v(v x = ( ))可导,y f u = ( )又在v点的对应点u( ( ) u v = )可导

则复合函数f{p[y(x)}在x点可导,且导数为 (f{p[yw(x)]})'=f'()p'(v)w'(x) 或 dy dy du dv dx du dy dx 例1.已知y=cos2x,求。y 解 令y=cosu,u=2x,则有 (cosu)(2.--sinu-2=-2sim2x du dx 例2己知y=(x3-sinx)4,求y'。 解令y=w,u=x3-sinx,则有 yu=(uy(x'-sinxy=4u(3x-cosx) du dx =4(x3-sinx)3(3x2-cosx) 9
9 则 复 合 函 数 f x { [ ( )]} 在 x 点 可 导 , 且 导 数 为 ( { [ ( )]}) ( ) ( ) ( ) f x f u v x = 或 dy dy du dv dx du dv dx = 例1.已知 y x = cos 2 ,求。 y 解 令y u u x = = cos , 2 ,则有 (cos ) (2 ) sin 2 2sin 2 dy du y u x u x du dx = = = − = − 例2 已知 3 4 y x x = − ( sin ) ,求 y 。 解 令 4 3 y u u x x = = − , sin ,则有 4 3 3 2 ( ) ( sin ) 4 (3 cos ) dy du y u x x u x x du dx = = − = − 3 3 2 = − − 4( sin ) (3 cos ) x x x x
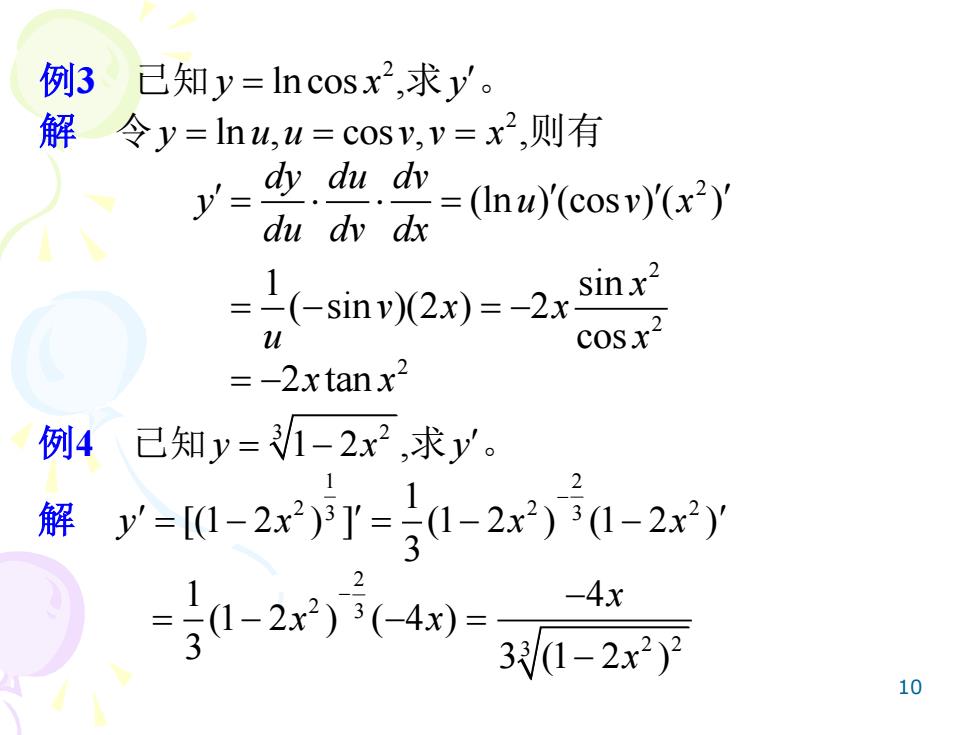
例3已知y=Incosx2,求y'。 解令y=lnw,w=cosy,v=x2,则有 u=(m(cosv( du dy dx -(-snvX2x)=-2rsin Cosx2 =-2xtanx2 例4已知y=1-2x2,求y。 解y=[1-2x2)5Y=0-2x)50-2xy 0-2x)(-4) -4x 3/1-2x2)2 10
10 例3 已知 2 y x = ln cos ,求 y 。 解 令 2 y u u v v x = = = ln , cos , ,则有 2 2 2 (ln ) (cos ) ( ) 1 sin ( sin )(2 ) 2 cos dy du dv y u v x du dv dx x v x x u x = = = − = − 2 = −2 tan x x 例4 已知 3 2 y x = −1 2 ,求 y 。 解 1 2 2 2 2 3 3 1 [(1 2 ) ] (1 2 ) (1 2 ) 3 y x x x − = − = − − 2 2 3 3 2 2 1 4 (1 2 ) ( 4 ) 3 3 (1 2 ) x x x x − − = − − = −