
山东农大 高等数 第十二章习题课 ●基本内容 。典型例题
山东农业大学 高等数学 主讲人:苏本堂 第十二章 习题课 基本内容 典型例题
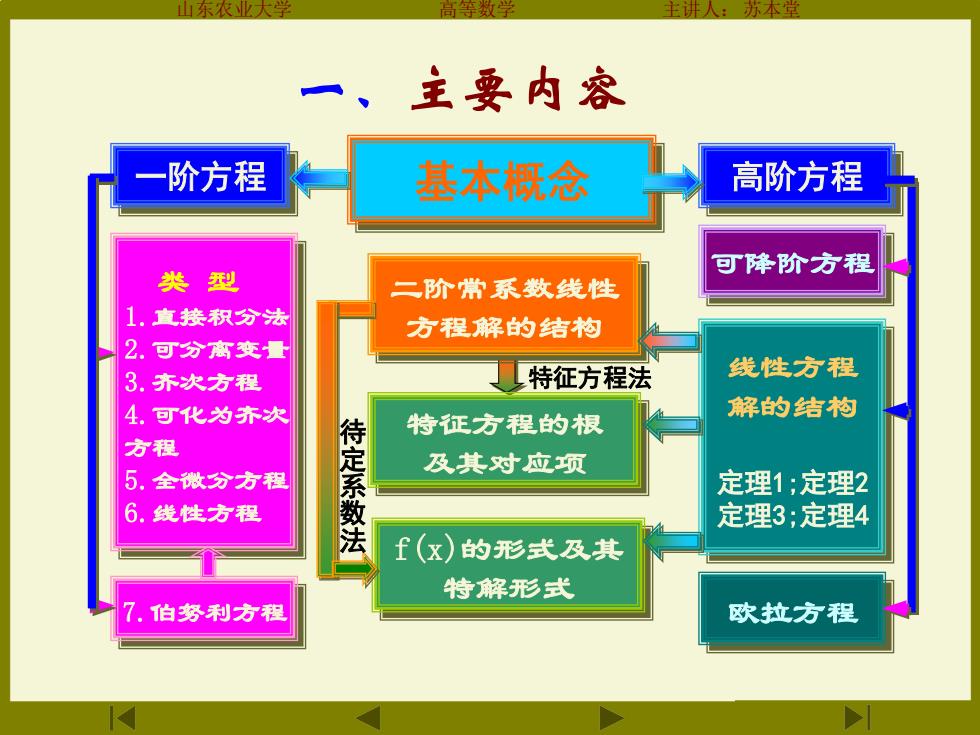
方本 一、主要内容 阶方程 基本概念 高阶方程 类型 可降阶方程 二阶常系数线性 1.直接积分法 方程解的结构 2.可分高变量 3.齐次方程 特征方程法 线性方程 4.可化为齐次 解的结抱 特征方程的根 方程 及其对应项 5.全微分方程 待定系数 定理1;定理2 6.线性方程 定理3;定理4 f(x)的形式及其 特解形式 7.伯努利方程 欧拉方程
山东农业大学 高等数学 主讲人:苏本堂 一阶方程 基本概念 类 型 1.直接积分法 2.可分离变量 3.齐次方程 4.可化为齐次 方程 5.全微分方程 6.线性方程 7.伯努利方程 可降阶方程 线性方程 解的结构 定理1;定理2 定理3;定理4 欧拉方程 二阶常系数线性 方程解的结构 特征方程的根 及其对应项 f(x)的形式及其 特解形式 高阶方程 待 定 系 数 法 特征方程法 一、主要内容

山东农 阶微分方程 三种基本类型 变量可分离 一阶线性 其余类型的方程可借助于变量代换或积 分因子化成基本类型 三种基本类型代表三种典型解法 分离变量法 常数变易法 变量代换是解微分方程的重要思想和重要方法
山东农业大学 高等数学 主讲人:苏本堂 三种基本类型 变量可分离 一阶线性 其余类型的方程可借助于变量代换或积 分因子化成基本类型 三种基本类型代表三种典型解法 分离变量法 常数变易法 变量代换是解微分方程的重要思想和重要方法 一阶微分方程

主计 方本堂 例1.求下列方程的通解 De=o. :(2)xy=Vx2-y2+y; 6x3+3xy2 (3)y'= 2x-y2 ④y= 3x2y+2y3 提示:)因e广+x=ee,故为分离变量方程 -y2e-xdy=e*dx 通解 jo/-0+C
山东农业大学 高等数学 主讲人:苏本堂 例1. 求下列方程的通解 0; 1 (1) 3 2 + = y +x e y y 提示: (1) , 3 3 y x y x e = e e 因 + 故为分离变量方程: 通解 (2) ; 2 2 xy = x − y + y ; 2 1 (3) 2 x y y − = . 3 2 6 3 (4) 2 3 3 2 x y y x xy y + + = − y e y e x y x d d 3 2 − = − e e C y x = + − 3 3 1

(2)xy'=Vx2-y2+y 方程两边同除以x即为齐次方程,令y=x,化为分 离变量方程 >0时,=1-()P+一w= x<0时,=1-()2+一w=-1- 1 (3)y'= 2x-y2 调换自变量与因变量的地位,化为 dr-2x=-y2, 用线性方程通解公式求解
山东农业大学 高等数学 主讲人:苏本堂 方程两边同除以 x 即为齐次方程 , xy = x − y + y 2 2 (2) x 0时, 2 xu = 1− u 2 xu = − 1− u ( ) x y x y y = − + 2 1 ( ) x y x y y = − − + 2 1 令 y = u x ,化为分 离变量方程. 调换自变量与因变量的地位, 2 2 1 (3) x y y − = 2 , d d 2 x y y x − = − 用线性方程通解公式求解 . 化为