
三、上好第一节课 (3)生男生女问题:假定生男生女的机会均等,且生育政策为“若生一 男孩,可继续生育,直到有一女孩出生为止”,长时间后,男孩的数量是否 会增加? (4)生日问题:若一个人出生在一年365天中的每一天的机会相同,那么 对一个有个人的班级,至少有两个人可以在同一天过生日的概率有多大?对 于=10,20,30,.,100,分别计算其概率,其结果与你的想象是否相符? (5)奶茶辨认问题:一女士称她能通过品尝奶茶辨别出是奶先加入还是茶 先加入,现准备8杯奶茶,并告知她其中4杯奶先加入,另4杯茶先加入,让她 品尝辨别,结果她各辨别正确3杯,据此结果,你对该女士的奶茶辨别能力有 何评价?如果准备16杯奶茶,其中8杯奶先加入,另8杯茶先加入,若她各辨别 正确7杯,你又能作何评价? 2010-8-5 11
2010-8-5 11 三、上好第一节课 (3)生男生女问题:假定生男生女的机会均等,且生育政策为“若生一 男孩,可继续生育,直到有一女孩出生为止”,长时间后,男孩的数量是否 会增加? (4)生日问题:若一个人出生在一年365天中的每一天的机会相同,那么 对一个有n个人的班级,至少有两个人可以在同一天过生日的概率有多大?对 于n=10,20,30, .,100,分别计算其概率,其结果与你的想象是否相符? (5)奶茶辨认问题:一女士称她能通过品尝奶茶辨别出是奶先加入还是茶 先加入,现准备8杯奶茶,并告知她其中4杯奶先加入,另4杯茶先加入,让她 品尝辨别,结果她各辨别正确3杯,据此结果,你对该女士的奶茶辨别能力有 何评价? 如果准备16杯奶茶,其中8杯奶先加入,另8杯茶先加入,若她各辨别 正确7杯,你又能作何评价?
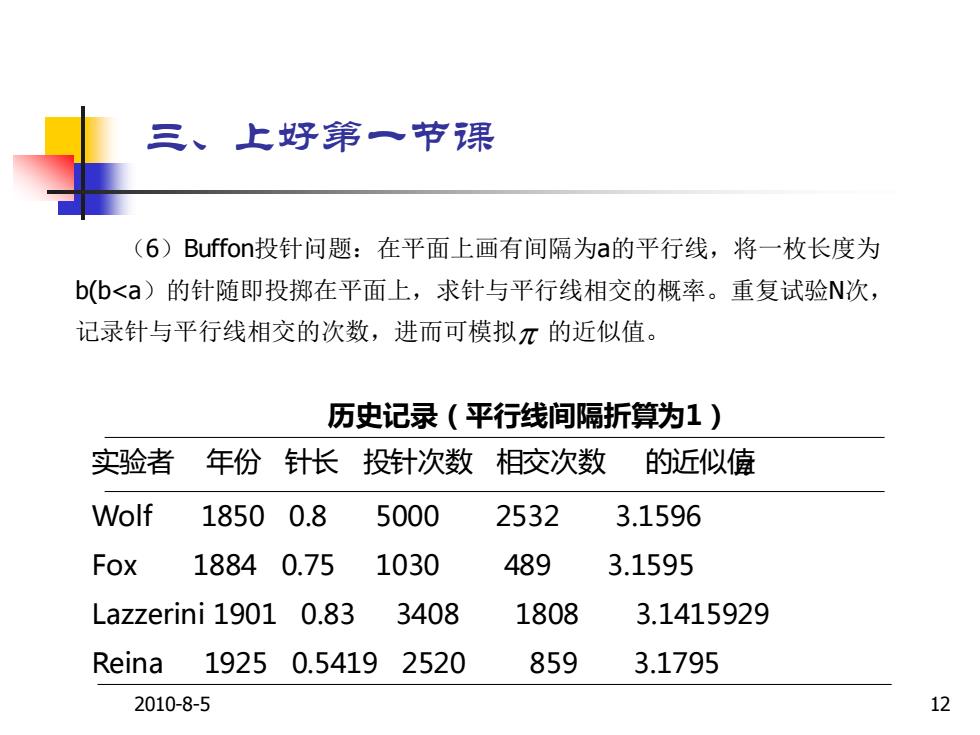
三、上好第一节课 (6)Buffon投针问题:在平面上画有间隔为a的平行线,将一枚长度为 b(b<a)的针随即投掷在平面上,求针与平行线相交的概率。重复试验N次, 记录针与平行线相交的次数,进而可模拟π的近似值。 历史记录(平行线间隔折算为1) 实验者 年份针长投针次数, 相交次数 的近似值 Wolf 18500.8 5000 2532 3.1596 Fox 18840.75 1030 489 3.1595 Lazzerini 1901 0.83 3408 1808 3.1415929 Reina 19250.5419 2520 859 3.1795 2010-8-5 12
2010-8-5 12 (6)Buffon投针问题:在平面上画有间隔为a的平行线,将一枚长度为 b(b<a)的针随即投掷在平面上,求针与平行线相交的概率。重复试验N次, 记录针与平行线相交的次数,进而可模拟 的近似值。 历史记录(平行线间隔折算为1) 实验者 年份 针长 投针次数 相交次数 的近似值 Wolf 1850 0.8 5000 2532 3.1596 Fox 1884 0.75 1030 489 3.1595 Lazzerini 1901 0.83 3408 1808 3.1415929 Reina 1925 0.5419 2520 859 3.1795 三、上好第一节课

三、上好第一节课 (7)敏感性问题调查:在敏感性问题(如大学生考试作弊、婚外恋、 吸毒)调查中,即使采用无记名方式,一般也不能完全消除被调查者的种 种顾虑,从而得不到较为真实的数据和分析结果。通过本课程的学习,你 能否设计出一些更为合理有效的调查方式,以尽可能的消除被调查者的顾 虑,并按你所设计的调查方式,分析在被调查人群中有关问题发生的概率。 (8)匹配问题:每人带一件外形包装相同的礼物参加聚会,将所有礼 物充分混合,再让每人随机拿一件,求至少有一个人拿到自己礼物的概率。 平均来说,有几个人正好拿到自己的礼物? 2010-8-5 13
2010-8-5 13 三、上好第一节课 (7) 敏感性问题调查:在敏感性问题(如大学生考试作弊、婚外恋、 吸毒)调查中,即使采用无记名方式,一般也不能完全消除被调查者的种 种顾虑,从而得不到较为真实的数据和分析结果。通过本课程的学习,你 能否设计出一些更为合理有效的调查方式,以尽可能的消除被调查者的顾 虑,并按你所设计的调查方式,分析在被调查人群中有关问题发生的概率。 (8) 匹配问题:每人带一件外形包装相同的礼物参加聚会,将所有礼 物充分混合,再让每人随机拿一件,求至少有一个人拿到自己礼物的概率。 平均来说,有几个人正好拿到自己的礼物?

四、从样本空间、随机事件到事件域 ={随机试验E的所有可能结果}={o: ■随机事件:Ac2; 随机事件的关系、运算及运算规律; ■事件域:F={与E有关的随机事件的全体} 问题:F是否可由的全体子集构成?若不能, F应至少满足什么条件,才能包含足够感 兴趣的事件? 2010-8-5 14
2010-8-5 14 四、从样本空间、随机事件到事件域 ◼ {随机试验E的所有可能结果}={ }; ◼ 随机事件: ; ◼ 随机事件的关系、运算及运算规律; ◼ 事件域:F={与E有关的随机事件的全体} 问题:F是否可由 的全体子集构成?若不能, F应至少满足什么条件,才能包含足够感 兴趣的事件? = A

四、从样本空间、随机事件到事件域 由所定义的事件的关系及运算,我们自然要求 F中应包含两个特殊事件,即必然事件和不可能事 件,也应至少包括事件的和事件、积事件、差事件、 对立事件等,可证只要F满足: (i)2∈F; (i)A∈F→A∈F; (i)A,A2,.,An∈F→A1UA2UUAn∈F. 则F至少可包含上述各种事件。 2010-8-5 15
2010-8-5 15 四、从样本空间、随机事件到事件域 由所定义的事件的关系及运算,我们自然要求 F中应包含两个特殊事件,即必然事件和不可能事 件,也应至少包括事件的和事件、积事件、差事件、 对立事件等,可证只要F满足: (i) (ii) (iii) 则F至少可包含上述各种事件。 , , , . ; ; A1 A2 A F A1 A2 A F A F A F F n n