
定理3(收敛定理,展开定理) 设f(x)是周期为2π的 周期函数,并满足狄利克雷(Dirichlet)条件 1)在一个周期内连续或只有有限个第一类间断点: 2)在一个周期内只有有限个极值点 则f(x)的傅里叶级数收敛,且有 注意:函数展成 傅里叶级数的条 件比展成幂级数 n= 的条件低得多 f(x). x为连续点 x为间断点 2 其中an,bn为f(x)的傅里叶系数,(证明略) HIGH EDUCATION PRESS 上页下页返回结束
定理3 (收敛定理, 展开定理) 设 f (x) 是周期为2的 周期函数, 并满足狄利克雷( Dirichlet )条件: 1) 在一个周期内连续或只有有限个第一类间断点; 2) 在一个周期内只有有限个极值点, 则 f (x) 的傅里叶级数收敛 , 且有 = f (x) , , 2 ( ) ( ) + − f x + f x x 为间断点 其中 an bn , 为 f (x) 的傅里叶系数 . ( 证明略 ) x 为连续点 注意: 函数展成 傅里叶级数的条 件比展成幂级数 的条件低得多. 简介 目录 上页 下页 返回 结束

例1.设fx)是周期为2π的周期函数,它在[-π,π) 上的表达式为 ro-fhi π≤x<0 sx< 将f(x)展成傅里叶级数 解:先求傅里叶系数 comdx -2-+号01-ewxd =0 (n=0,1,2,.) HIGH EDUCATION PRESS 机动目录上页下页返回结束
例1. 设 f (x) 是周期为 2 的周期函数 , 它在 上的表达式为 − − = x x f x 1, 0 1, 0 ( ) 解: 先求傅里叶系数 = − + − 0 0 1 cos d 1 ( 1)cos d 1 nx x nx x = 0 ( n = 0 ,1, 2 , ) 将 f (x) 展成傅里叶级数. o y x −1 − 1 机动 目录 上页 下页 返回 结束

7 (-)sin mdx+ ]+g-w时 -r1- 当n=1,3,5,. 当n=2,4,6,. (-0<x<+0,x≠0,±π,±2π,.) HIGH EDUCATION PRESS 机动目录上页下页返回结束
= − + − 0 0 1 sin d 1 ( 1)sin d 1 nx x nx x 0 1 cos − = n nx 0 1 cos − + n nx n n 1 cos 2 = − n n 1 ( 1) 2 = − − = , 4 n 0 , 当n =1, 3 , 5 , 当n = 2 , 4 , 6 , f x = sin x + 4 ( ) sin 3x + 3 1 − + − + k x k sin(2 1) 2 1 1 (− x + , x 0 , , 2 , ) 机动 目录 上页 下页 返回 结束
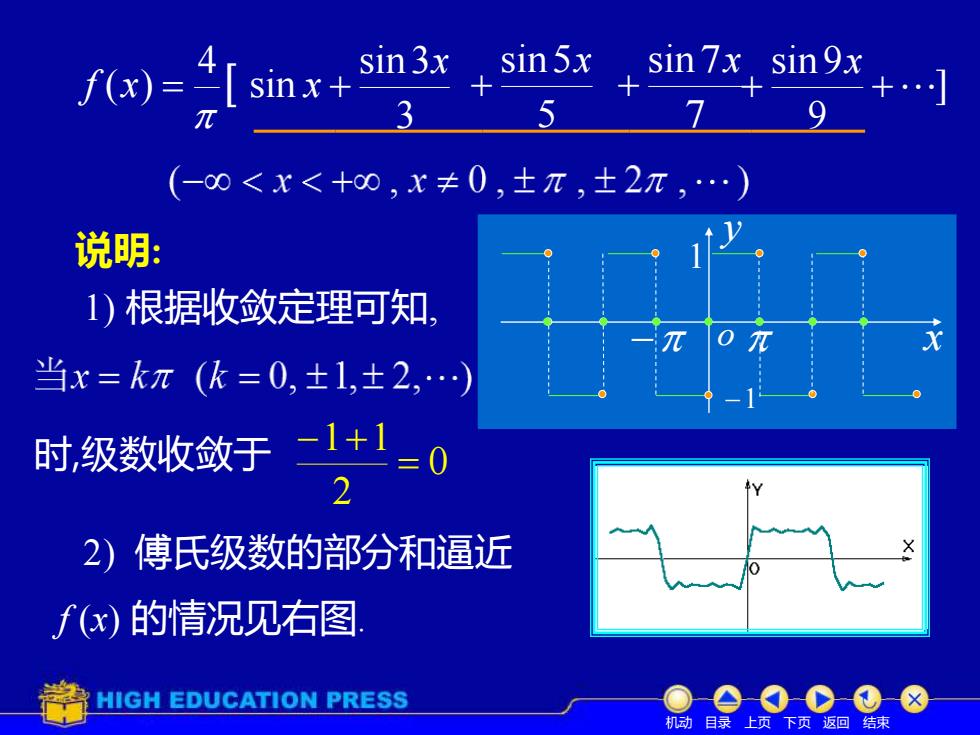
sinx+ in3x, sin5x,sin7x sin9x 3 5 (-0<x<十0,x≠0,土π,士2π,.) 说明: 1)根据收敛定理可知」 当x=kπ(k=0,±1,±2,.) 时级数收敛于 -1+1=0 2 2)傅氏级数的部分和逼近 f(x)的情况见右图 HIGH EDUCATION PRESS e0C8 机动目录上页下页返回结束
7 sin 7x + ] 9 sin 9 + + x 1) 根据收敛定理可知, 时,级数收敛于 0 2 1 1 = − + 2) 傅氏级数的部分和逼近 3 sin 3 sin 4 ( ) x f x = x + 5 sin 5x + o y x −1 − 1 说明: f (x) 的情况见右图. 机动 目录 上页 下页 返回 结束

例2.设f(x)是周期为2元的周期函数,它在[-π,π) 上的表达式为 fW- -π≤x<0 3π-2π,兀 0, 0≤x<π 将f(x)展成傅里叶级数. 解-5心x-2xdx=[芝]2-月 a.-gf儿-o c cosnx l-cosnπ n nπ HIGH EDUCATION PRESS 机动目录上页下页返回结束
x − o y 例2. 上的表达式为 将 f (x) 展成傅里叶级数. 解: − = a f (x)d x 1 0 − = 0 cos d 1 x nx x − = a f x nx x n ( )cos d 1 − = 0 d 1 x x − = 0 2 2 1 x 2 = − − = + 0 2 1 sin cos n nx n x nx 2 1 cos n − n = −3 −2 2 3 设 f (x) 是周期为 2 的周期函数 , 它在 机动 目录 上页 下页 返回 结束