
第九章多元函戴微分法及并应用班级: 姓名: 序号: 1多元函数的基本概念 一、填空、选择题 L函数:=x-√少的定义域为 之西数=0的定义线为 3.函数1=4-x2-y2-2+ +户:的定义城为 1 4. sin xy= y 5.设函数f(x,y) y y=0 (A)不存在 (B)等于1 (C)等于0 (D)等于2 6.设函数fx,)=+y 10 +0,则f0x0 x2+y2=0 (A)处处连续: (⑧)处处有极限,但不连续: (C)仅在(0,0)点连续: (D)除(0,0)点外处处连续 二、计算下列极限 1- ytan xy 2.(02
第九章 多元函数微分法及其应用 班级: 姓名: 序号: 1 1 多元函数的基本概念 一、填空、选择题 1. 函数 z = x − y 的定义域为 . 2 函数 2 2 arccos x y z u + = 的定义域为 . 3. 函数 1 1 4 2 2 2 2 2 2 + + − = − − − + x y z u x y z 的定义域为 . 4. y xy x y sin lim ( , )→(3,0) = . 5.设函数 = + = 0 0 0 1 sin 1 sin ( , ) x y x y x y y x f x y ,则极限 lim ( , ) ( , ) (0,0) f x y x y → ( ) (A)不存在 (B)等于 1 (C)等于 0 (D)等于 2 6.设函数 + = + = + 0 0 0 ( , ) 2 2 2 2 2 2 x y x y x y x y f x y ,则 f x y ( , ) ( ) (A) 处处连续; (B) 处处有极限,但不连续; (C) 仅在(0,0)点连续; (D) 除(0,0)点外处处连续 二、计算下列极限 1. xy xy x y 2 4 lim ( , ) (0,0 − + → ) 2. x y xy x y tan lim ( , )→(0,2)

第九章多元函数撒分法及其应用班级: 姓名: 序号: 2-3习题 一、填空、选择题 1、设:=nx+y2),则全微分d止= 2、设fx,y)=xy2+2+x2,则f(1,02)= 3曲线, 4一在点(2,4,5)处的切线对于x轴的倾角为 y=4 4设:m片则会+房 5、=fx,y)在P(oo)处(x,y)、,(x,y)存在是函数在该点可微分的.() (A)必要条件: (B)充分条件: (C)充要条件: (D)既非必要亦非充分条件 二、求下列函数的偏导数 1、z=simx)+cos2(x 2、=(1+x 3u= 三设:的,求证会y2
第九章 多元函数微分法及其应用 班级: 姓名: 序号: 2 2-3 习题 一、填空、选择题 1、设 ln( ) 2 z = x + y ,则全微分 dz = . 2、设 2 2 2 f (x, y,z) = xy + yz + zx ,则 f xz (1,0,2) = . 3、曲线 = + = 4 4 2 2 y x y z 在点 (2,4,5) 处的切线对于 x 轴的倾角为 . 4、设 x y z = x sin ,则 = + y z y x z x . 5、 z = f (x, y) 在 ( , ) 0 0 0 P x y 处 f (x, y) x 、 f (x, y) y 存在是函数在该点可微分的 ( ) (A)必要条件; (B)充分条件; (C)充要条件; (D)既非必要亦非充分条件. 二、求下列函数的偏导数 1、 sin( ) cos ( ) 2 z = xy + xy 2、 y z = (1+ xy) 3、 z y u = x 三、设 ) 1 1 ( x y z e − + = ,求证 z y z y x z x 2 2 2 = +

第九章多元函戴横分法及其应用班级: 姓名: 序号: 日,设汤教:,来器等器 五、求下列函数的全微分 1、=xy4 y 2、2=- 3、u=x
第九章 多元函数微分法及其应用 班级: 姓名: 序号: 3 四、设函数 x y z = arctan ,求 , 2 2 2 2 2 x y z y z x z , . 五、求下列函数的全微分 1、 y x z = xy+ 2、 2 2 x y y z + = 3、 yz u = x

第九章多元函数撒分法及其应用班级: 姓名: 序号: 4一5习题 1设:=e,面x=如=,则先 么、设z=acan(,而y=e,则 模:rh,面=3-2,*袋等 4、求下列函数的一阶偏导数(其中∫具有一阶连续偏导数) (1)z=f(x2-y2,e9) (2)u=f(x,xy,xyz) 黄:心+,其中/其精=0数票需 6设:=,其中了具有=阶连续偏导数,求器司 800 g
第九章 多元函数微分法及其应用 班级: 姓名: 序号: 4 4—5 习题 1、设 x y z e −2 = ,而 3 x = sin t, y = t ,则 = dt dz . 2、设 z = arctan( xy) ,而 x y = e ,则 = dx dz . 3、设 z u ln v 2 = ,而 v x y y x u = , = 3 − 2 ,求 , y z x z . 4、求下列函数的一阶偏导数(其中 f 具有一阶连续偏导数) (1) ( , ) 2 2 xy z = f x − y e (2) u = f (x, xy, xyz) 5、设 z = f (x 2 + y 2) ,其中 f 具有二阶导数,求 , 2 2 2 x y z x z . 6、设 ( , ) y x z = f x ,其中 f 具有二阶连续偏导数,求 2 2 2 2 2 , , y z x y z x z
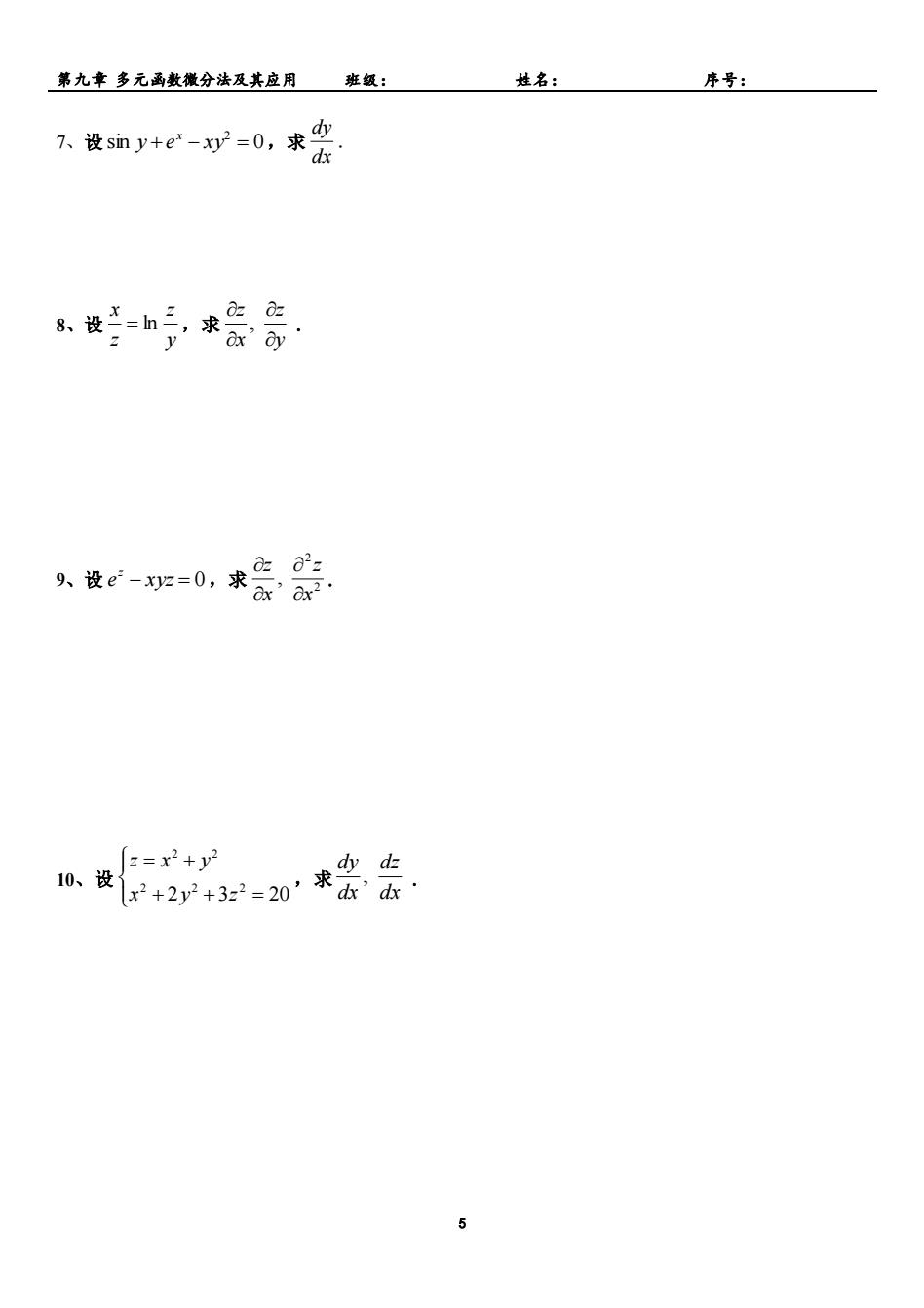
第九章多元函数撒分法及并应用班级: 姓名: 序号: 人设my4e-y=0,求会 8、设-h月*品, 0z 8z r-=0,*器能 2=x2+y2 10、设 +2+3=20求要 dx'dx
第九章 多元函数微分法及其应用 班级: 姓名: 序号: 5 7、设 sin 0 2 y + e − xy = x ,求 dx dy . 8、设 y z z x = ln ,求 , y z x z . 9、设 e − xyz = 0 z ,求 2 2 , x z x z . 10、设 + + = = + 2 3 20 2 2 2 2 2 x y z z x y ,求 , dx dz dx dy