计算机类本科规划教材：《离散数学》课程配套电子教案（PPT课件讲稿）第8章 格与布尔代数

第8章格与布尔代数 定理8.1.7 设<X,≤>和<X,≤2>是格，<X,V1,∧1>和 <X,V2,∧2>是它们导出的代数系统。是格<X,V1,∧>到格 <X,V2,∧2>的格同态，则a,beX,如果a≤1b,必有 a)≤b) 证明：设a≤，b,根据定理8.1.4，a个，b=a,由于f是格 <X,V1,∧>到格<X2,V2,∧>的格同态，所以aa∧1b)= f(a)Λf(b),再由定理8.1.4，f(a)≤2f(b)。 定理8.1.7说明格同态是保序的。一般地说，定理8.1.7 的逆并不成立。 【例8.3】设Aa,b,c,d,e},<A,>是格，其哈斯图如图 8.3所示，RA)是A的幂集合，R<x,>∈RA)∧yeP(A)∧ xSy是RA)上的偏序关系。<R),R>也是格。作映射 f:A→P(A),定义为：x∈A,x)=yyeA且y≤x,即： Aa)a,b,c,d,er=A,Ab)b,er,Ac)cer,Ad)=der, fRe)=e。证明f是保序的，但不是格同态

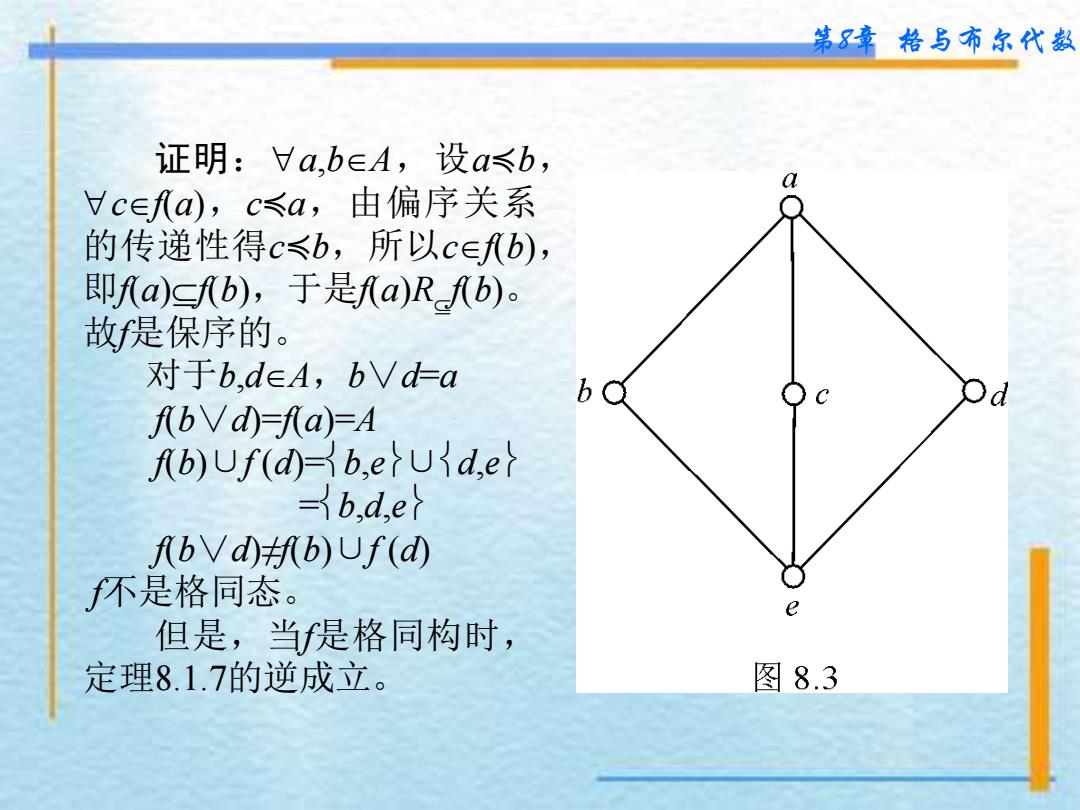
第8章 格与布尔代数 定理8.1.7 设X1 ,≼1 和X2 ,≼2 是格，X1 ,∨1 ,∧1 和 X2 ,∨2 ,∧2 是它们导出的代数系统。f是格X1 ,∨1 ,∧1 到格  X2 ,∨2 ,∧2  的格同态 ， 则 a,bX1 ， 如 果 a≼1 b ， 必 有 f(a)≼2 f(b) 证明：设a≼1 b，根据定理8.1.4，a∧1 b=a，由于 f 是格 X1 ,∨1 ,∧1 到格X2 ,∨2 ,∧2 的格同态，所以f(a)=f(a∧1 b)= f (a)∧2 f (b)，再由定理8.1.4，f (a)≼2 f (b)。 定理8.1.7说明格同态是保序的。一般地说，定理8.1.7 的逆并不成立。 【例8.3】设A=a,b,c,d,e，A,≼是格，其哈斯图如图 8.3所示，P(A)是A的幂集合，R =x,y|xP(A)∧yP (A)∧ xy是P(A)上的偏序关系。P(A), R 也是格。作映射 f：A→P (A)，定义为：xA，f(x)= y|yA且y≼x，即： f(a)=a,b,c,d,e=A ， f(b)=b,e ， f(c)=c,e ， f(d)=d,e ， f(e)=e。证明f是保序的，但不是格同态

第8章格与布尔代数 证明：Ha,beA,设a≤b, Vca),c≤a,由偏序关系 的传递性得c≤b,所以c∈b), 即a)sb),于是a)Rb)。 故是保序的。 对于b,deA,bVd=a b Abd)fa)=A Ab)Uf(d)=b.erUd.ef =b,der fbd)tb)uf(d) 不是格同态。 e 但是，当f是格同构时， 定理8.1.7的逆成立。 图8.3

第 8 章 格与布尔代数 证明 ：  a , b  A ， 设 a ≼ b ，  c f( a ) ， c ≼ a ，由偏序关系 的传递性得 c ≼ b ，所以 c f( b ) ， 即f( a ) f( b ) ，于是f( a ) R f( b ) 。 故f是保序的 。 对于 b , d  A ， b ∨ d= a f( b ∨ d)=f( a)=A f( b ) ∪ f ( d)=  b , e  ∪  d , e  =  b , d , e  f( b ∨ d)≠f( b ) ∪ f ( d) f不是格同态 。 但是 ， 当f是格同构时 ， 定理 8 . 1 . 7的逆成立

第8章格与布尔代数 定理8.1.8设<X1,≤>和<X2,≤2>是格，<X1,V1,∧1>和<X2, V2,∧2>是它们导出的代数系统。f是X,到X的双射，则∫是 <X,V1,∧>到<X2,V2,∧2>的格同构的充分必要条件是 Va,beX1,a≤1b台a)≤b) 证明：设是<X,V1,个>到<X2,V2,个2>的格同构，下证 Va,b∈X1,a≤b台fa)≤b) 由定理8.1.7可知，Ha,beX,如果a≤，b,必有a)≤2b) 设a@)≤b),由定理8.1.4有a)=a)∧b)=a∧b), 由于f是双射，故a∧，b=a,所以a≤b 这就证明a≤b→a≤b) 设Ha,beX1,a≤，ba)≤b),下证f是<X1,V1,∧>到 <X,V2,∧2>的格同构。 设a∧1b=c,则c≤a,c≤b,c)=a∧b),c)≤a), fc)≤b),故c)≤a)Λb) 设a∧b)=d),则有c)≤a)∧b)=d,即 c)≤d:还有d≤a)和d≤b)。所以有d≤1a和d≤b

第8章 格与布尔代数 定理8.1.8 设X1 ,≼1 和X2 ,≼2 是格，X1 ,∨1 ,∧1 和X2 , ∨2 ,∧2 是它们导出的代数系统。f 是X1到X2的双射，则 f 是 X1 ,∨1 ,∧1  到 X2 ,∨2 ,∧2  的格同构的充分必要条件是 a,bX1，a≼1 bf(a)≼2 f(b) 证明：设f是X1 ,∨1 ,∧1 到X2 ,∨2 ,∧2 的格同构，下证 a,bX1，a≼1 bf(a)≼2 f(b) 由定理8.1.7可知，a,bX1，如果a≼1 b，必有f(a)≼2 f(b) 设f(a)≼2 f(b)，由定理8.1.4有f(a)=f(a)∧2 f(b)=f(a∧1 b)， 由于f是双射，故a∧1 b=a，所以a≼1 b 这就证明a≼1 bf(a)≼2 f(b) 设a,bX1，a≼1 bf(a)≼2 f(b)，下证 f 是X1 ,∨1 ,∧1 到 X2 ,∨2 ,∧2 的格同构。 设a∧1 b=c，则c≼1 a，c≼1 b，f(c)=f(a∧1 b)，f(c)≼2 f(a)， f(c)≼2 f(b)，故 f(c)≼2 f(a)∧2 f(b)。 设f(a)∧2 f(b)=f(d)，则有f(c)≼2 f(a)∧2 f(b)=f(d)，即 f(c)≼2 f(d)；还有f(d)≼2 f(a)和f(d)≼2 f(b)。所以有d≼1 a和d≼1 b