
矢量场的矢量线 例1求矢量场A=x2a+xya,+2a,的矢量线方程 [解]:矢量线应满足的微分方程为 dx dy dz x-y yz xdx ydy dx dy x2-y2=c x-v Z=C,x dx dz c,和c2是积分常数。 lexu@mailxidian.edu.cn
矢量场的矢量线 例 1 求矢量场 A =xy 2 ax +x 2y ay +zy 2 a z的矢量线方程 。 [ 解 ]: 矢量线应满足的微分方程为 y z dz x y dy xy dx 2 2 2 d d y y y d d 2 2 xdx y dy x y dy xy dx 2 2 2 2 1 x y c z cx y z dz xy dx 2 2 2 z cx c 和 c 是积分常数 dx dz x z lexu@mail.xidian.edu.cn 11 xy y z c1和 c x z 2是积分常数
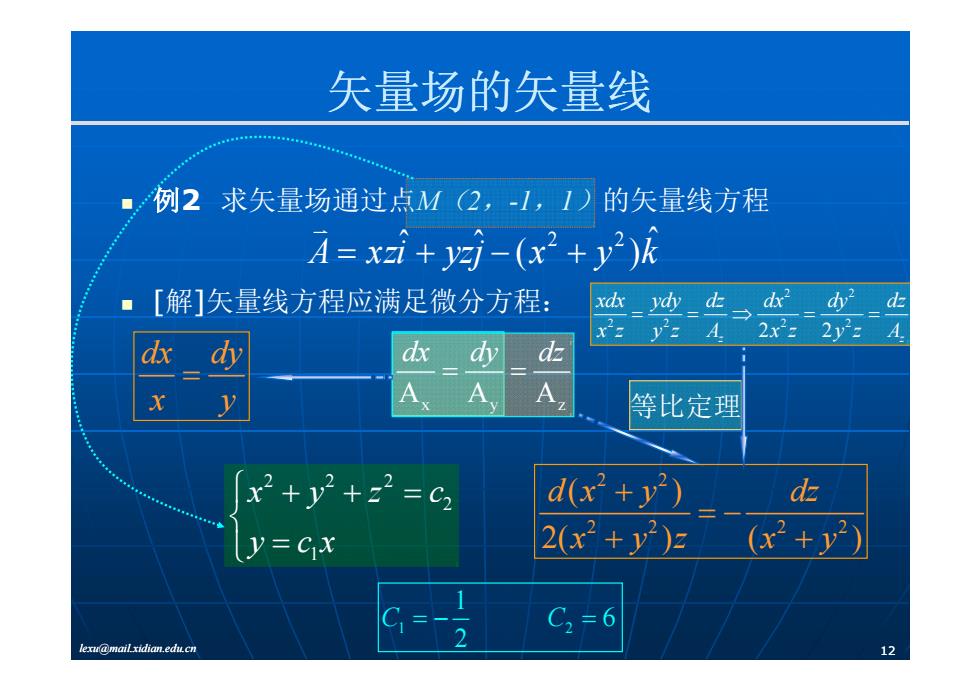
矢量场的矢量线 ■例2求矢量场通过点M(2,-1,1)的矢量线方程 A=xzi+yzj-(x2+y2)k ◆ [解]矢量线方程应满足微分方程: == d2d x'y'A. 2x22y24 dx dy dx dy d A A A 等比定理 x2+y2+z2=c2 d(x2+y2) d y=Cx 2x2+y2) (x2+y2) C=-2 C2=6 lexu@mail xidian.edu.cn 12
矢量场的矢量线 例 2 求矢量场通过点 求矢量场通过点 M (2 ,-1 , 1 )的矢量线方程 A xzi yzj x y k ˆ ( ) ˆ ˆ 2 2 [ 解 ]矢量线方程应满足微分方程: y j ( y ) d d ddd 2 2 22 2 2 2 2 z z xdx ydy dz dx dy dz x z yz A xz yz A AAA xyz dx dy dz 等比定理 dx dy x y 2 2 d x( ) y dz 2 22 2 x y z c 22 22 ( ) 2( ) ( ) y x yz x y 2 1 y y cx lexu@mail.xidian.edu.cn 12 1 2 1 6 2 C C

数量场的等值面与等值线 数量场 。 数量场中各点处的数量是位置的函数,在直角 坐标系中,是点坐标,y,的函数,即: u=u(x,y,z) ·Note1:数量场可用一个数性函数来表示; ·Note2:.场存在的空间即为其定义域; ·Note3:函数单值、连续且有一阶连续偏导 lexu@mail xidian.edu.cn 13
数量场的等值面与等值线 数量场 • 数量场中各点处的数量 u是位置的函数 ,在直角 坐标系中,是点坐标 x , y , z的函数,即: • Note1:数量场可用 一个数性函数来表示; u u ( x , y , z ) • Note1:数量场可用 个数性函数来表示; • Note2:场存在的空间即为其定义域 ; • Note3:函数单值、连续且有一阶连续偏导 lexu@mail.xidian.edu.cn 13