
第七讲 §3.逆矩阵 一逆矩阵 定义8.设A为n阶方阵,如果有一个n阶方阵B, 使 AB=BA三E 则称矩阵A是可逆的,并把矩阵B称为A的逆矩阵A的 逆记之为A1
第七讲 §3.逆矩阵 一.逆矩阵 定义8. 设 A 为 n 阶方阵,如果有一个 n 阶方阵 B, 使 AB = BA = E, 则称矩阵 A 是可逆的,并把矩阵 B 称为 A 的逆矩阵.A的 逆记之为A-1

二. 逆矩阵是唯一的 证明:设B和C都是A的逆矩阵,则 B=BE=B (AC) =(BAC=EC =C 所以A的逆矩阵是唯一的
二. 逆矩阵是唯一的. 证明:设 B 和 C 都是 A 的逆矩阵,则 B = BE = B (AC ) = ( BA ) C = EC = C 所以A的逆矩阵是唯一的
三.逆矩阵的有关定理 定理1.方阵A可逆的充分必要条件是A卡0,且 其中 A A nn 称为A的伴随矩阵.A*中元素是A的所有元素的代数 余子式
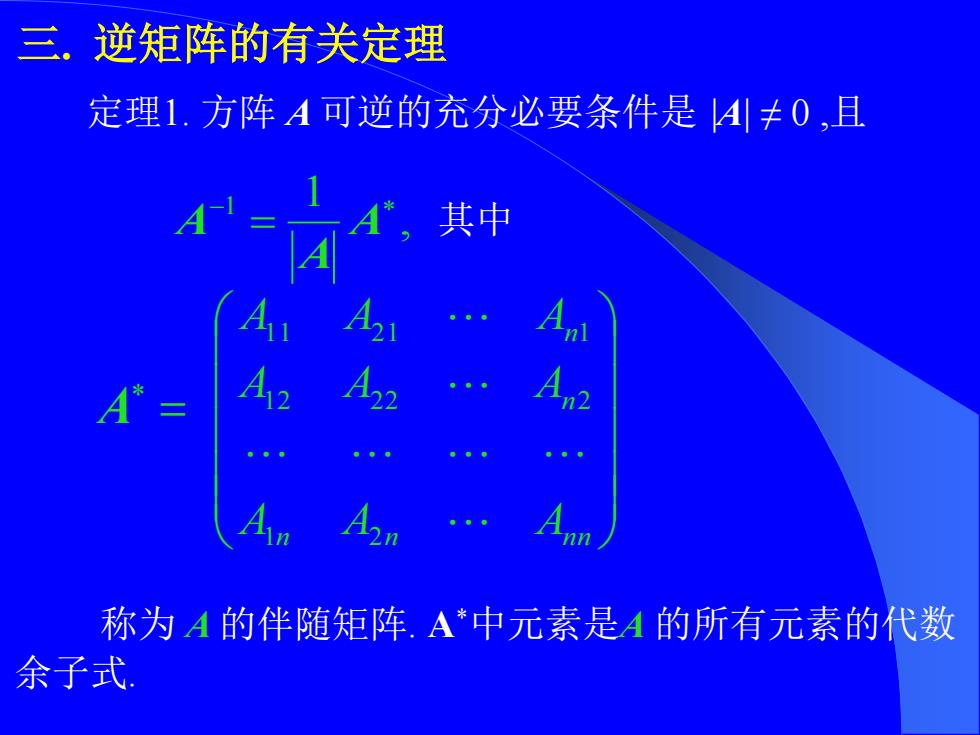
三. 逆矩阵的有关定理 定理1. 方阵 A 可逆的充分必要条件是 |A| ≠ 0 ,且 , −1 1 = A A A 其中 n n n n n n A A A A A A A A A 1 2 1 2 2 2 2 1 1 2 1 1 = A 称为 A 的伴随矩阵. A*中元素是A 的所有元素的代数 余子式

证明: 必要性:因为A可逆, 则有A,使A4=E 1A4=E=1 所以A≠O
证明: 必要性: 因为A可逆, 则有 A −1 ,使 AA = E −1 1 1 = = − A A E 所以 A 0

充分性:由于 a 2 AA= 422 0 n2 .o A -AB
充分性: 由于 = AA n n n n n n n n n n n n A A A A A A A A A a a a a a a a a a 1 2 1 2 2 2 2 1 1 2 1 1 1 2 2 1 2 2 2 1 1 1 2 1 = A A A 0 0 0 0 0 0 = A E