
第二讲 §2.行列式的性质 有了n阶行列式的定义,我们就可以计 算阶行列式,在计算几种特殊行列式的过 程中,发现直接用定义计算是非常麻烦。 当行列式的阶数较高时,计算是士分困 难的,为了简化阶行列式的计算,我们这 节主要研究行列式的性质
第二讲 §2.行列式的性质 有了n阶行列式的定义,我们就可以计 算n阶行列式,在计算几种特殊行列式的过 程中,发现直接用定义计算是非常麻烦。 当行列式的阶数较高时,计算是十分困 难的,为了简化n阶行列式的计算,我们这 一节主要研究行列式的性质

一,转置行列式 把行列式的行换成同序数的列而得到的行列 式称为原行列式的转置行列式。即 a 2 a22 02 0h2 : : : an2 n 称D为D的转置行列式
一 . 转置行列式 ⚫ ⚫ 把行列式的行换成同序数的列而得到的行列 式称为原行列式的转置行列式。即 ⚫ n n n n n n a a a a a a a a a D 1 2 2 1 2 2 2 1 1 1 2 1 = n n n n n n T a a a a a a a a a D 1 2 1 2 2 2 2 1 1 2 1 1 = 称DT为D的转置行列式.

二.行列式的性质 性质1行列式与它的转置行列式 相等 证设 bu d a22 : .: 'nl 0n2 nn b
二.行列式的性质 性质1 行列式与它的转置行列式 相等. ⚫ 证 设 n n n n n n T b b b b b b b b b D 1 2 2 1 2 2 2 1 1 1 2 1 = n n n n n n a a a a a a a a a D 1 2 2 1 2 2 2 1 1 1 2 1 =

显然b,=am(2,广=1,2,,n) 按定义 DT=>(1)bip b2pabnp =∑(-1ap1ap2…apm 由此性质可知,行列式的行与列具有相司 的地位,行列式的性质凡是对行成立的对列也 同样成立,反之亦然
⚫ 由此性质可知,行列式的行与列具有相同 的地位,行列式的性质凡是对行成立的对列也 同样成立,反之亦然。 ij ji 显然 b = a 按定义 (i, j =1,2, ,n) = D ( ) p p p n t n a 1 a 2 a 1 2 = −1 ( ) p p n pn T t D b b b 1 1 2 2 = −1
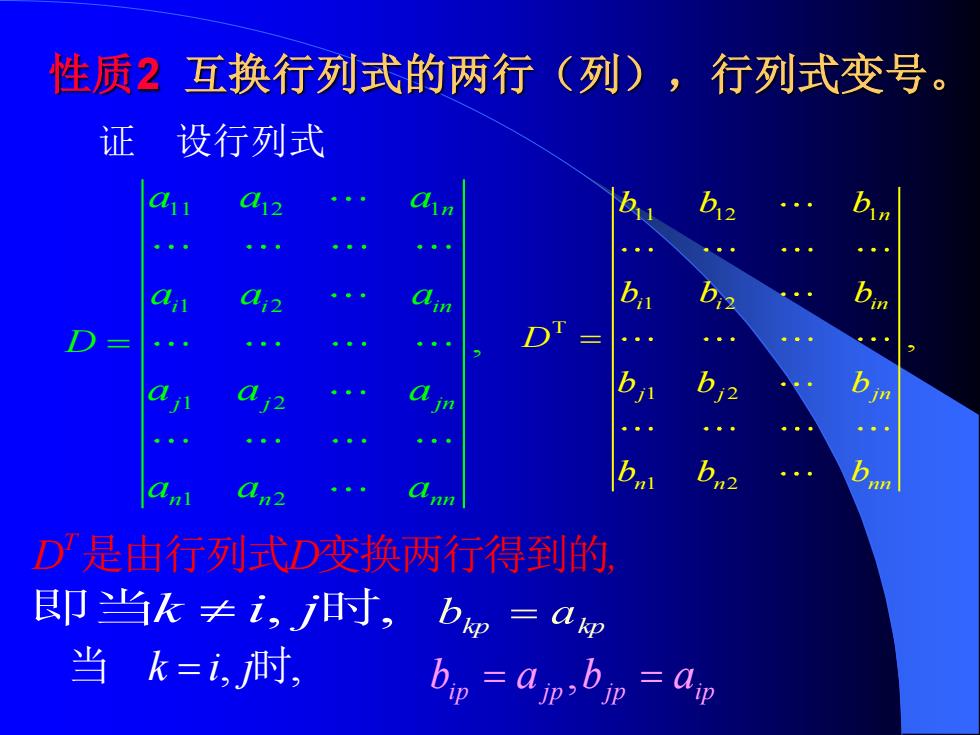
性质2互换行列式的两行(列),行列式变号。 证设行列式 an2 D是由行列式D变换两行得到的 即当k≠i,时,bp=aw 当k=i,时
性质2 互换行列式的两行(列),行列式变号。 bkp = akp i p j p j p i p b = a ,b = a 即当k i, j时, 11 12 1 1 2 1 2 1 2 , n i i in j j jn n n nn a a a a a a D a a a a a a = 证 设行列式 11 12 1 1 2 T 1 2 1 2 , n i i in j j jn n n nn b b b b b b D b b b b b b = T D D , 是由行列式 变换两行得到的 当 k i j = , , 时