
五、方阵的行列式 1、定义 定义6由阶方阵A的元素所构成的行列式 (各元素的位置不变),称为方阵4的行列式, 记作4或detA
五、方阵的 行列式 1、定义 定义6 由n阶方阵A的元素所构成的行列式 (各元素的位置不变),称为方阵A的行列式, 记作 |A| 或 detA

2、运算律 1)A|=1A 2)24=入214 3)川AB=AB
2、运算律 1). ; T A = A 2). A A; n = 3). AB = A B
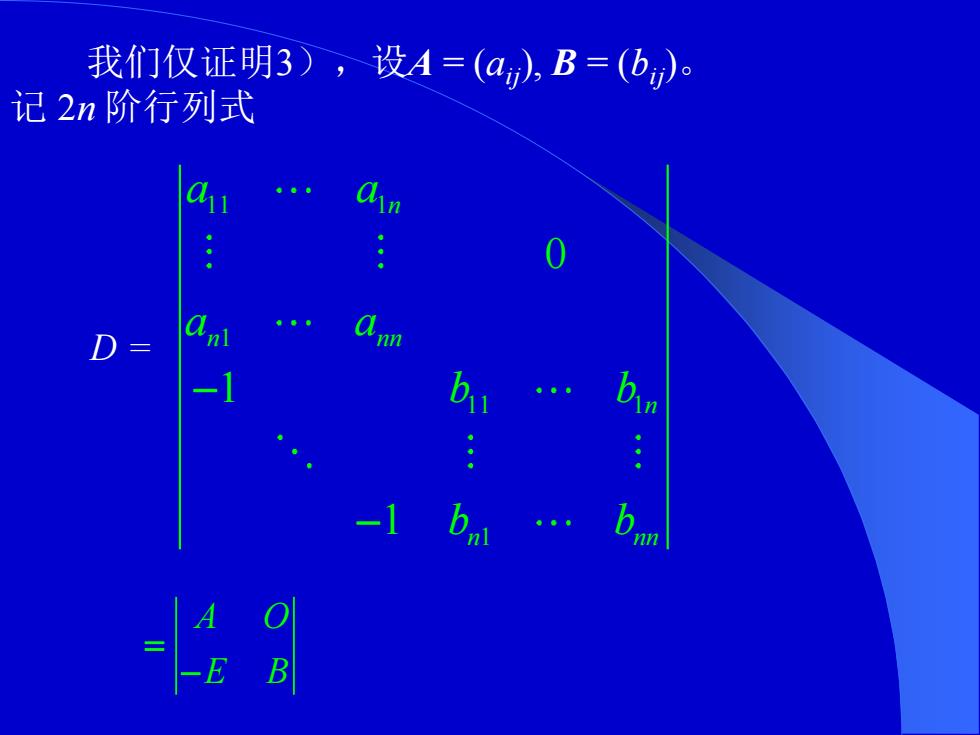
我们仅证明3),设A=(a,B=(b). 记2n阶行列式 -1 b -
我们仅证明3),设A = (aij), B = (bij)。 记 2n 阶行列式 11 1 1 11 1 1 0 1 1 n n nn n n nn a a a a b b b b − − D = A O E B = −

显然,D=AB,而在D中以 b1y乘第1列,b2,乘第2列, bm乘第n列,都加到第n+j列上 (j=1,2,…,n),有 a an am aubu+apba+.+auba a2na,h1ta,b+…+abn a b+ab++ab tg8年t0。t年。t000tt a2 ab+an2h1++anbt… anb+anb ++0b D 1 0 0 0 -1 0 0
显然,D = |A||B| ,而在 D 中以 b1j 乘第 1 列,b2j 乘第 2 列 ,… , bnj 乘第 n 列 , 都加到第 n + j 列上 ( j = 1 , 2 , … , n ) , 有 D= 11 12 1 11 11 12 21 1 1 11 1 12 2 1 21 22 2 21 11 22 21 2 1 21 1 22 2 2 1 2 1 11 2 21 1 1 1 2 2 1 0 0 0 1 0 n n n n n n nn n n n n n n nn n n nn n n nn n n n n n nn nn a a a a b a b a b a b a b a b a a a a b a b a b a b a b a b a a a a b a b a b a b a b a b + + + + + + + + + + + + + + + + + + − − 0 0 0 1−

- 其中C=(ci),cg=a1b+a2bt+amb 故C=AB。 再对D的行作→TayJ=1,2,“,n),有 D-(-iy f d 从而有 D=(-1m-EC=(-1)(-1m川C|=|C|=IAB 于是 AB=AB
0 A C D E = − 其中 C = ( cil ) , cij = ai1b1j+ai2b2j+…+ainbnj , 故 C = AB。 再对 D 的行作 rj ↔ rn+j (j = 1, 2, … , n ),有 0 ( 1) , n E D A C − = − 从而有 D = ( -1 )n |-E||C| = ( -1 )n ( -1 )n | C | = | C | = | AB |。 于是 | AB | = | A | | B |