
R”中的点x=(x,x2,…,xn)与点y=(,y2 第4竟 的距离记作p(x,y)或x-,规定为 px,y)=V(-)2+(x2-y2)》2++(xn-yn》 R”中的点x=(x1,x2,…,xn)与零元O的距离为 x=Vx+x号++x 当n=1,2,3时,x通常记作x. R”中的变元x与定元a满足x-ad→0记作x→a. Rn中点a的δ邻域为 U(a,δ)={xx∈R”,p(x,a)<δ} HIGH EDUCATION PRESS 机动目录上页下页返回结束
的距离记作 中点 a 的 邻域为 ( , , , ) 1 2 n 与点y = y y y 机动 目录 上页 下页 返回 结束 R ( , , , ) 1 2 n n中的点x = x x x 规定为 R ( , , , ) 1 2 n n中的点x = x x x 与零元 O 的距离为 2 2 2 2 1 n x = x + x ++ x 当n =1,2,3时, x 通常记作 x . R x a x − a → 0 n中的变元 与定元 满足 记作 x → a. n R 第4章

猛林女学远销款 \0鞋LRS1Ch 146 武等数兴 第八十讲 多元品教微积 主讲教师:高彦伟 总课时:124
主讲教师:高彦伟 总课时:124 第八十讲 多元函数微积分

二、多元函数的概念 第4章 引例: 圆柱体的体积 V=πr2h,{(r,h)r>0,h>0} 。三角形面积的海伦公式 (p= S=√p(p-a)(p-b(p-c) {(a,b,c)a>0,b>0,c>0,a+b>c} HIGH EDUCATION PRESS 机动目录上页下页返回结束
二、多元函数的概念 引例: • 圆柱体的体积 • 三角形面积的海伦公式 c b a 机动 目录 上页 下页 返回 结束h r 第4章

第4章 定义1.设非空点集DcR”,映射f:D→R 称为定义在D上的n元函数,记作 u=f(x1,x2,…,xn)或u=f(P),P∈D 点集D称为函数的定义域;数集{uu=f(P),P∈D} 称为函数的值域 特别地,当n=2时,有二元函数 z=f(x,y), (x,y)∈DcR2 当n=3时,有三元函数 u=f(x,y,2), (x,y,z)∈DGR3 HIGH EDUCATION PRESS 机动目录上页下页返回结束
定义1. 设非空点集 点集 D 称为函数的定义域 ; 数集 u u = f ( P),P D 称为函数的值域 . 特别地 , 当 n = 2 时, 有二元函数 当 n = 3 时, 有三元函数 映射 称为定义 在 D 上的 n 元函数 , 记作 机动 目录 上页 下页 返回 结束 第4章
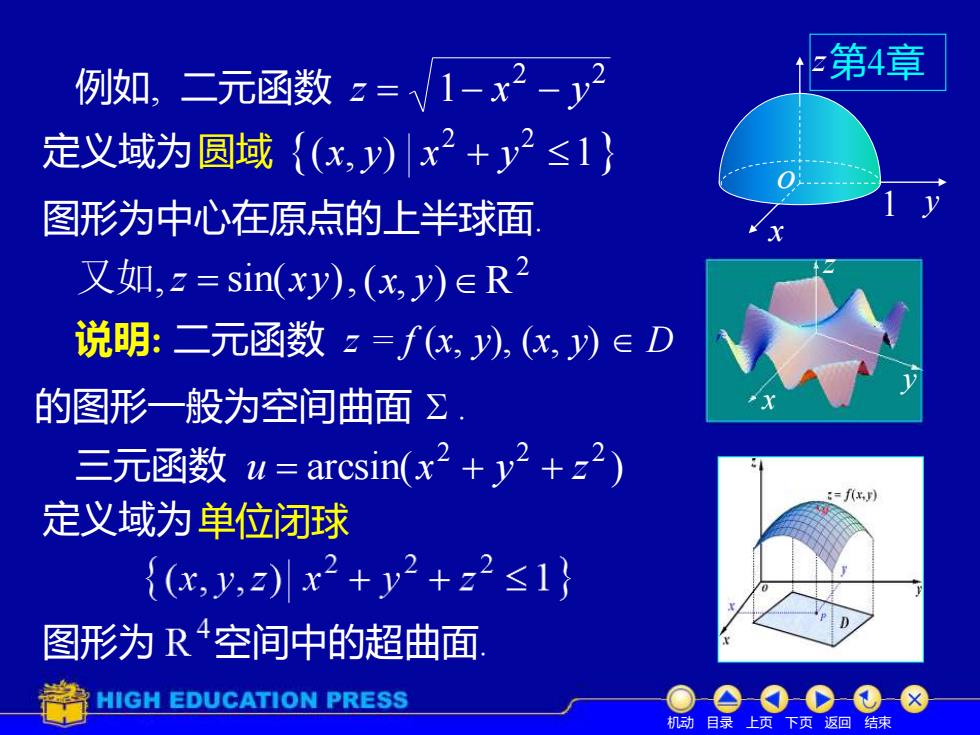
例如,二元函数z=√1-x2-y2 第4章 定义域为圆域{(x,y)x2+y2≤1} 图形为中心在原点的上半球面 又如,2=sin(xy),(x,y)∈R2 说明:二元函数z=f(,y),(x,y)∈D 的图形一般为空间曲面Σ 三元函数u=arcsin(x2+y2+z2) =f() 定义域为单位闭球 {(x,,2)x2+y2+z2≤1} 图形为R4空间中的超曲面 HIGH EDUCATION PRESS 机动目录上页下页返回结束
x z y 例如, 二元函数 2 2 z = 1− x − y 定义域为 ( , ) 1 2 2 圆域 x y x + y 说明: 二元函数 z = f (x, y), (x, y) D 图形为中心在原点的上半球面. 又如,z = sin(xy), 机动 目录 上页 下页 返回 结束 的图形一般为空间曲面 . 1 2 (x, y)R 三元函数 arcsin( ) 2 2 2 u = x + y + z 定义域为 图形为 空间中的超曲面. 单位闭球 x y z o 第4章