
3.1.4、矩阵的转置 王王王王 1、运算规律 (假定所有运算合法,A是矩阵,入R (1)(A)=A (2)(A+B)'=A+B 3(A)=元A(4)(4B)=BA 王王工工王王王 特别(AA,.An1A)=AAn'.4'4 上页 这回
3.1.4、矩阵的转置 1、运算规律 (假定所有运算合法, A B 是矩阵, ) R ( A A ) (1) = (2) ( ) A B A B + = + ( AB B A ) (3) ( A A ) (4) = = ( A A A A A A A A 1 2 1 1 2 1 n n n n − − ) 特别 =

3.1.6、方阵的行列式 2、运算规律 (1)1A=A (2)2A="A (3)4B=4BI=BA (4)4=14" 注 4+B-24+B 上页
3.1.6、方阵的行列式 2、运算规律 (1) A A = n (2) A A = n n (3) AB A B BA = = (4) A A = 注 A B+ ? A B +
补充1、 对称矩阵 定义设的阶方阵,若AI即 =0t 那么称为对称矩阵 如 对称矩阵的特点是: 它的元素以主对角线 为对称轴对应相等. 上页 区回
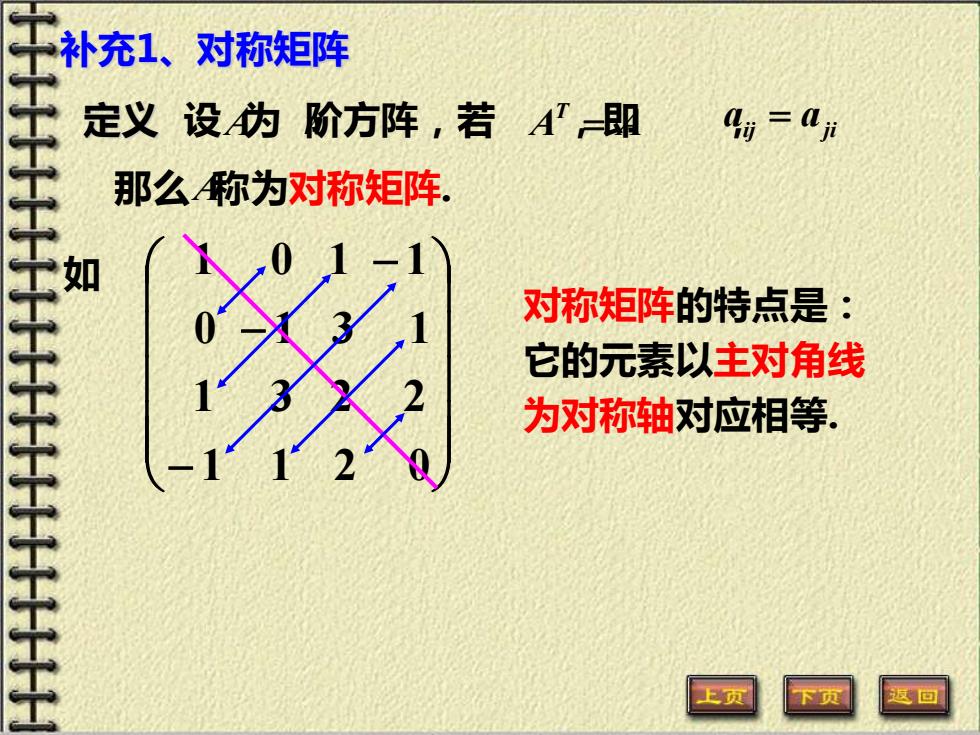
对称矩阵的特点是: 它的元素以主对角线 为对称轴对应相等. − − − 1 1 2 0 1 3 2 2 0 1 3 1 如 1 0 1 1 补充1、对称矩阵 定义 设 A 为 n 阶方阵,若 A A T ,即 = , ij ji a a = 那么 A 称为对称矩阵

补充2、反对称矩阵 A?与即 4=-m 那么称为反对称矩阵 反对称矩阵的主要特点是: 如 主对角线上的元素为0,其余 的元素关于主对角线互为相 反数. 上页 下页 回
0 1 2 1 1 0 5 2 2 5 0 1 1 2 1 0 − − − − − − 定义 A T A A = − ij ji 设 为 n 阶方阵,若 ,即 , a a = − 那么 A 称为反对称矩阵. 反对称矩阵的主要特点是: 主对角线上的元素为0,其余 的元素关于主对角线互为相 反数. 如 补充2、反对称矩阵

第 二 节 逆 矩 阵 1 上页 返回
第二节 逆 矩 阵