(2)静态电阻R反映了某一点时u与i的关系, 而动态电阻R,反映了在某一点u的变化与i的 变化的关系,即u对i的变化率。 (3)对“S”型、“N”型非线性电阻,下倾段 R为负,因此,动态电阻具有“负电阻” 性质
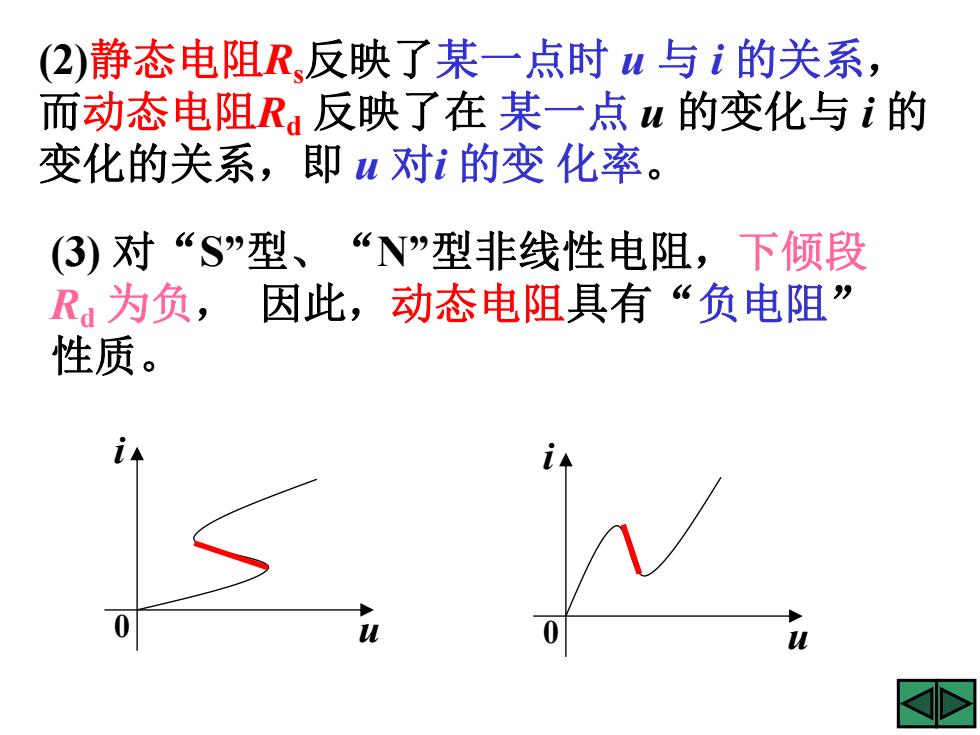
(2)静态电阻Rs反映了某一点时 u 与 i 的关系, 而动态电阻Rd 反映了在 某一点 u 的变化与 i 的 变化的关系,即 u 对i 的变 化率。 (3) 对“S”型、 “N”型非线性电阻,下倾段 Rd 为负, 因此,动态电阻具有“负电阻” 性质。 u i 0 u i 0

四.线性电阻和非线性电阻的区别 例.非线性电阻u=f(0=50i+0.53 sin3t i1=2A u1=100+0.5×8=104V =3 sint-4 sin3t i=2 sin60tA u2=50×2sin60t+0.5×8sin360t =100 sin60t +3 sin60t-sin180t =103 sin60t -sin180t A 出现3倍频 3=10A w3=500+500=1000V i4=0.010A w4=50×0.01+0.5×(0.01)3≈50i4 ①非线性电阻能产生与输入信号不同的频率(变频作用) ②非线性电阻工作范围充分小时,可用工作点处的线性 电阻来近似。 ③齐次性和叠加性不适用于非线性
四. 线性电阻和非线性电阻的区别 例. 非线性电阻 u =f (i) =50 i + 0.5 i3 i1 =2A u1=100+0.58=104V i2=2 sin60tA u2=50 2 sin60t +0.5 8 sin360t =100 sin60t +3 sin60t - sin180t =103 sin60t - sin180t A 出现3倍频 sin3t =3 sint -4 sin3 t i3=10A u3 = 500 + 500 = 1000V i4=0.010A u4 = 50 0.01+ 0.5 (0.01) 3 50 i4 ①非线性电阻能产生与输入信号不同的频率(变频作用) ②非线性电阻工作范围充分小时,可用工作点处的线性 电阻来近似。 ③齐次性和叠加性不适用于非线性

齐次性和叠加性不适用于非线性 i1=2A, u1=104 齐次性不满足 i3=10A, w3=1000V 当i=i1+2(迭加) u=f()=50i+0.53 u=50(i1+i2)+0.5(i1+i2)3 =50i1+0.53+50i2+0.523+1.5i12(i1+2) =w1+w2+1.512(i1+2) ≠儿1+u2 迭加性不满足
齐次性和叠加性不适用于非线性 i1=2 A, u1=104V i3=10A, u3=1000V 齐次性不满足 迭加性不满足 u =50(i1 + i2)+0.5(i1 + i2) 3 =50 i1+ 0.5 i1 3 + 50 i2 +0.5 i2 3 +1.5 i1 i2(i1 + i2) = u1 + u2 +1.5 i1 i2(i1 + i2) u1 + u2 当 i = i1 + i2 ( 迭加 ) u =f (i) =50 i + 0.5 i3
例1 开关 理想二极管 例2 R 子c 0 线性:改变C发生谐振 非线性:改变U 使C发生变化产生谐振
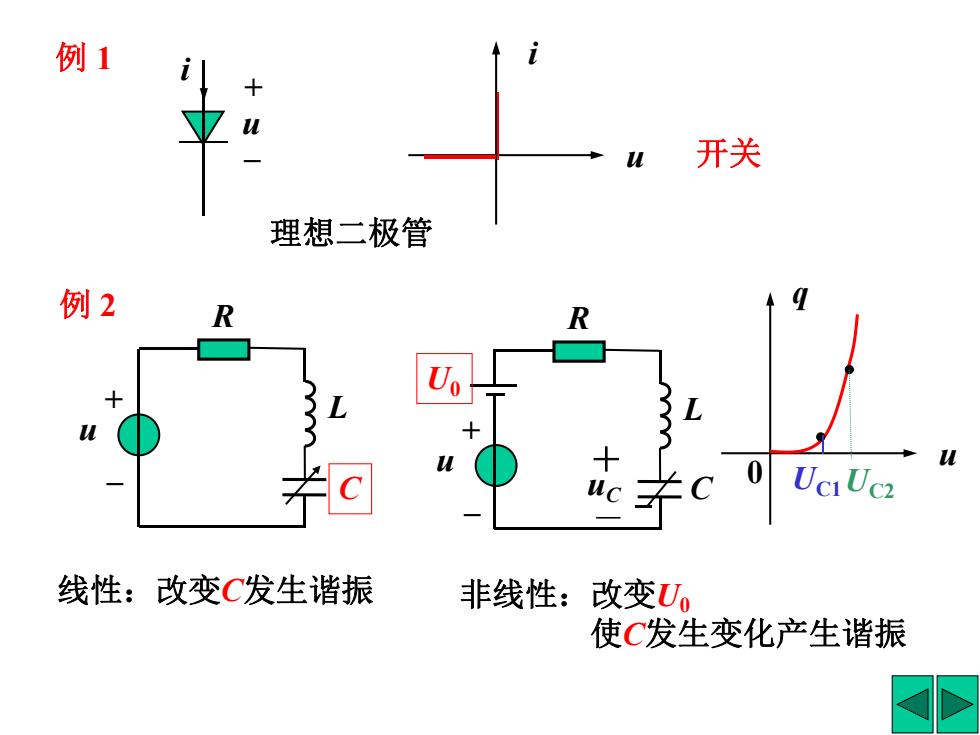
例 1 + _u i u i 理想二极管 开关 例 2 R + _ u L C 线性:改变C发生谐振 非线性:改变U0 使C发生变化产生谐振 u q 0 UC1UC2 R + _ u L C U0 + - uC

17.2非线性电阻的串联、并联电路 一、 非线性电阻的串联 oi +u,() i=in =i u2(i) u=u +u2 u(i) 42(i) 在每一个i下,图解法求 u,将一系列u、i值连成 41() 曲线即得串联等效电阻( 仍为非线性)
17.2 非线性电阻的串联、并联电路 一、非线性电阻的串联 1 2 1 2 u u u i i i u(i) ' u ' u1 在每一个 i 下,图解法求 u ,将一系列 u、i 值连成 曲线即得串联等效电阻 ( 仍为非线性)。 i + + + u ( ) 2 u i ( ) 1 u i i u o ( ) 1 u i ( ) 2 u i ' u1 ' u2 ' i