
(x)sin nxdx 2(0 sin+J1sin 1-cosnz] -2[ -(-1]=nπ 当n=1,3,5, 0 当n=2,4,6,. f(x)=4[§ n+兮n3x*+2k如2-r+ (-0<x<+0,x≠0,±兀,士2π,.)
= − + − 0 0 1 sin d 1 ( 1)sin d 1 nx x nx x 0 1 cos − = n nx 0 1 cos − + n nx n n 1 cos 2 = − n n 1 ( 1) 2 = − − = , 4 n 0 , 当n =1, 3 , 5 , 当n = 2 , 4 , 6 , f x = sin x + 4 ( ) sin 3x + 3 1 − + − + k x k sin(2 1) 2 1 1 (− x + , x 0 , , 2 , ) 机动 目录 上页 下页 返回 结束
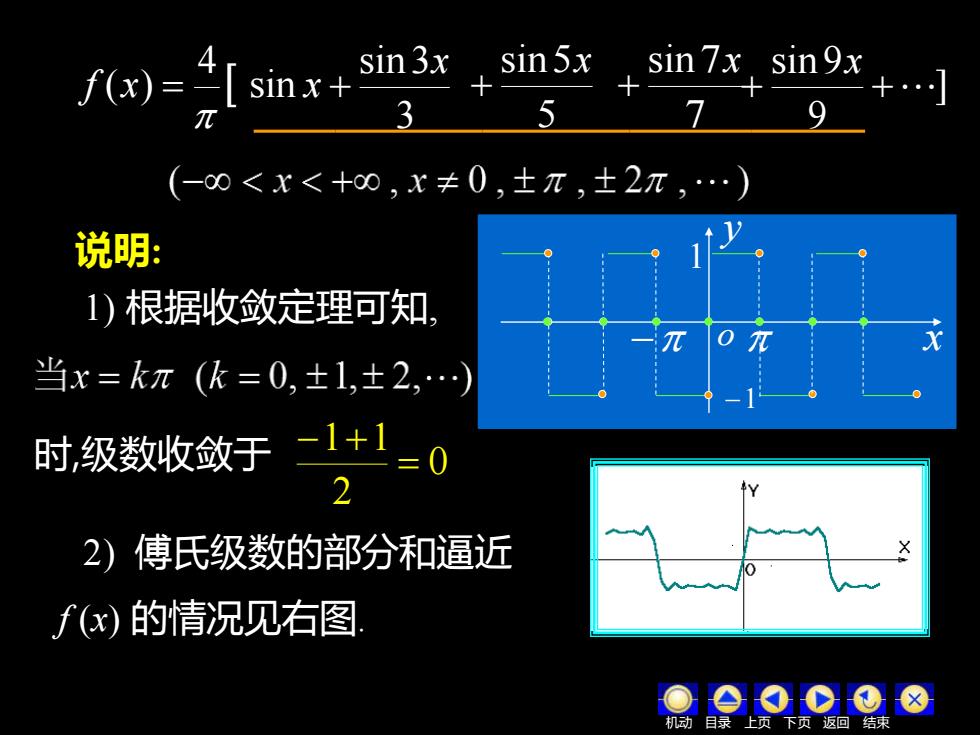
sinx+ in3x,sin5x sin7x,sin9x +] 3 5 (-0<x<+0,x≠0,±π,±2π,.) 说明: 1)根据收敛定理可知, 当x=kπ(k=0,±1,±2,.) 时,级数收敛于 -1+1 -0 2 2)傅氏级数的部分和逼近 f(x)的情况见右图 上页 下页返回结束
7 sin 7x + ] 9 sin 9 + + x 1) 根据收敛定理可知, 时,级数收敛于 0 2 1 1 = − + 2) 傅氏级数的部分和逼近 3 sin 3 sin 4 ( ) x f x = x + 5 sin 5x + o y x −1 − 1 说明: f (x) 的情况见右图. 机动 目录 上页 下页 返回 结束