
一、课程属性简介 课程中文名称: 离散数学 课程编码: ZJH1020140 课程英文名称: Discrete Mathematics 课程类别: 专业基础教育 课程性质: 专业基础核心课程 讲课学时/学分: 64学时/4学分 总学时/学分: 64学时/4学分 实验学时/学分 0学时/0学分 课内实践/学分: 0学时/0学分 计算机科学与技术双语(第 3学期)、 信息管理与信息系 统 (第3学期)、 适用专 开课单位: 计算机与信息工程学院 (开设 软件工程双 学期) (第3学 期)、 网络工程双语 (第3学期) 适用对象。 本科一、二、三本学生 预修课程 高等数学、线性代数 主审人: 制定时 主撰人: 刘霞 周根宝、马学磊 2013.9.16 间: 二、课程教学目标及任务 离散数学,是现代数学的一个重要分支,是计算机科学中基础理论的核心课程。通过本课 程的学习,不仅能为学生学习计算机专业后续课程奠定理论基础,而且能培养学生抽象思维能 力、严格的逻辑推理和创新能力,为将来从事的软、硬件应用开发和理论研究打下坚实的基 础。 本课程要求学生必须理解离散数学主要概念,掌握主要离散结构的构造、性质及其证明 掌握主要推理方法,了解主要模型的应用。 本课程除了重点讲解基本概念和知识外,还特别注重理论推导,注重培养学生的数学抽象 思维能力,提高学生分析问题、解决问题的能力。 三、课程教学内容与教学安排
一、课程属性简介 课程编码: ZJH1020140 课程中文名称: 离散数学 课程英文名称: Discrete Mathematics 课程类别: 专业基础教育 课程性质: 专业基础核心课程 总学时/学分: 64学时/4学分 讲课学时/学分: 64学时/4学分 实验学时/学分: 0学时/0学分 课内实践/学分: 0学时/0学分 开课单位: 计算机与信息工程学院 适用专 业: (开设 学期) 计算机科学与技术双语(第 3学期)、 信息管理与信息系 统 (第3学期)、 软件工程双 语 (第3学 期)、 网络工程双语 (第3学期) 适用对象: 本科一、二、三本学生 预修课程: 高等数学、线性代数 主撰人: 刘霞 主审人: 周根宝、马学磊 制定时 间: 2013.9.16 二、课程教学目标及任务 离散数学,是现代数学的一个重要分支,是计算机科学中基础理论的核心课程。通过本课 程的学习,不仅能为学生学习计算机专业后续课程奠定理论基础,而且能培养学生抽象思维能 力、严格的逻辑推理和创新能力,为将来从事的软、硬件应用开发和理论研究打下坚实的基 础。 本课程要求学生必须理解离散数学主要概念,掌握主要离散结构的构造、性质及其证明, 掌握主要推理方法,了解主要模型的应用。 本课程除了重点讲解基本概念和知识外,还特别注重理论推导,注重培养学生的数学抽象 思维能力,提高学生分析问题、解决问题的能力。 三、课程教学内容与教学安排
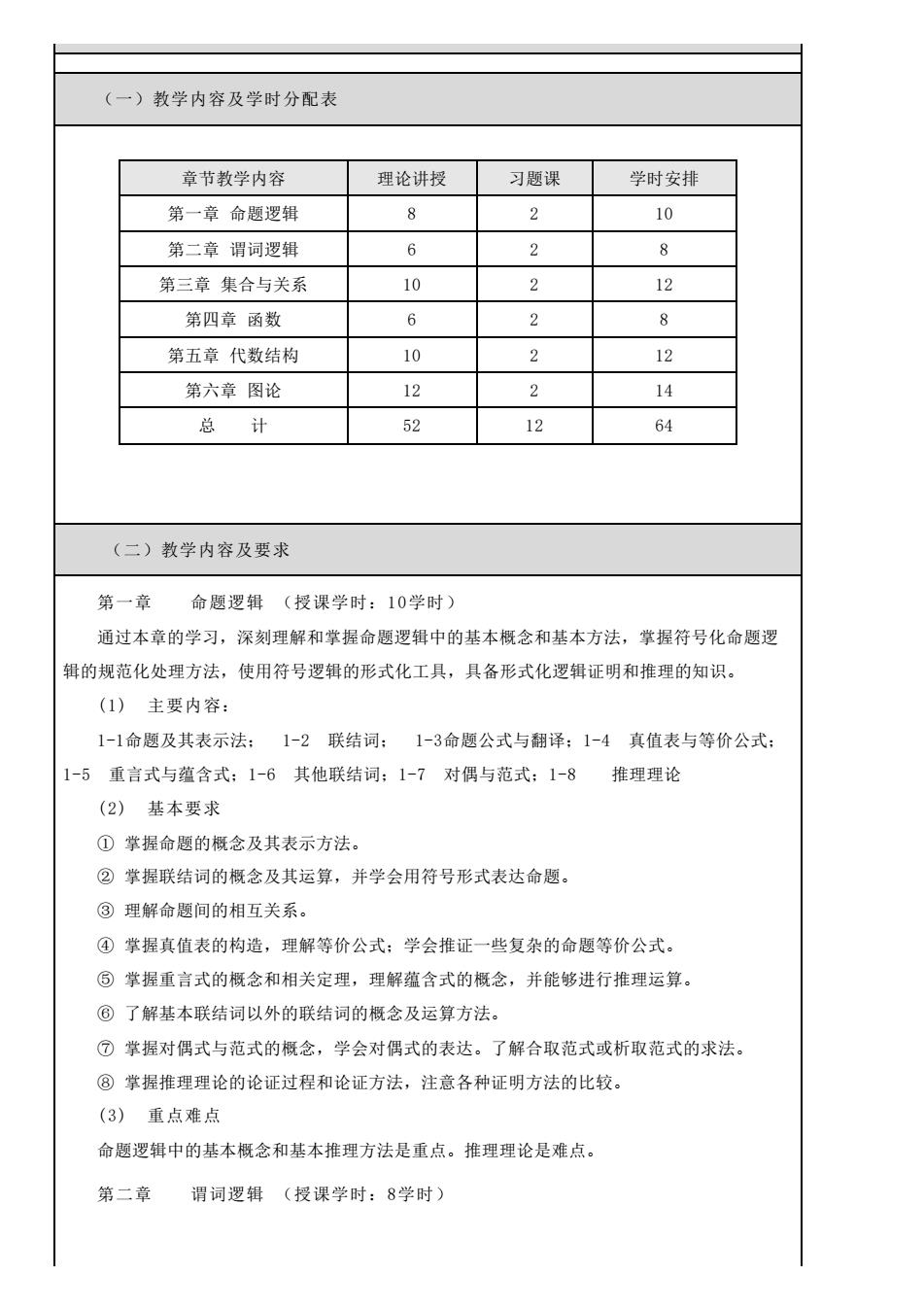
(一)教学内容及学时分配表 章节教学内容 理论讲授 习题课 学时安排 第一章命题逻辑 8 2 10 第二章谓词逻辑 6 2 8 第三章集合与关系 10 2 12 第四章函数 6 2 8 第五章代数结构 10 2 12 第六章图论 12 2 14 总计 52 12 64 (二)教学内容及要求 第一章命题逻辑(授课学时:10学时) 通过本章的学习,深刻理解和掌握命题逻辑中的基本概念和基本方法,掌握符号化命题逻 辑的规范化处理方法,使用符号逻辑的形式化工具,具备形式化逻辑证明和推理的知识。 (1)主要内容: 1-1命题及其表示法:1-2联结词:1-3命题公式与翻译:1-4真值表与等价公式 1-5重言式与蕴含式:1-6其他联结词:1-7对偶与范式:1-8推理理论 (2)基本要求 ①掌握命题的概念及其表示方法。 ②掌握联结词的概念及其运算,并学会用符号形式表达命题。 ③理解命题间的相互关系。 ④掌握真值表的构造,理解等价公式:学会推证一些复杂的命题等价公式。 ⑤掌握重言式的概念和相关定理,理解蕴含式的概念,并能够进行推理运算。 ⑥了解基本联结词以外的联结词的概念及运算方法。 ⑦掌握对偶式与范式的概念,学会对偶式的表达。了解合取范式或析取范式的求法。 ⑧掌握推理理论的论证过程和论证方法,注意各种证明方法的比较。 (3)重点难点 命题逻辑中的基本概念和基本推理方法是重点。推理理论是难点 第二章 谓词逻辑(授课学时:8学时)
(一)教学内容及学时分配表 章节教学内容 理论讲授 习题课 学时安排 第一章 命题逻辑 8 2 10 第二章 谓词逻辑 6 2 8 第三章 集合与关系 10 2 12 第四章 函数 6 2 8 第五章 代数结构 10 2 12 第六章 图论 12 2 14 总 计 52 12 64 (二)教学内容及要求 第一章 命题逻辑 (授课学时:10学时) 通过本章的学习,深刻理解和掌握命题逻辑中的基本概念和基本方法,掌握符号化命题逻 辑的规范化处理方法,使用符号逻辑的形式化工具,具备形式化逻辑证明和推理的知识。 (1) 主要内容: 1-1命题及其表示法; 1-2 联结词; 1-3命题公式与翻译;1-4 真值表与等价公式; 1-5 重言式与蕴含式;1-6 其他联结词;1-7 对偶与范式;1-8 推理理论 (2) 基本要求 ① 掌握命题的概念及其表示方法。 ② 掌握联结词的概念及其运算,并学会用符号形式表达命题。 ③ 理解命题间的相互关系。 ④ 掌握真值表的构造,理解等价公式;学会推证一些复杂的命题等价公式。 ⑤ 掌握重言式的概念和相关定理,理解蕴含式的概念,并能够进行推理运算。 ⑥ 了解基本联结词以外的联结词的概念及运算方法。 ⑦ 掌握对偶式与范式的概念,学会对偶式的表达。了解合取范式或析取范式的求法。 ⑧ 掌握推理理论的论证过程和论证方法,注意各种证明方法的比较。 (3) 重点难点 命题逻辑中的基本概念和基本推理方法是重点。推理理论是难点。 第二章 谓词逻辑 (授课学时:8学时)

通过本章的学习,深刻理解和掌握谓词逻辑的基本概念和基本推理方法。掌握符号化谓词 逻辑的规范化处理方法,具备形式化逻辑证明和推理的知识并解决实际问题。 (1)主要内容: 2-1谓词的概念与表示:2-2命题函数与量词:2-3谓词公式与翻译:2-4变元的约 束:2-5谓词演算的等价式与蕴含式:2-6前束范式:2-7谓词演算的推理理论。 (2)基本要求 ①掌提谓词的概念与表示方法。 ②掌握命题函数、量词的概念。学会用谓词表达式写出命题。 ③掌握谓词公式,学会利用谓词公式翻译命题。 ④了解变元的约束。 ⑤掌握谓词公式的等价和永真的概念,理解谓词演算的一些等价式和蕴含式。 ⑥了解前束范式的概念。 ⑦掌握谓词演算的推理规则,并以大量的例题说明其演算方法。 (3)重点难点 谓词逻辑中的基本概念和基本推理方法是重点。谓词演算的推理理论是难点。 第三章 集合与关系(授课学时:12学时) 通过本章的学习,深刻理解和掌握有关集合和关系的基本概念和基本运算。掌握离散与连 续的关系、集合的操作,将实际例子与合适的集合、关系模型关联起来。 (1)主要内容: 3-1集合的概念和表示法;3-2集合的运算:*3-3包含排斥原理:3-4序偶和笛卡尔 积:3-5关系及其表示:3-6关系的性质:3-7复合关系和逆关系:3-8关系的闭包运算:3 9集合的划分和覆盖:3-10等价关系与等价类:3-11相容关系:3-12序关系。 (2)基本要求 ①掌握集合的概念和表示方法,理解用谓词描述或表达集合的方法。 ②掌握关于集合运算的定义和定理。理解文图。 ③掌握序偶的定义,理解笛卡尔积的表示和运算。 ④理解关系的概念,重点掌握二无关系,以及的它的关系矩阵、关系图。 ⑤掌握关系的一些特殊性质,学会用关系矩阵、关系图去判断关系的性质, ⑥掌握复合关系和逆关系的定义、性质。 ⑦掌握关系的闭包运算的概念、方法。 ⑧理解集合的划分和覆盖。 ⑨掌握等价关系,理解等价类。 ⑩了解相容关系的定义、定理。 ⑩掌握偏序集、链、线序关系、良序关系的要领和性质,理解最大元、最小元的定义
通过本章的学习,深刻理解和掌握谓词逻辑的基本概念和基本推理方法。掌握符号化谓词 逻辑的规范化处理方法,具备形式化逻辑证明和推理的知识并解决实际问题。 (1) 主要内容: 2-1 谓词的概念与表示;2-2 命题函数与量词;2-3 谓词公式与翻译;2-4 变元的约 束;2-5 谓词演算的等价式与蕴含式;2-6 前束范式;2-7 谓词演算的推理理论。 (2) 基本要求 ① 掌握谓词的概念与表示方法。 ② 掌握命题函数、量词的概念。学会用谓词表达式写出命题。 ③ 掌握谓词公式,学会利用谓词公式翻译命题。 ④ 了解变元的约束。 ⑤ 掌握谓词公式的等价和永真的概念,理解谓词演算的一些等价式和蕴含式。 ⑥ 了解前束范式的概念。 ⑦ 掌握谓词演算的推理规则,并以大量的例题说明其演算方法。 (3) 重点难点 谓词逻辑中的基本概念和基本推理方法是重点。谓词演算的推理理论是难点。 第三章 集合与关系(授课学时:12学时) 通过本章的学习,深刻理解和掌握有关集合和关系的基本概念和基本运算。掌握离散与连 续的关系、集合的操作,将实际例子与合适的集合、关系模型关联起来。 (1) 主要内容: 3-1 集合的概念和表示法;3-2集合的运算;*3-3 包含排斥原理;3-4序偶和笛卡尔 积;3-5关系及其表示;3-6 关系的性质;3-7 复合关系和逆关系;3-8关系的闭包运算;3- 9集合的划分和覆盖;3-10等价关系与等价类;3-11相容关系;3-12序关系。 (2) 基本要求 ① 掌握集合的概念和表示方法,理解用谓词描述或表达集合的方法。 ② 掌握关于集合运算的定义和定理。理解文图。 ③ 掌握序偶的定义,理解笛卡尔积的表示和运算。 ④ 理解关系的概念,重点掌握二无关系,以及的它的关系矩阵、关系图。 ⑤ 掌握关系的一些特殊性质,学会用关系矩阵、关系图去判断关系的性质。 ⑥ 掌握复合关系和逆关系的定义、性质。 ⑦ 掌握关系的闭包运算的概念、方法。 ⑧ 理解集合的划分和覆盖。 ⑨ 掌握等价关系,理解等价类。 ⑩ 了解相容关系的定义、定理。 ⑩ 掌握偏序集、链、线序关系、良序关系的要领和性质,理解最大元、最小元的定义

(3) 重点难点 关系及关系的运算、等价关系、相容关系、序关系是重点,关系的闭包运算、等价关系 等价类、偏序集是难点。 第四章 函数(授课学时:8学时) 通过本章的学习,深刻理解离散与连续的函数、关系、集合的概念,掌握集合基数的概 念。 (1)主要内容: 4-1函数基本概念:4-2逆函数和复合函数:44基数的概念:4-5可数集与不可数集:4 6基数的比较 (2)基本要求 ①掌握函数的概念以及满射、入射、双射的概念。 ②掌握逆函数、复合函数的定义和性质。 ③掌提基数的概念,学会构造映射函数 ④掌握有限集、可数集与不可数集的概念与证明方法。 ⑤了解基数比较的概念与方法。 (3)重点难点 函数的概念、逆函数和复合函数、集合基数的概念、可数集与不可数集的概念是难点,集 合基数的概念是难点。 第五章代数结构(授课学时:12学时) 通过本章的学习,深刻理解和掌握有关代数系统结构,掌握群、环、域等代数系统基本结 构和基本运算。 (1)主要内容: 5-1代数系统的引入:5-2运算及其性质:5-3半群:5-4群与子群:5-5阿贝尔群和循 环群:*5-6置换群与伯恩赛德定理:5-7陪集与拉格朗日定理:5-8同态与同构:5-9环与 绿。 (2)基本要求 ①了解一般代数系统的概念 ②掌握二元运算的概念和性质。注意运算符号的表达 ③掌握半群的概念和独异点的概念和半群的性质。 ④学握群与子群的定义,注意与半群的不同点,理解有关群的一些性质 ⑤掌握阿贝尔群和循环群的概念性质。 ⑥了解陪集的定义与拉格朗日定理。 ⑦掌握同态与同构的定义及相关定理。 ⑧了解环、整环、域的概念及性质。了解同态象的概念。 (3)重点难点
(3) 重点难点 关系及关系的运算、等价关系、相容关系、序关系是重点,关系的闭包运算、等价关系、 等价类、偏序集是难点。 第四章 函数 (授课学时:8学时) 通过本章的学习,深刻理解离散与连续的函数、关系、集合的概念,掌握集合基数的概 念。 (1) 主要内容: 4-1 函数基本概念;4-2逆函数和复合函数;4-4基数的概念;4-5可数集与不可数集;4- 6基数的比较 (2) 基本要求 ① 掌握函数的概念以及满射、入射、双射的概念。 ② 掌握逆函数、复合函数的定义和性质。 ③ 掌握基数的概念,学会构造映射函数。 ④ 掌握有限集、可数集与不可数集的概念与证明方法。 ⑤ 了解基数比较的概念与方法。 (3) 重点难点 函数的概念、逆函数和复合函数、集合基数的概念、可数集与不可数集的概念是难点,集 合基数的概念是难点。 第五章 代数结构(授课学时:12学时) 通过本章的学习,深刻理解和掌握有关代数系统结构,掌握群、环、域等代数系统基本结 构和基本运算。 (1) 主要内容: 5-1 代数系统的引入;5-2运算及其性质;5-3 半群;5-4群与子群;5-5阿贝尔群和循 环群;*5-6 置换群与伯恩赛德定理;5-7陪集与拉格朗日定理;5-8同态与同构;5-9环与 域。 (2) 基本要求 ① 了解一般代数系统的概念。 ② 掌握二元运算的概念和性质。注意运算符号的表达。 ③ 掌握半群的概念和独异点的概念和半群的性质。 ④ 掌握群与子群的定义,注意与半群的不同点,理解有关群的一些性质。 ⑤ 掌握阿贝尔群和循环群的概念性质。 ⑥ 了解陪集的定义与拉格朗日定理。 ⑦ 掌握同态与同构的定义及相关定理。 ⑧ 了解环、整环、域的概念及性质。了解同态象的概念。 (3) 重点难点

同构和同态、群、环、域的概念及运算是重点,代数结构、同构和同态的概念。 第六章图论(授课学时:14学时) 通过本章的学习,深刻理解和掌握图的有关概念和表示。掌握计算中使用图和树构建的模 型:了解图和树相关的数据结构、算法和计数。 (1)主要内容 7-1图的基本概念:7-2路和回路:7-3图的矩阵表示:7-4欧拉图与汉密尔顿图: *7-5平面图:*7-6对偶图与着色:7-7树与生成树:7-8根数及其应用。 (2)基本要求 ①掌握图的概念,了解图的同构。 ②理解路与回路的概念,了解有关连通图的性质。 ③掌握图的矩阵表示方法。 ④掌握欧拉图的概念和性质,了解汉密尔顿图的概念和性质。 ⑤了解平面图,掌握欧拉定理。 ⑥了解对偶图与若色理论。 ⑦掌握树与生成树的概念及性质 ⑧了解根树的定义及应用。 (3)重点难点 图、路、图的矩阵表示、树与生成树是重点,树与生成树是难点。 (三)课程考核与成绩评定 1.考核方式:考试,笔试,闭卷。 2.成绩评定:卷面成绩占总成绩70%,平时学生出勤占5%,项目考核占5%,学生期中考试成续 占20%。 (四)推荐教材和教学参考书 1.教材: 左孝凌等·离散数学·上海:上海科学技术文献出版社 2.参考书: [1门屈婉玲,耿素云,张立昂·离散数学·高等教育出版社,2008 [2]段禅伦等·离散数学·内蒙古:内蒙古大学出版社,1997 [3]徐洁磐·离散数学导论·北京:人民教育出版社,1982
同构和同态、群、环、域的概念及运算是重点,代数结构、同构和同态的概念。 第六章 图论 (授课学时:14学时) 通过本章的学习,深刻理解和掌握图的有关概念和表示。掌握计算中使用图和树构建的模 型;了解图和树相关的数据结构、算法和计数。 (1) 主要内容: 7-1 图的基本概念;7-2 路和回路;7-3图的矩阵表示; 7-4欧拉图与汉密尔顿图; *7-5 平面图; *7-6对偶图与着色;7-7树与生成树; 7-8根数及其应用。 (2) 基本要求 ① 掌握图的概念,了解图的同构。 ② 理解路与回路的概念,了解有关连通图的性质。 ③ 掌握图的矩阵表示方法。 ④ 掌握欧拉图的概念和性质,了解汉密尔顿图的概念和性质。 ⑤ 了解平面图,掌握欧拉定理。 ⑥ 了解对偶图与着色理论。 ⑦ 掌握树与生成树的概念及性质。 ⑧ 了解根树的定义及应用。 (3) 重点难点 图、路、图的矩阵表示、树与生成树是重点,树与生成树是难点。 (三)课程考核与成绩评定 1.考核方式:考试,笔试,闭卷。 2.成绩评定:卷面成绩占总成绩70%,平时学生出勤占5%,项目考核占5%,学生期中考试成绩 占20%。 (四)推荐教材和教学参考书 1.教材: 左孝凌等·离散数学·上海:上海科学技术文献出版社 2.参考书: [1]屈婉玲,耿素云,张立昂·离散数学·高等教育出版社,2008 [2] 段禅伦等·离散数学·内蒙古:内蒙古大学出版社,1997 [3] 徐洁磐·离散数学导论·北京:人民教育出版社,1982