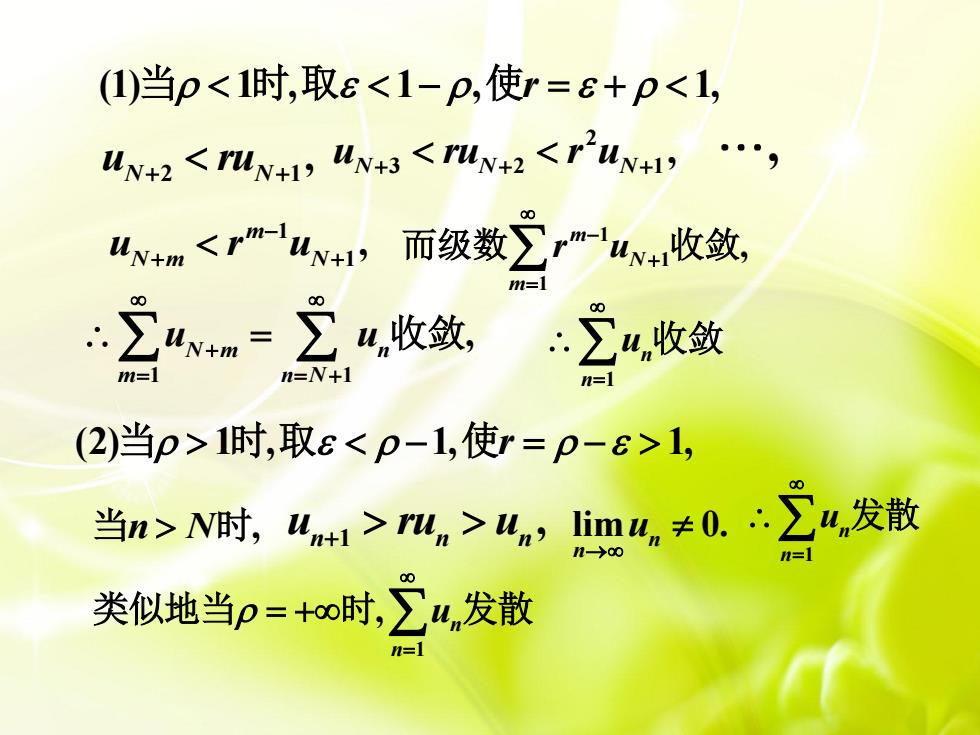
(1)当p<1时,取8<1-p,使r=+p<1, UN+2 <rUN4 HN43<FuN+2<r'UN+ 山+m<lv+1,而级数∑"山收敛, m= 立4n=立u收敛,4收敛 (2)当p>1时,取ε<p-1,使r=p-8>1, 当m>N时1>m,>么,吧%,空,发散 类似地当p=+oo时,∑4n发散 n=
(1) 1 , 1 , 1, 当 时 取 使r (2) 1 , 1, 1, 当 时 取 使r 1 1 , m u r u N m N 2 1 , u ru N N 2 3 2 1 , u ru r u N N N , 1 1 1 , m N m r u 而级数 收敛 1 1 , N m n m n N u u 收敛 当n N 时, 1 , u ru u n n n lim 0. n n u 1 n n u 收敛 1 n n u 发散 1 , n n u 类似地当 时 发散

比值审敛法的优点:不必找参考级数. 适应于w,中含有n:或关于的若干项连乘(除)的形式. 两点注意: 1当p=1时比值审敛法失效 级数 发散, 例 n=1 (p=1) 0 收敛
比值审敛法的优点:不必找参考级数. 两点注意: 1 2 1 1 , ( 1) 1 , n n n n 级数 发散 例 级数 收敛 1. 1 ; 当 时比值审敛法失效 ! 适应于u n n n 中含有 或关于 的若干项连乘(除)的形式

2.条件是充分的,而非必要. 蛇,2≥收敛文 lim=p<1 = n-o儿n 例:,=2+)3 2 2 ·级数∑ 号2+(-1)收敛, 2 =1 n=l 但1 2+(-1)+1 1 4n2(2+(-1)") n→c0 6 3 1ima2+1= ÷lim=iman不存在 n→o n-→oo儿n l→00
2 ( 1) 3 , 2 2 n n n n n u v 例 1 1 2 ( 1) , 2 n n n n n u 级数 收敛 1 1 2 ( 1) , 2(2 ( 1) ) n n n n n u a u 但 2 1 lim , 6 n n a 2 1 3 lim , 2 n n a 1 lim lim . n n n n n u a u 不存在 2.条件是充分的,而非必要. 1 ,( 0) n n n u u 由 收敛 1 lim 1 n n n u u