电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第三章 分离变量法（2/4）

Φ”+Φ=0 (2)求解固有值问题 Φ(0+2π)=Φ(0)》 1)1<0 D"+Φ=0x2+九=0x=±√-元 ↓ Φ(O)=Ae0+BeF0 Φ(8+2π)=Φ(0) →A=0,B=0〉Φ(8)=0 2)1=0 Φ"+=0〉x2=0→x=0(重根) ↓ Φ(O)=A+B0 →取任意值，B=0→Φ，()=C Φ(0+2π)=Φ(0)

(2) 求解固有值问题                    2 0 1) λ < 0       0 2 x    0 x    ( ) Ae Be                 2    A B   0, 0   ( ) 0  2) λ = 0       0 2 x  0 x  0( ) 重根    ( )   A B        2    A B 取任意值, 0  0  ( )=  C

Φ”+Φ=0 Φ(0+2π)=Φ(0)》 3)入>0 Φ”+Φ=0〉x2+元=0→x=±iW万 Q Φ(e)=Acos√0+Bsin√B→D(O)=Acos B0+BsinB0 Φ(0+2π)=Φ(0) →Bn=n,(n=1,2,）→n=7,(n=1,2, Φ(0)=Acos√n0+Bsin√几0 Φ，(O)=4,cos n0+B sin n0

                   2 0 3) λ > 0       0 2 x    0 x i       ( ) cos sin    A B        2       ( ) cos sin    A B ,( 1,2, ) n   n n 2 ,( 1,2, ) n   n n    ( ) cos sin    A B    n n n ( ) cos sin    A n B n

Φ”+Φ=0 元=0→Φ(0)=C Φ(0+2π)=Φ(0) 入n=n2,n=1,2,)Φ，(0)=A,cosn0+B.sin n0 固有值：2n=n2,(n=0,1,2,… 固有函数：Φn(0)=A,cosn0+B.sin n0,(n=0,1,2…)

                   2 0 2 ,( 1,2, ) n   n n    n n n ( ) cos sin    A n B n 0   0  ( )=  C 固有值: 2 ,( 0,1,2, ) n   n n 固有函数： ( ) cos sin ,( 0,1,2 )     n n n    A n B n n

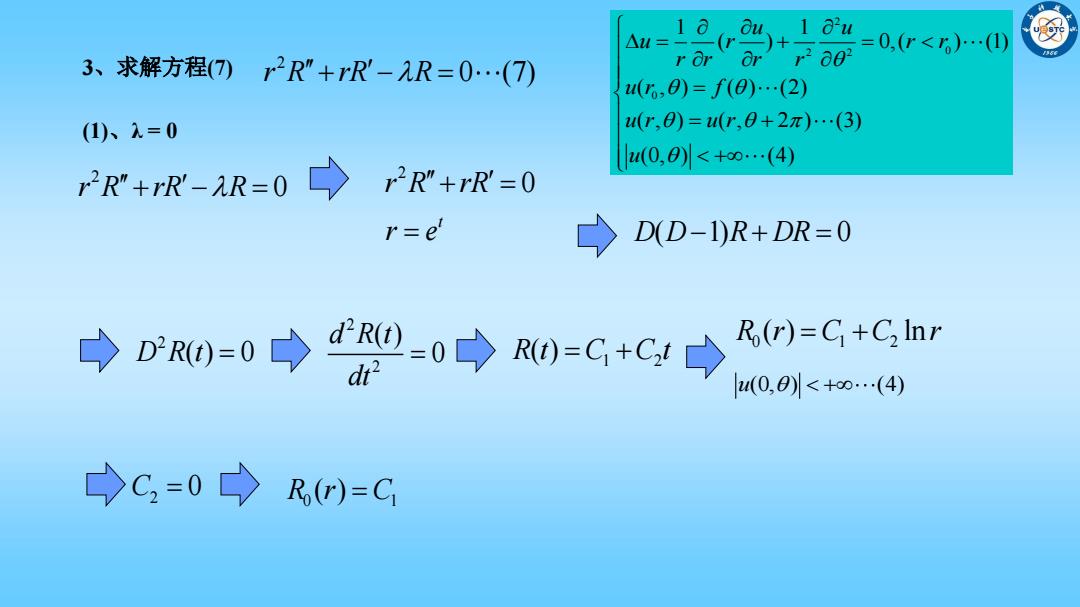
1oau、,1a'4 r or or r2 002 =0,<6)0 3、求解方程(7)2R"+rR-R=0(⑦) ,0)=f(0)…(2) (1)、1=0 (r,0)=u(r,0+2π)…(3) r2R+R-R=0→2R"+rR=0 u(0,0)<+0…(4) r=e" → D(D-1)R+DR=0 →D0=0→2-0今0=C+G→ Ro(r)=C+C2 Inr (0,0)<+oo…(4) →C=0→R)=C

3、求解方程(7) 2 r R rR R       0 (7) 2 2 2 0 0 1 1 ( ) 0,( ) (1) ( , ) ( ) (2) ( , ) ( , 2 ) (3) (0, ) (4) u u u r r r r r r r u r f u r u r u                                (1)、λ = 0 2 r R rR R       0 2 r R rR     0 t r e  D D R DR ( 1) 0    2 D R t( ) 0  2 2 ( ) 0 d R t dt  u(0, ) (4)    0 1 R r C ( )  1 2 R t C C t ( )   0 1 2 R r C C r ( ) ln   2 C  0