向量的数乘 几何向量乘以标量后,其几何 长度改变相应的倍数,而方向 不变。如果乘数为负数,则向 量的方向反转,但仍与原向量 共线。用代数方法表示时,设 乘数λ为标量 V Av V= V2 则 Av= 2N2 2w3 。 经过数乘后的向量几何长度也 为原几何长度的数乘: 2w=V(y)2+(2y2)2+(2)2=v
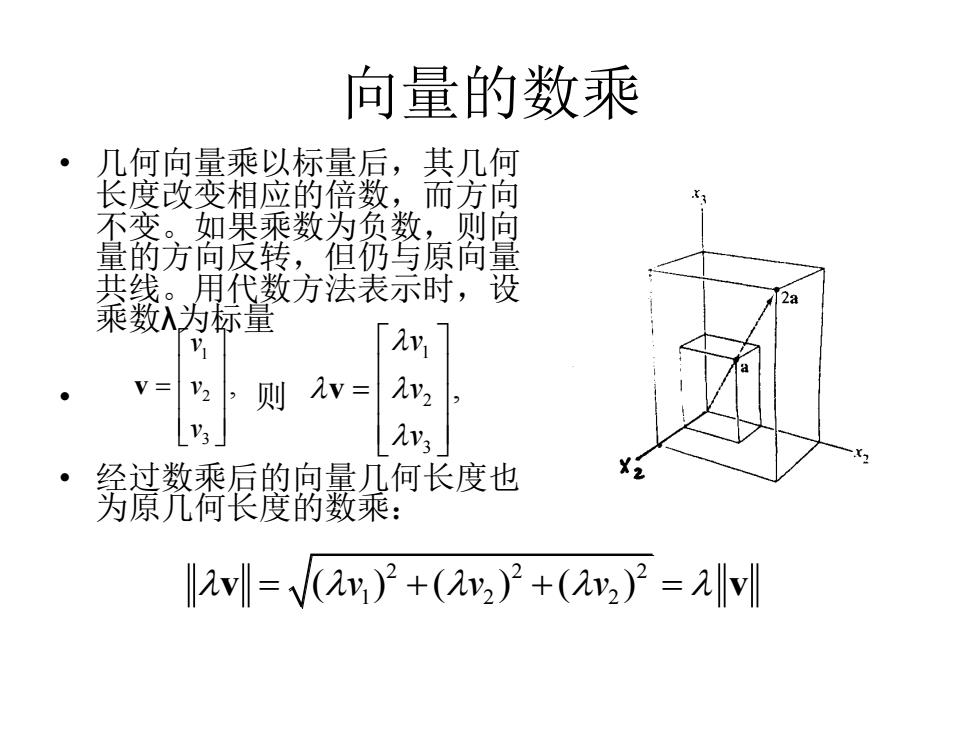
向量的数乘 • 几何向量乘以标量后,其几何 长度改变相应的倍数,而方向 不变。如果乘数为负数,则向 量的方向反转,但仍与原向量 共线。用代数方法表示时,设 乘数λ为标量 • 则 • 经过数乘后的向量几何长度也 为原几何长度的数乘: 1 2 3 , v v v = v 1 2 3 , v v v = v 222 1 2 2 v v = + + = ( ) ( ) ( ) v v v
单位向量和方向余弦 。 单位向量指几何长度为一的向量。V 的单位向量通常写成v0,V。=vv, 平面单位向量的两个分量是该向量在 xy轴上的投影,也就是该向量与xy Cosy 轴夹角的方向余弦。对于三维向量也 是如此,因此单位向量0的各个分量 cos 标志了该向量在坐标系中的方向。 只要x,y,z是直角坐标系,V0与各坐标 Co 轴的夹角就一定满足; cosa vvo=[cosa cos B cosy] cos B cos2a+cos2 B+cosy2=1 COSY
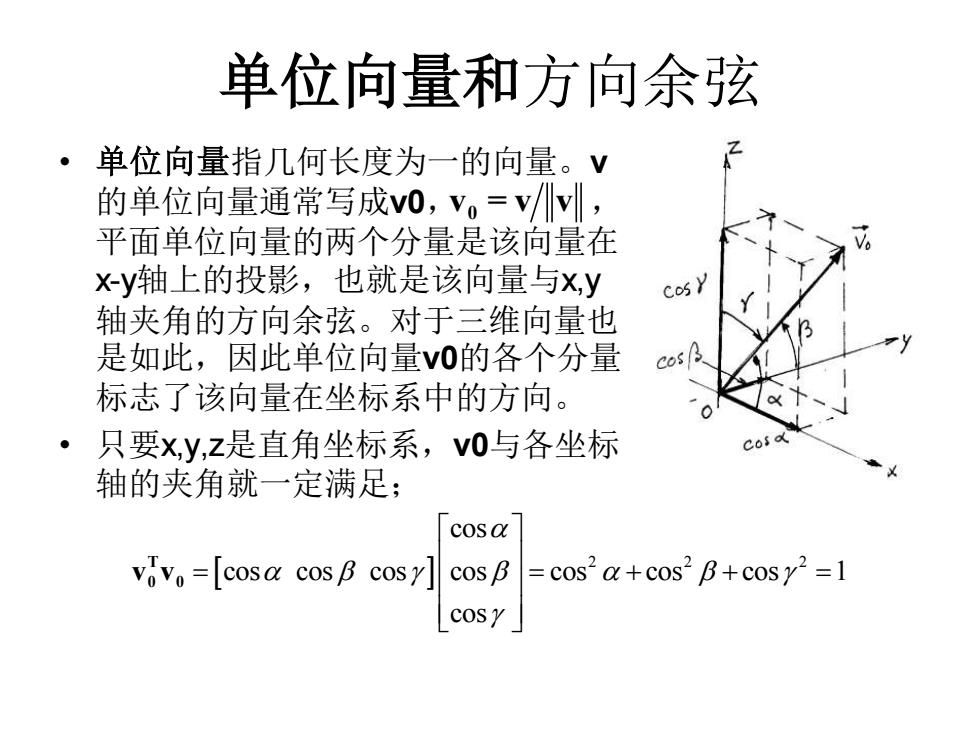
单位向量和方向余弦 • 单位向量指几何长度为一的向量。v 的单位向量通常写成v0, , 平面单位向量的两个分量是该向量在 x-y轴上的投影,也就是该向量与x,y 轴夹角的方向余弦。对于三维向量也 是如此,因此单位向量v0的各个分量 标志了该向量在坐标系中的方向。 • 只要x,y,z是直角坐标系,v0与各坐标 轴的夹角就一定满足; 0 v = v v 2 2 2 cos cos cos cos cos cos cos cos 1 cos = = + + = T 0 0 v v
数量积及其应用 两向量u和v的数量积也称为点乘(dot product)。其定义为 uv=ucosθ=vu (4.2.1) ·其中0为两个向量u和V之间的夹角。数量积的几何意义是 把u乘以v在u方向的投影,也是v乘以u在v方向的投影。 ·右图,用余弦定理得 lu-v2 =lu2+v12-2vlcose ·移项得到: u·vcos0=4M+22 啡 ·若用列矩阵表示向量u和V,则可写成 uv-=%+a4%- =u"v 对于空间向量,同样有:uV=4y+42y2+4y3=uv
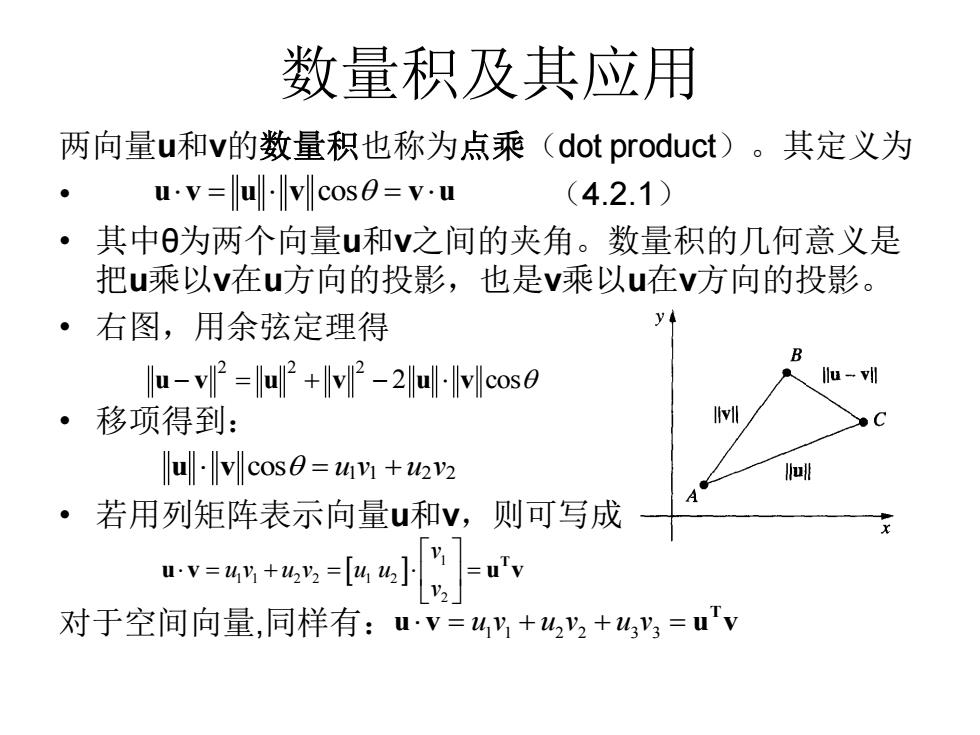
数量积及其应用 两向量u和v的数量积也称为点乘(dot product)。其定义为 • (4.2.1) • 其中θ为两个向量u和v之间的夹角。数量积的几何意义是 把u乘以v在u方向的投影,也是v乘以u在v方向的投影。 • 右图,用余弦定理得 • 移项得到: • 若用列矩阵表示向量u和v,则可写成 对于空间向量,同样有: u v u v v u = = cos 2 2 2 u v u v u v − = + − 2 cos u v = + cos u v u v 1 1 2 2 1 1 1 2 2 1 2 2 v u v u v u u v = + = = T u v u v 1 1 2 2 3 3 = + + = u v u v u v T u v u v

向量正交条件 两个有重要应用价值的结果: (1)两向量u,V之间的夹角: cos=uovo=uo'vo (2)两向量u,V相互正交的条件为: uv=<u,V>=0 例4.3设u=[4;2],V=[-1.5;3],求u和v的几何长度及它们的 单位向量,并求此两个向量与轴的夹角,画图说明。 解:u的几何长度为: u=V4+2=4.47 v的几何长度为:w=V1.5)'+32=3.39 v1.5,3) u4,2) 单位向量 4-3” 3/3.39 因 uv=uTv=0,知u,V正交
向量正交条件 两个有重要应用价值的结果: (1)两向量u, v之间的夹角: (2)两向量u, v相互正交的条件为: 例4.3 设u=[4;2],v=[-1.5;3],求u和v的几何长度及它们的 单位向量,并求此两个向量与x轴的夹角,画图说明。 解: u的几何长度为: v的几何长度为: 单位向量 因 ,知u,v正交。 0 0 0 0 cos = = T u v u v = = , 0 T u v u v 2 2 u = + = 4 2 4.47 ( ) 2 2 v = + = -1.5 3 3.39 -2 -1 0 1 2 3 4 -1 0 1 2 3 4 5 6 u(4,2) v(1.5,3) 0 4 / 4.47 1.5 / 3.39 , 2 / 4.47 3 / 3.39 − = = u v0 = = 0 T u v u v

解本题的MATLAB程序pla403 u=[4;2],V=[-1.5;3],x0=[1;0],%输入向量数据 u0=u/normu,v0=v/norm(W)%求u,v的单位向量 thetau=acos(u0*x0), %求u,V与x轴夹角 thetav=acos(vO'*x0) thetauv=acos(u0'*v0) %求u,V之间的夹角 plotangle(x,y) %绘制向量夹角 程序运行结果为: ·u=ac0s(u0T*x0)=0.4636【弧度】 ·v=acos(u0T*y0)=2.0344【弧度】
解本题的MATLAB程序pla403 u=[4;2],v=[-1.5;3],x0=[1;0], % 输入向量数据 u0=u/normu, v0=v/norm(v) % 求u,v的单位向量 thetau=acos(u0‘*x0), % 求u,v与x轴夹角 thetav=acos(v0’*x0) thetauv=acos(u0’*v0) % 求u,v之间的夹角 plotangle(x,y) % 绘制向量夹角 程序运行结果为: • θu=acos(u0T*x0)=0.4636【弧度】 • θv=acos(u0T*y0)=2.0344【弧度】