
它反映了总体均值 2.常用统计量 的信息 样本均值 x=12x 样本方差 -对 它反映子总体方差 样本标准差:5=尽-2对
2. 常用统计量 样本均值 样本方差 = = n i Xi n X 1 1 = − − = n i Xi X n S 1 2 2 ( ) 1 1 它反映了总体均值 的信息 它反映了总体方差 的信息 = − − = = n i Xi X n S S 1 2 2 ( ) 1 1 样本标准差:
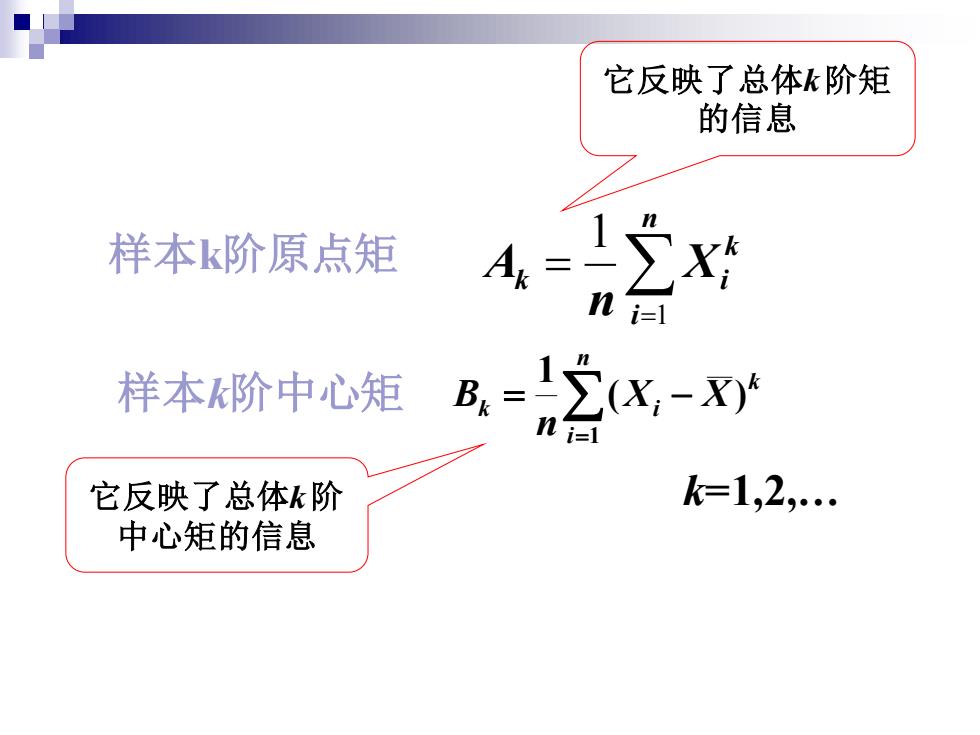
它反映了总体k阶矩 的信息 样本k阶原点矩 4-2x对 n i=I 样本阶中心矩 R=2x-X列 i1 它反映了总体k阶 k=1,2,. 中心矩的信息
样本k阶原点矩 样本k阶中心矩 = = n i k k Xi n A 1 1 = = − n i k k Xi X n B 1 ( ) 1 k=1,2,. 它反映了总体k 阶矩 的信息 它反映了总体k 阶 中心矩的信息

它们的观察值分别为: 样本均值 样本方差 a2 S= 样本标准差 a=4 ,k=1,2 样本k阶矩 ∑(x,-),k=1,2. 样本k阶中心矩
它们的观察值分别为: = = n i xi n x 1 1 [ ] 1 1 ( ) 1 1 1 2 2 1 2 2 = = − − − = − = n i i n i i x nx n x x n s = − − = n i xi x n s 1 2 ( ) 1 1 , 1,2 1 1 = = = x k n a n i k k i ( ) , 1,2 1 1 = − = = x x k n b n i k k i 样本均值 样本方差 样本标准差 样本k阶矩 样本k阶中心矩

说明 若总体X的阶矩E(X)记成存在, 则当n→0时,Ak”→4,k=1,2,. 证 X1,X2,X独立且与X同分布 X,X,X独立且与X*同分布 E(X)=E(X)=.E(X)=4 由辛钦定理AkP→4,k=1,2,. 依概率收敛的序列性质知道3为连续函数 g(A1A2,.3A)P→g(4,h,.,4x)
依概率收敛的序列性质知道 ( , , , ) ( , , , ) 1 2 1 2 k P g A A Ak ⎯→ g 则当 时, 若总体 的 阶矩 记成 存在, n → X k E X k k ( ) A ⎯→ ,k = 1,2, , k P k g为连续函数 证 X1 ,X2 , ,Xn独立且与X同分布k k n k k E(X1 ) = E(X2 ) =E(X ) = X1 k ,X2 k , ,Xn k独立且与X k同分布 由辛钦定理 A ⎯→ ,k = 1,2, , k P k 说明

3.经验分布函数 与总体分布函数F)相对应的统计量 设X1,X2,Xn是总体F的一个样本 用s(x),-0<x<+o表示X1,X2,Xn中不大于 x的随机变量的个数 定义经验分布函数为 F.(e)=1s(x,-0<x<+ 1
3. 经验分布函数 与总体分布函数F(x)相对应的统计量 设X1 ,X2 , ,Xn是总体F的一个样本 的随机变量的个数 用 表示 中不大于 x s x x X X Xn ( ), , , , − + 1 2 定义经验分布函数为 = s x − x + n Fn x ( ), 1 ( )