
第一节 二维随机变量 一、二维随机变量及其分布函数 二、二维离散型随机变量 三、二维连续型随机变量 四、两个常用的分布 五、小结
一、二维随机变量及其分布函数 二、二维离散型随机变量 三、二维连续型随机变量 四、两个常用的分布 五、小结 第一节 二维随机变量
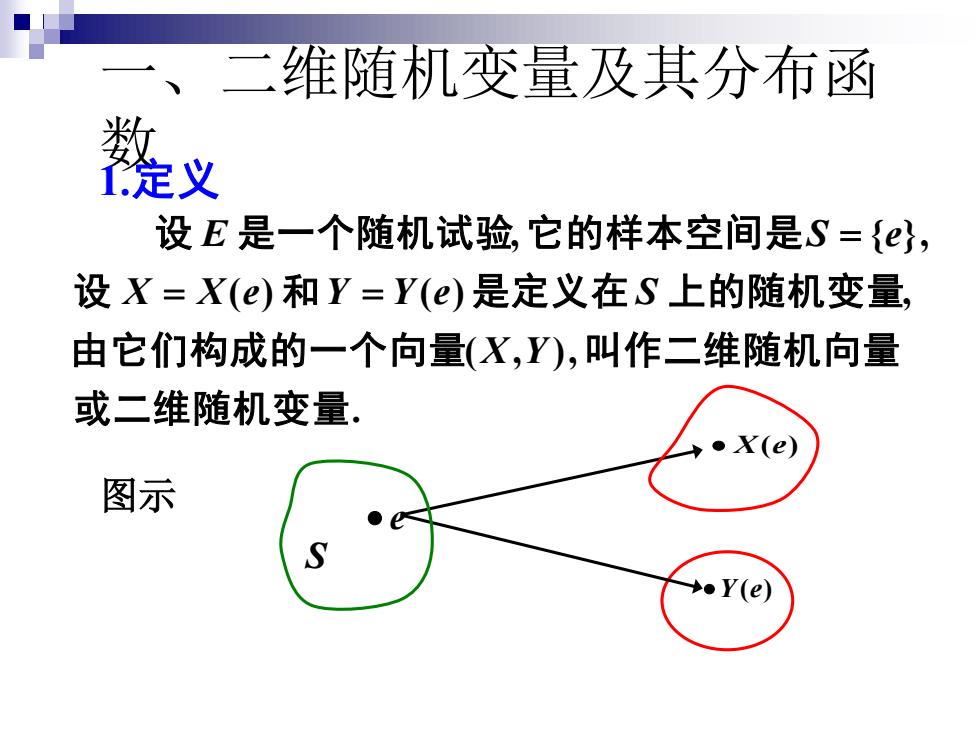
、二维随机变量及其分布函 数 义 设E是一个随机试验它的样本空间是S={}, 设X=X(e)和Y=Y(e)是定义在S上的随机变量, 由它们构成的一个向量(X,Y),叫作二维随机向量 或二维随机变量. ●x(e) 图示 ●Y(e)
图示 • e •Y(e) S • X(e) . ( , ), ( ) ( ) , , { }, 或二维随机变量 由它们构成的一个向量 叫作二维随机向量 设 和 是定义在 上的随机变量 设 是一个随机试验 它的样本空间是 X Y X X e Y Y e S E S e = = = 一、二维随机变量及其分布函 1. 数定义

实例1 炮弹的弹着点的 位置(X,Y)就是一个二维 随机变量. 实例2考查某一地区学前 儿童的发育情况,则儿童的 身高H和体重W就构成二 维随机变量(H,W). 说明 二维随机变量(X,Y)的性质不仅与X、Y 有关,而且还依赖于这两个随机变量的相互关系
实例1 炮弹的弹着点的 位置 ( X, Y ) 就是一个二维 随机变量. 二维随机变量 ( X, Y ) 的性质不仅与 X 、Y 有关,而且还依赖于这两个随机变量的相互关系. 实例2 考查某一地 区学前 儿童的发育情况 , 则儿童的 身高 H 和体重 W 就构成二 维随机变量 ( H, W ). 说明

2.二维随机变量的分布函数 ()分布函数的定义 设(X,Y)是二维随机变量对于任意实数x,y, 二元函数: F(x,y)=P{(X≤x)∩(Y≤y)}=P{X≤x,Y≤y} 称为二维随机变量(X,Y)的分布函数或称为随 机变量X和Y的联合分布函数
2.二维随机变量的分布函数 (1)分布函数的定义 . ( , ) , ( , ) {( ) ( )} { , } : ( , ) , , , 机变量 和 的联合分布函数 称为二维随机变量 的分布函数 或称为随 二元函数 设 是二维随机变量对于任意实数 X Y X Y F x y P X x Y y P X x Y y X Y x y = =

F(x,y)的函数值就是随机点落在如图所示区 域内的概率 (x,y) X≤x,Yy 文
o x y (x, y) • X x,Y y . ( , ) 域内的概率 F x y 的函数值就是随机点落在如图所示区