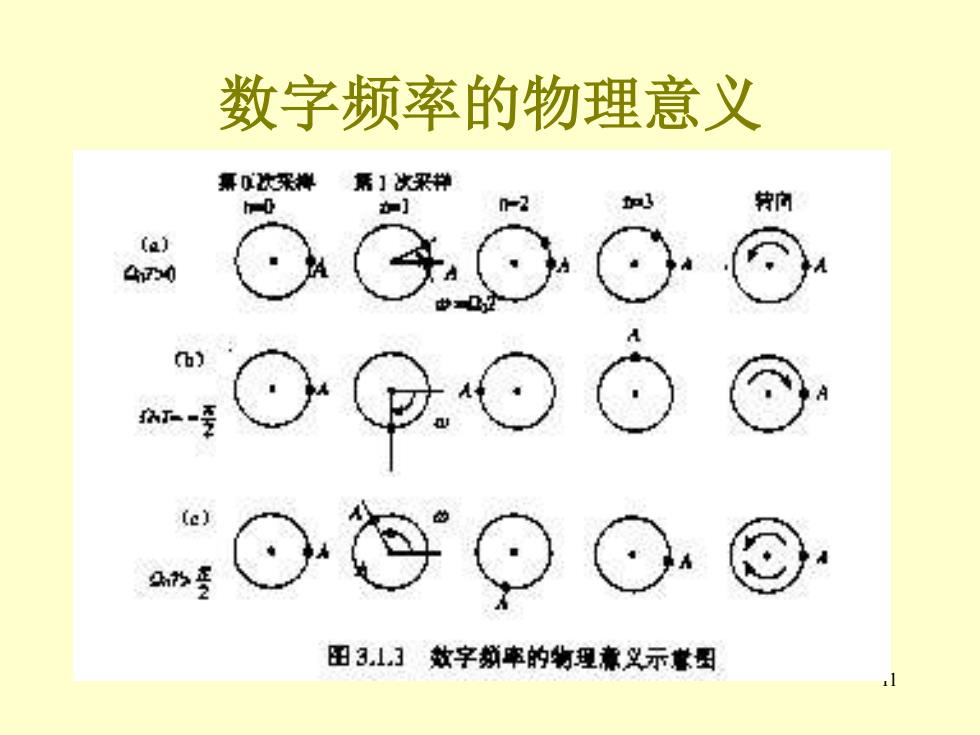
数字频率的物理意义 幂次采操屏】次采# 0 ] 转向 (a) 4h0 ( 田313效字州串的物理素义示营图
11 数字频率的物理意义

数字频率与模拟频率的关系 数字频率w=QT 00=0T 0-2Fs Fs 20 20+2F 模拟频率Q 2 图3.1.4模拟频率和数字频率的关系 。1 模拟频率和数字频率之间的映射关系如上图所 示。多个模拟频率映射到同一数字频率,这是 多点对一点的映射。 12
12 数字频率与模拟频率的关系 • 模拟频率和数字频率之间的映射关系如上图所 示。多个模拟频率映射到同一数字频率,这是 多点对一点的映射。 图 3.1.4 模拟频率和数字频率的关系

周期信号的频谱 非正余弦周期连续信号的频率分量用傅立 叶级数来表示,其傅立叶级数对可表为: ()ed k=0,士1,±2, x(t)=Xge oo =e 其中P为信号周期,2。=2P为信号的基 波频率,k为谐波的阶次,可以看出,连 续周期信号的频谱是离散的。前述纯正 余弦信号是其最简单的例子。 13
13 周期信号的频谱 非正余弦周期连续信号的频率分量用傅立 叶级数来表示,其傅立叶级数对可表为: 其中P为信号周期,Ω0=2π/P为信号的基 波频率,k为谐波的阶次,可以看出,连 续周期信号的频谱是离散的。前述纯正 余弦信号是其最简单的例子 。 − − = = 2 2 ( ) 0, 1, 2, 1 0 P p jk t k x t e dt k P X k j k k k jk t k x t X e X X e = = =− 0 ( )

连续信号的频谱 非周期连续信号的傅立叶变换对: x(j)=limXP=x(t)e-odt P00 0=,Xen 这种广义积分的成立是有条件的。它要求 x()满足绝对可积条件: (tdi<o 14
14 连续信号的频谱 非周期连续信号的傅立叶变换对: 这种广义积分的成立是有条件的。它要求 x(t)满足绝对可积条件: ( ) − − → X j = X P = x t e dt j t m P ( ) lim − x t = X j e d j t ( ) 2 1 ( ) − x(t) dt

连续信号的频谱 ·从统一的观点出发,周期连续信号只是它的特 例。谱是一种分布密度的概念,它的作用量应 该和它在频谱图上所围的面积成正比。傅立叶 级数可以看成在2=k2的频率点附近,集中了 幅度极大的频谱 。 ·傅立叶系数是对傅立叶变换(频谱)的采样, 而傅立叶变换则可看成对傅立叶系数的拟合插 补。因为一个是密度,另一个则是密度对频率 的积分,两者之间差一个频率(或时间)量纲。 15
15 连续信号的频谱 • 从统一的观点出发,周期连续信号只是它的特 例。谱是一种分布密度的概念,它的作用量应 该和它在频谱图上所围的面积成正比。傅立叶 级数可以看成在Ω=kΩ0的频率点附近,集中了 幅度极大的频谱 。 • 傅立叶系数是对傅立叶变换(频谱)的采样, 而傅立叶变换则可看成对傅立叶系数的拟合插 补。因为一个是密度,另一个则是密度对频率 的积分,两者之间差一个频率(或时间)量纲