Mathenatica 4-[Untitled-1 * 当H=0.1时振幅很 File Edit Cell Format Input Kernel Find Window Help 小,曲线是一个椭圆; 播Untitled-1* H=2对应于振幅为元 P1ot[1-Cos[x],{x,-1.5Pi,1.5Pi] 的情况,曲线仍闭合, Plot [[10.1-1+Cos[x],-10.1-1+cos[x],1-1+Cos[x],I -√1-1+C0s[x],V2-1+Cos[xJ,-√2-1+C0s[x灯, 但两端凸出略呈尖 √3.5-1+cos[x],-V3.5-1+C0s[x]},{x,-1.5P1,1.5P1)] 角状;H=3.5时曲线 分裂成上下两支,分 别对应于摆锤顺时 针和逆时针的旋转; H=2是介于往复摆 动与单向旋转之间 的临界状态,它在两 端交叉成尖角,此处 对应于摆锤在正上 方的不稳定位置这 条把两种运动形式 分开的曲线称为 “相分界线
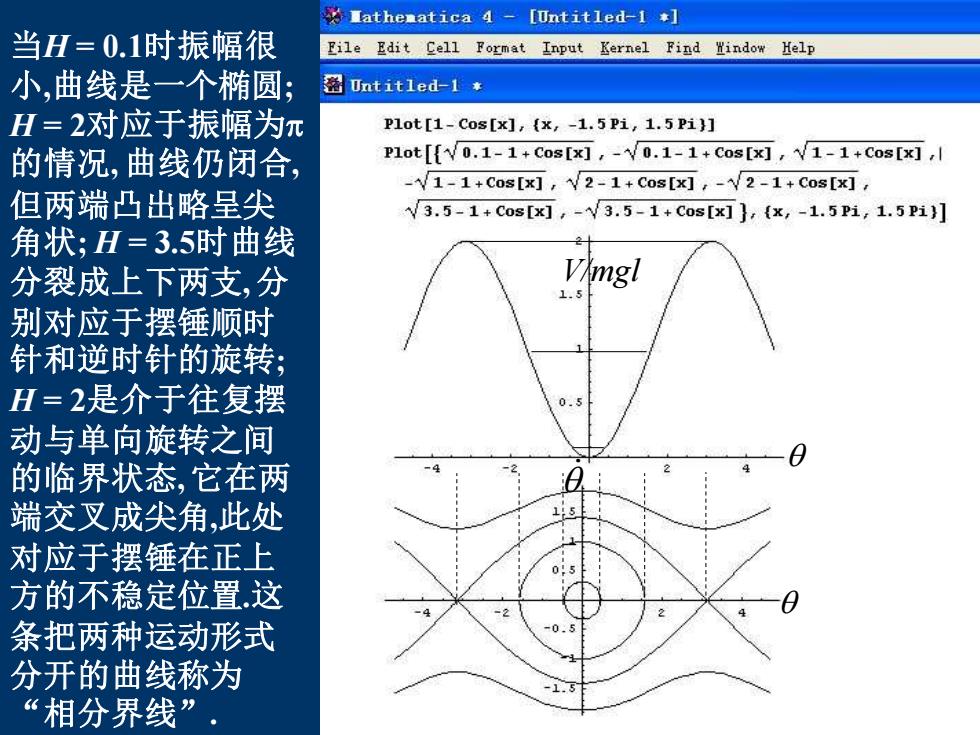
V/mgl 当H = 0.1时振幅很 小,曲线是一个椭圆; H = 2对应于振幅为 的情况, 曲线仍闭合 , 但两端凸出略呈尖 角状; H = 3.5时曲线 分裂成上下两支, 分 别对应于摆锤顺时 针和逆时针的旋转; H = 2是介于往复摆 动与单向旋转之间 的临界状态, 它在两 端交叉成尖角 ,此处 对应于摆锤在正上 方的不稳定位置 . 这 条把两种运动形式 分开的曲线称为 “相分界线”

(2)摆锤的速度=10,故动能为E=2ml202,从而 E=Er+V=ml202+mgl(1-Cos0)=C 或者H=E_l mgl 2g +1-cs9所以0-23-1+cos 分别把给定的H值带入,则由每个值就可以画出角速度与它的 关系(见上图 (3)线位移x=l,计算势能在平衡点的二阶导数: d2V(x) 1d2V(0 mg dx 12d02 A=0 周期为: T=2π 2π
(2) 摆锤的速度 v = l , 故动能为 2 2 2 1 E ml k = , 从而 (1 cos ) C 2 2 2 1 E = Ek +V = ml + mgl − = 1 cos 2 2 = + − g l mgl E H 或者 所以 ( 1 cos ) 2 = H − + l g 分别把给定的H值带入, 则由每个值就可以画出角速度与它的 关系.(见上图) (3) 线位移x=l, 计算势能在平衡点的二阶导数: l V mg x l V x V = = = = =0 2 2 2 0 2 2 d 1 d ( ) d d ( ) ''(0) g l V m T 2 ''(0) 周期为: = 2 =

例3、弹簧振子一质量为的质点连接一个轻质弹簧,弹 簧振子的弹性系数为k.(1)做Vx)-x曲线,说明图上哪个范 围是振子能够达到的;(2)对于E,2E,3E,试做速度与位移 曲线,并讨论其对应的运动情况;(③)求弹簧振子的周期, 解:(1)振子的势能为:个八/ m V(x)=号kx-x)2 曲线是一条抛物线.在x=xo=0处有极小值,即这里是稳定 平衡点.表示总能量E的水平线与势能曲线之间相差的高 度代表动能E,因为动能恒正,所以运动只能在势能曲线 低于水平线的范围内才能实现,虚线的位置为其振幅. (2)振子的总能量为E=E+V=m2+,x2=C 显然,无论能量(或者振幅)大小,轨迹总是椭圆
例3、弹簧振子一质量为m的质点连接一个轻质弹簧,弹 簧振子的弹性系数为k.(1)做V(x)-x曲线,说明图上哪个范 围是振子能够达到的; (2)对于E,2E,3E, 试做速度与位移 曲线, 并讨论其对应的运动情况; (3) 求弹簧振子的周期. x0 m x k 解: (1)振子的势能为: f m ( ) 2 2 0 1 V(x) = k x − x 曲线是一条抛物线. 在x=x0 = 0处有极小值,即这里是稳定 平衡点. 表示总能量E的水平线与势能曲线之间相差的高 度代表动能Ek . 因为动能恒正, 所以运动只能在势能曲线 低于水平线的范围内才能实现, 虚线的位置为其振幅. (2) 振子的总能量为 C 2 2 2 1 2 1 E = Ek +V = mv + kx = 显然, 无论能量(或者振幅)大小, 轨迹总是椭圆