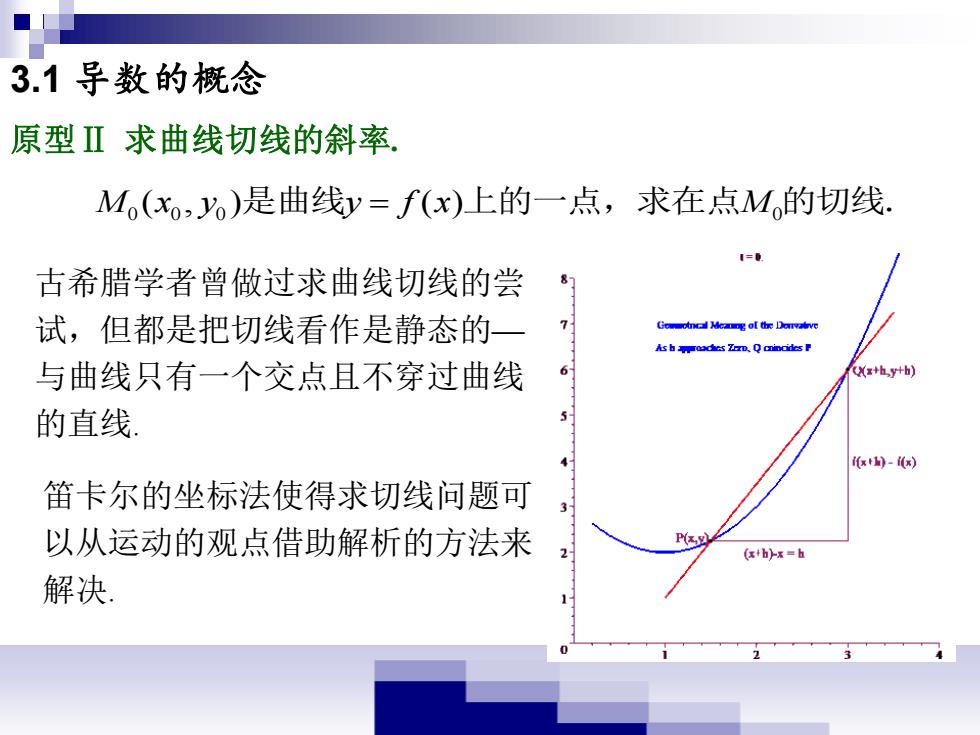
3.1导数的概念 原型Ⅱ求曲线切线的斜率 Mo(x,)是曲线y=f(x)上的一点,求在点M的切线. 1=0 古希腊学者曾做过求曲线切线的尝 试,但都是把切线看作是静态的 与曲线只有一个交点且不穿过曲线 Xx+hy+b) 的直线 x山-(x) 笛卡尔的坐标法使得求切线问题可 以从运动的观点借助解析的方法来 (x+h)x=h 解决
原型Ⅱ 求曲线切线的斜率. 0 0 0 0 M x y y f x M ( , ) ( ) 是曲线 = 上的一点,求在点 的切线. 古希腊学者曾做过求曲线切线的尝 试,但都是把切线看作是静态的— 与曲线只有一个交点且不穿过曲线 的直线. 3.1 导数的概念 笛卡尔的坐标法使得求切线问题可 以从运动的观点借助解析的方法来 解决
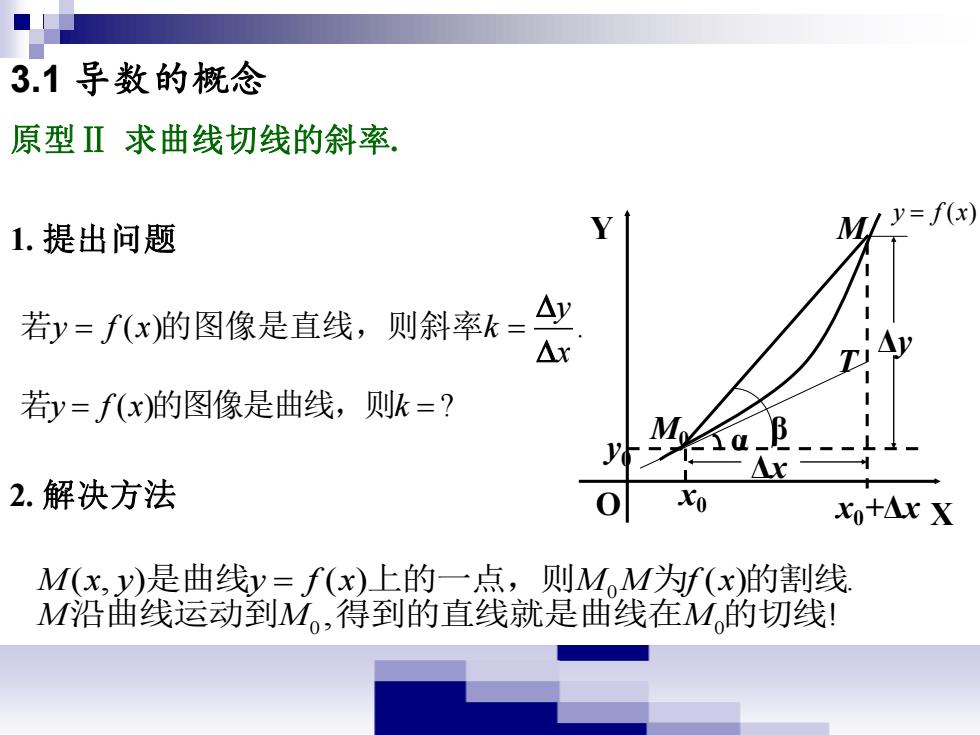
3.1导数的概念 原型Ⅱ求曲线切线的斜率 1.提出问题 Y M/ y=f(x) 若y=f(x)的图像是直线,则斜率k= △y △x 若y=f(x)的图像是曲线,则k=? 2.解决方法 x+△xX M(x,y)是曲线y=f(x)上的一点,则MM为f(x)的割线 M沿曲线运动到M,得到的直线就是曲线在M的切线划
1. 提出问题 ( ) . 若 的图像是直线,则斜率 y y f x k x = = 若y f x k = = ( ) ? 的图像是曲线,则 O X Y Δx M0 M Δy y0 x0 x0+Δx T α y = f (x) β 原型Ⅱ 求曲线切线的斜率. 3.1 导数的概念 2. 解决方法 0 0 0 ( , ) ( ) ( ) . , ! 是曲线 上的一点,则 为 的割线 沿曲线运动到 得到的直线就是曲线在 的切线 M x y y f x M M f x M M M =