在式(2.19)中,如果把初始电压U(0)也视为一个输入作用, 则根据线性系统的叠加原理,可以分别研究在输入电压U() 和初始电压U(O)作用时,电路的输出响应。若U(O)=0,则 有: U.(s)= U,(s) (2.20) RCs+1 当输入电压u,()一定时,电路输出响应的拉氏变换U(s)完全由 1/(RCs+1)所确定,式(2.20)亦可写为: U.(s) (2.21) U(s) RCs+1 当初始电压为零时,电路输出函数的拉氏变换U(S)与输入 函数拉氏变换U(S)之比,是一个只与电路结构及参数有关的函数
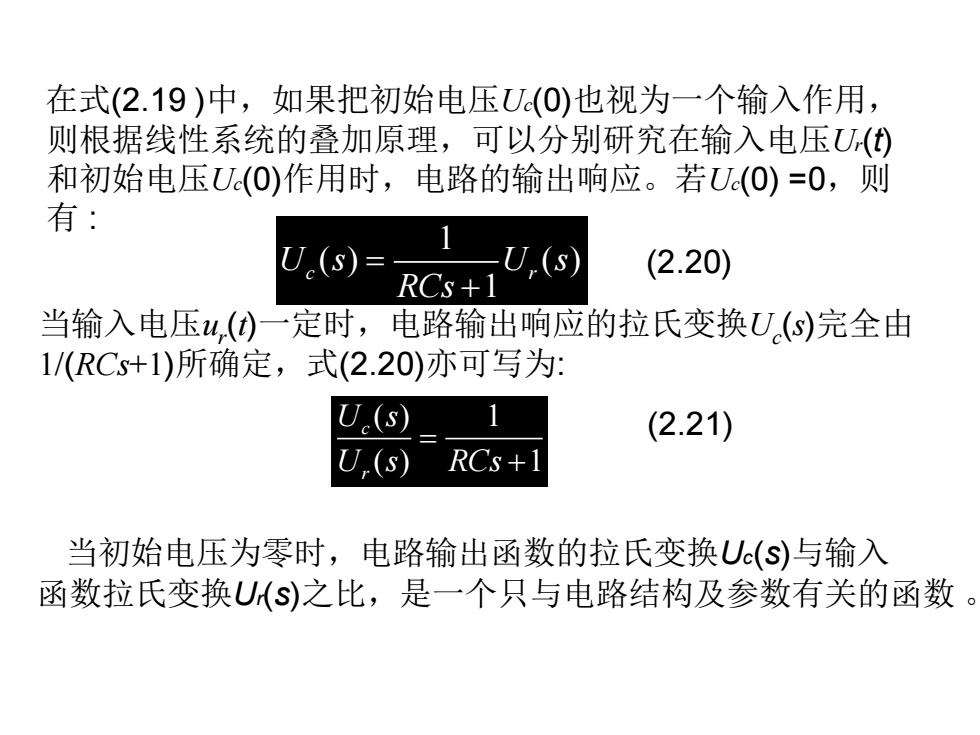
在式(2.19 )中,如果把初始电压Uc(0)也视为一个输入作用, 则根据线性系统的叠加原理,可以分别研究在输入电压Ur(t) 和初始电压Uc(0)作用时,电路的输出响应。若Uc(0) =0,则 有 : 1 ( ) ( ) 1 U s U s c r RCs = + (2.20) 当输入电压ur (t)一定时,电路输出响应的拉氏变换Uc (s)完全由 1/(RCs+1)所确定,式(2.20)亦可写为: ( ) 1 ( ) 1 c r U s U s RCs = + (2.21) 当初始电压为零时,电路输出函数的拉氏变换Uc(s)与输入 函数拉氏变换Ur(s)之比,是一个只与电路结构及参数有关的函数
式(2.21)来表征电路本身特性,称做传递函数,记为: G(s)= Ts +i U,(s) Ue(s) Ks) 式中T=RC。显然,传递函 数G(s)确立了电路输入电压 与输出电压之间的关系。 图2-6传递函数 传递函数可用图2-6表示。该图表明了电路中电压的传递 关系,即输入电压U(S),经过G(S)的传递,得到输出电压 U(S)=G(S)U(S)。 线性(或线性化)定常系统在零初始条件下,输出量的拉氏 变换与输入量的拉氏变换之比称为传递函数
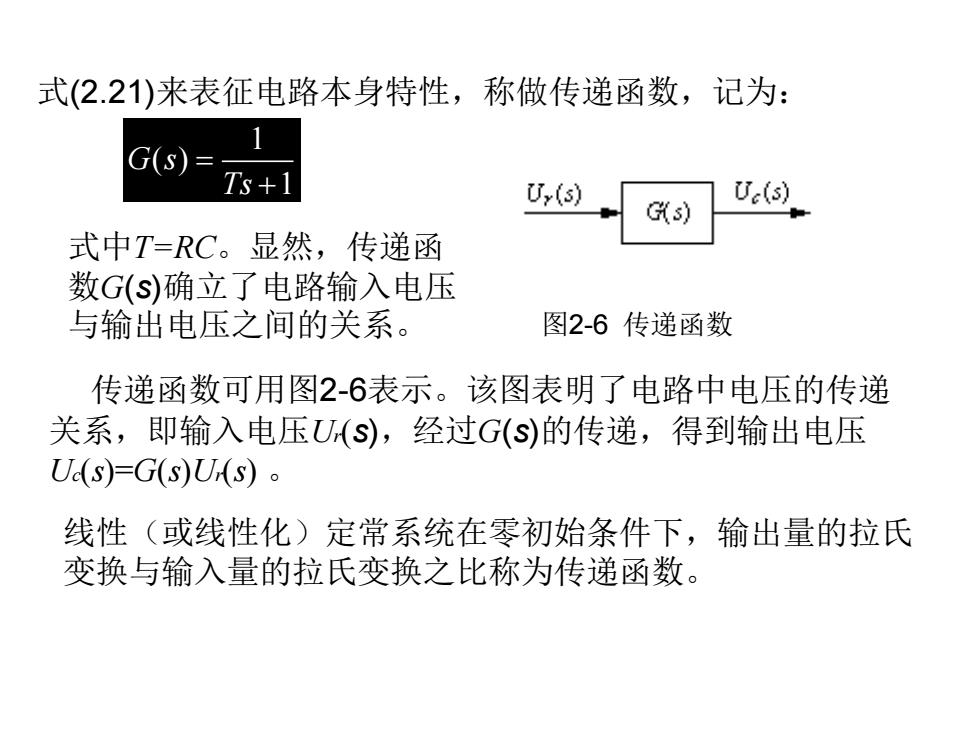
式(2.21)来表征电路本身特性,称做传递函数,记为: 1 ( ) 1 G s Ts = + 式中T=RC。显然,传递函 数G(s)确立了电路输入电压 与输出电压之间的关系。 图2-6 传递函数 传递函数可用图2-6表示。该图表明了电路中电压的传递 关系,即输入电压Ur(s),经过G(s)的传递,得到输出电压 Uc(s)=G(s)Ur(s) 。 线性(或线性化)定常系统在零初始条件下,输出量的拉氏 变换与输入量的拉氏变换之比称为传递函数