南阳师范学院：《数学分析》课程教学资源（课件讲稿）第八章 不定积分

四、基本积分表 由基本求导公式可得以下基本积分公式： 1.[0dx=C. 2.∫ldc=∫dx=x+C a+1 3.fx"dx=x +C(a≠-1，x>0) a+1 4.∫dr=Imx+c. 5.∫edr=e*+c 6Je'deaC

由基本求导公式可得以下基本积分公式: 1. 0d . x C  2. 1d d . x x x C      1 3. d ( 1, 0). 1 x x x C x             1 4. d ln | | . x x C x    5. e d e . x x x C    四、基本积分表 6. d . ln x x a a x C a   

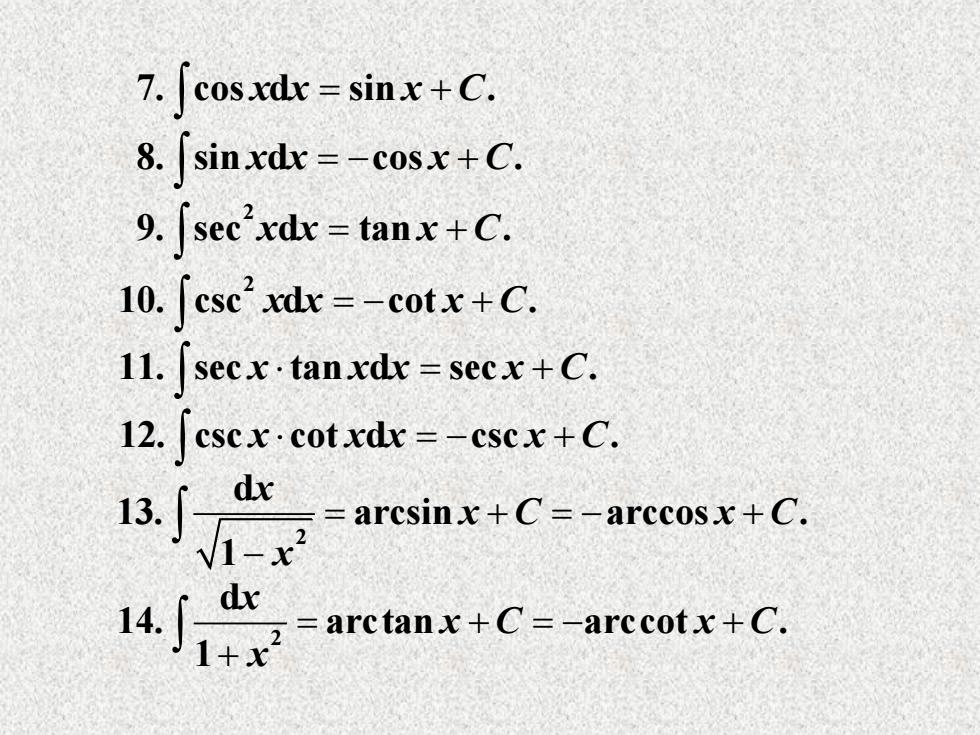
7.∫cosxd=sinx+C 8.sinxdx =-cosx+C. 9.sec'xdx =tanx+C. 10.「csc2xdr=-cotx+C 11.secx.tanxdx secx+C. 12.cscx.cotxdx=-cscx+C. 13. dx arcsinx+C=-arccosx+C. V-x 4 =arctanx+C=-arccotx+C

7. cos d sin . x x x C    8. sin d cos . x x x C     2 9. sec d tan . x x x C    2 10. csc d cot . x x x C     11. sec tan d sec . x x x x C     12. csc cot d csc . x x x x C      2 d 13. arcsin arccos . 1 x x C x C x        2 d 14. arctan arccot . 1 x x C x C x       

由导数线性运算法则可得到不定积分的线性运算 法则 定理8.3（不定积分的线性运算法则） 若函数f与g在区间I上都存在原函数k1,k2为 任意常数，则k∫+k2g在I上也存在原函数，且 ∫(kfx)+kgx)de=k∫fc)dr+k,Jgc)de. 例1p(x)=ax”+a1x"+…+n-1x+,则 jpw-名“t2r +x++ 4ax+ax+C. 2

由导数线性运算法则可得到不定积分的线性运算 定理 8.3 (不定积分的线性运算法则) 1 2 1 2 ( ( ) ( ) )d ( )d ( )d . k f x k g x x k f x x k g x x       上都存在原函数, k1 , k 若函数 与 在区间 f g I 2为 k f k g I 1 2 任意常数  在 上也存在原函数 且, , 则           n n n n a a a p x x x x x a x C n n 1 2 0 1 1 ( )d . 1 2 例1 ( ) , 1 1 0 1 n n n n p x  a x  a x   a  x  a   则 法则

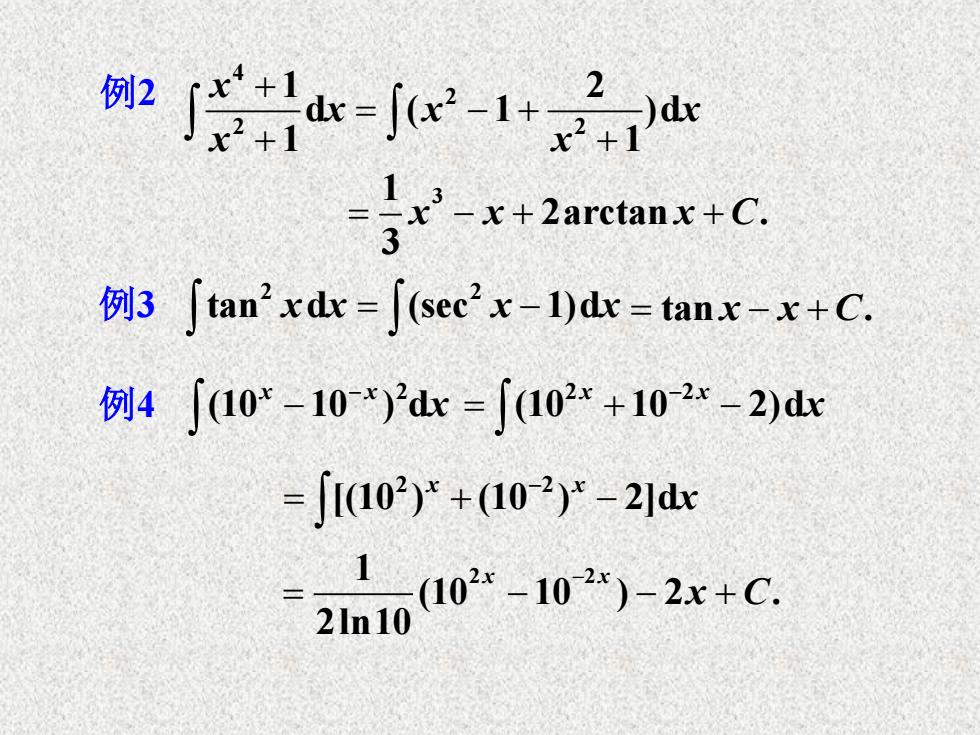
3水e2-1+ 1 x-x+2arctanx+C. 3 例3∫tan2xdr=∫sec2x-)dc=tanx-x+C 例4∫10*-10*)2dx=∫102-+102r-2)d =JI(102)+(102)*-21d xC

例 2         x x x x x x 4 2 2 2 1 2 d ( 1 )d 1 1     x x x C 1 3 2arctan . 3 例 3  x x 2 tan d    x x    tan . x x C 2 (sec 1)d      x x x 2 2 [(10 ) (10 ) 2]d 1 2 2 (10 10 ) 2 . 2ln10 x x x C      例 4    x x x 2 (10 10 ) d      x x x 2 2 (10 10 2)d

8.2导数的概念 ·一、换元积分法 ·二、分部积分法

• 一、换元积分法 • 二、分部积分法