南阳师范学院：《数学分析》课程教学资源（课件讲稿）第八章 不定积分

一、第一换元积分法 定理8.4（第一换元积分法） 设g(w)在[a,β]上有定义，且∫g(o)du=G(w+C. 又u=p(x)在a,b上可导，且a≤p(x)≤B,x∈[a,bl 则∫g(p(x)p'(x)dx-∫g(u)du =G()+C=G(p(x)+C.(1) 正因为dG(o(x)=G(e(x)p'w)=gg(yp'x dx 所以)式成立

定理8.4 (第一换元积分法) 设 在 上有定义， g u( ) [ , ]      且 g u u G u C ( )d ( ) . 又u  (x)在[a,b]上可导，且  (x)   , x[a,b]. 则     g x x x g u u ( ( )) ( )d ( )d    G(u)  C  G x C ( ( )) . (1)  证    d ( ( )) ( ( )) ( ) d G x G x x x 因为     g((x))(x). 一、第一换元积分法 所以(1)式成立

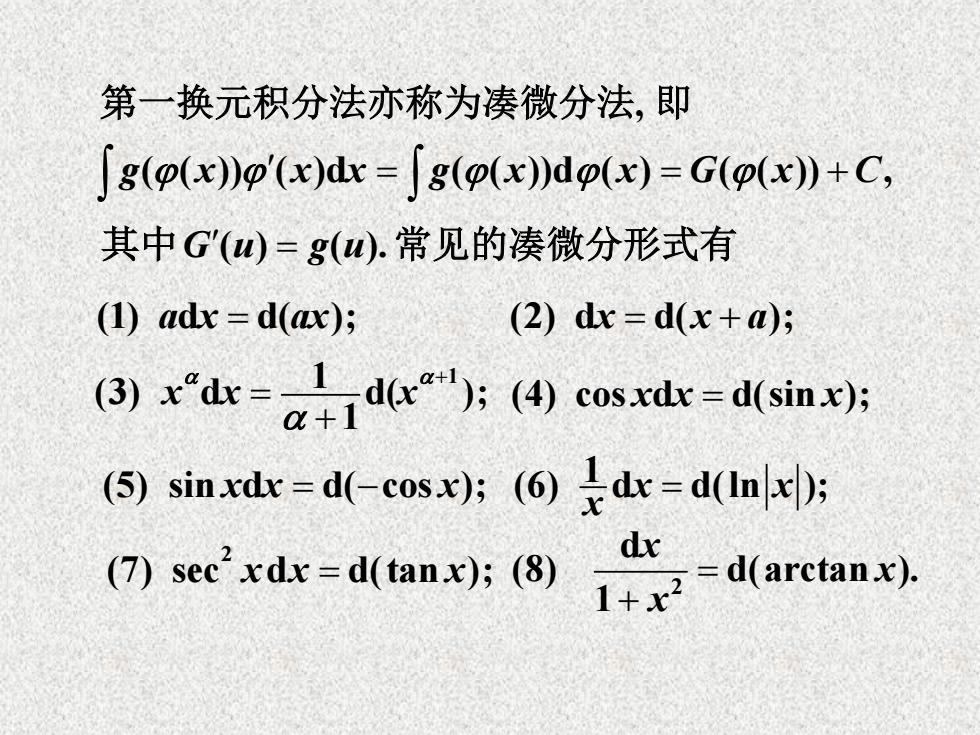
第一换元积分法亦称为凑微分法，即 ∫g(p(x)p'(x)dc=∫g(p(x)dp(x)=G(p(x)+C, 其中G'(四）=g(u).常见的凑微分形式有 (1)adx=d(ax); (2)dx=d(x+a); d)rdr=中dr5④cosa--d(sin: (⑤)sinxdx=d(-cosx;(⑥)dr=dlnx)月 dx (7)secxd-d(tan);(8)d(arctanx)

第一换元积分法亦称为凑微分法, 即       g x x x g x x G x C ( ( )) ( )d ( ( ))d ( ) ( ( )) ,      (1) d d( ); a x ax  (2) d d( ); x x a   1 1 (3) d d( ); 1 x x x       (4) cos d d(sin ); x x x  (5) sin d d( cos ); x x x   1 (6) d d(ln ); x x x  2 (7) sec d d(tan ); x x x  2 d (8) d(arctan ). 1 x x x   其中G u g u ( ) ( ).  常见的凑微分形式有

(a>0). 解 1+ =-arctanu+C

例 1 ( 0). d 2 2    a a xx 求 解         2 2 2 1d d 1 axax a x a x 2 1 d1 u a u    u C a  arctan  1 arctan . 1 C ax a  

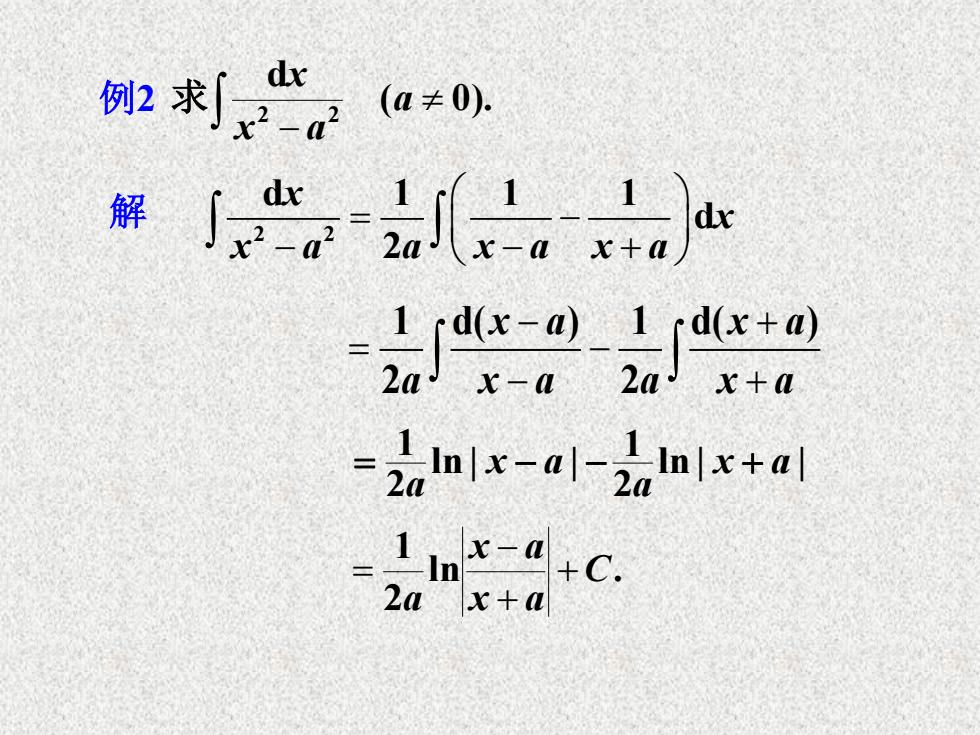
2灯“， (a≠0). 解∫a。d -2alx-al-2alnlx+al 2a Llnx-a 2ax+a +C

例 2 ( 0). d2 2    a x ax 求 解              2 2 d 1 1 1 d 2 x x x a a x a x a 1 d( ) 1 d( ) 2 2 x a x a a x a a x a        ln | | 21 ln | | 21 x a a x a a     ln . 21 C x a x a a   

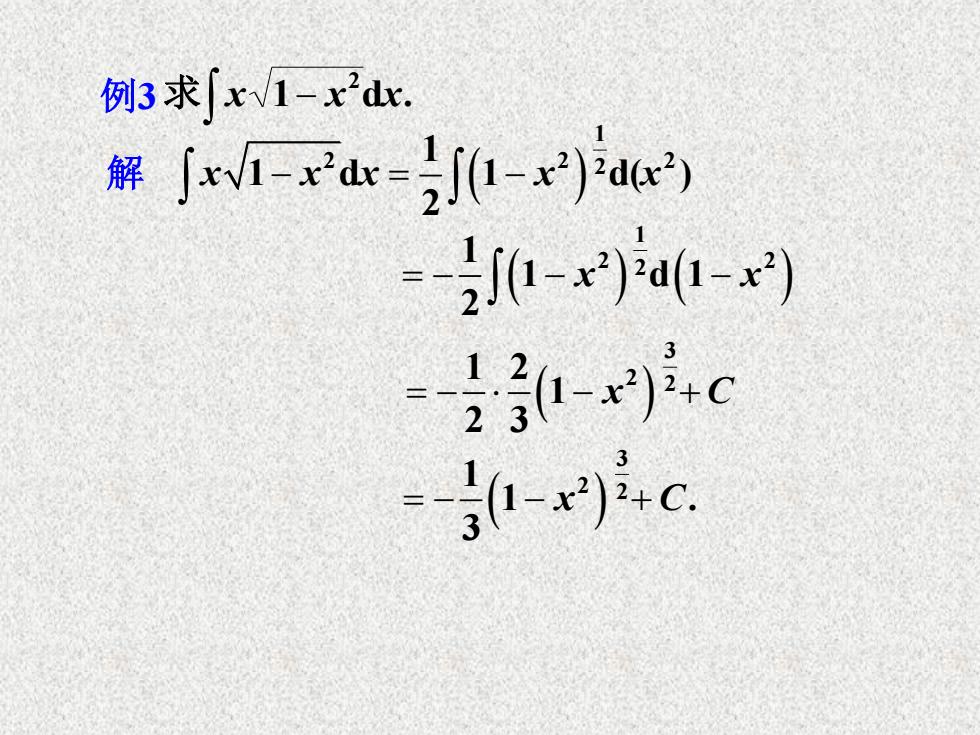
例3求∫xV1-x2dr. 解J小irdw-0-rae) =20-)a-） --)+c =-x)4c

例 3 1 d . 2 x x x  求  解   1 2 2 2 2 1 1 d 1 d( ) 2 x x x x x          1 2 2 2 1 1 d 1 2     x x    3 2 2 1 2 1 2 3      x C   3 2 2 1 1 . 3     x C