
定理8.1(原函数存在性定理) 若函数f在区间I上连续,则f在I上存在原函 数F,即F'(x)=f(x) 定理82(原函数族的结构性定理) 设F(x)是f(x)在区间I上的一个原函数,则 ()F(x)+C也是f()在I上的原函数,其中C ()fx)在I上的任意两个原函数之间,只可能相差 为任意常数 一个常数
定理8.2 (原函数族的结构性定理) 设 是 在区间 上的一个原函数 则 F x f x I ( ) ( ) , (i) ( ) ( ) , F x C f x I C 也是 在 上的原函数 其中 (ii) f (x) 在 I 上的任意两个原函数之间, 只可能相差 为任意常数. 一个常数. 定理8.1 (原函数存在性定理) 若函数 在区间 上连续 则 在 上存在原函 f I f I , 数 F, 即 F x f x ( ) ( ).

二、不定积分 定义2函数f在区间I上的全体原函数称为f 在【上的不定积分,记作 ∫fx)dr, 其中称x为积分变量,f(x)为被积函数, f(x)dx为积分表达式,「为积分号. 若F(x)是f(x)的一个原函数,则由定理8.2, f(x)dx=(F(x)+C CER)
f x x ( )d , 二、不定积分 定义2 函数 在区间 上的全体原函数称为 f I f 在 I 上的不定积分, 记作 其中称 x f x 为积分变量, ( ) , 为被积函数 f x x ( )d . 为积分表达式 , 为积分号 若 是 的一个原函数 则由定理 F x f x ( ) ( ) , 8.2, f x x F x C C ( ) d ( ) R .

为方便起见,我们记「f(x)dx=F(x)+C.其中 C为任意常数. 由此,从例1())(iv)可得: j小agr+C axn6 小-x-ki-+arcsin)+小c
为方便起见, 我们记 f x x F x C ( )d ( ) . 其中 由此, 从例 1(ii) (iii) (iv)可得: x x x C 2 3 1 d , 3 2 2 d ln( 1 ) , 1 x x x C x 2 2 1 1 d 1 arcsin . 2 x x x x x C C 为任意常数
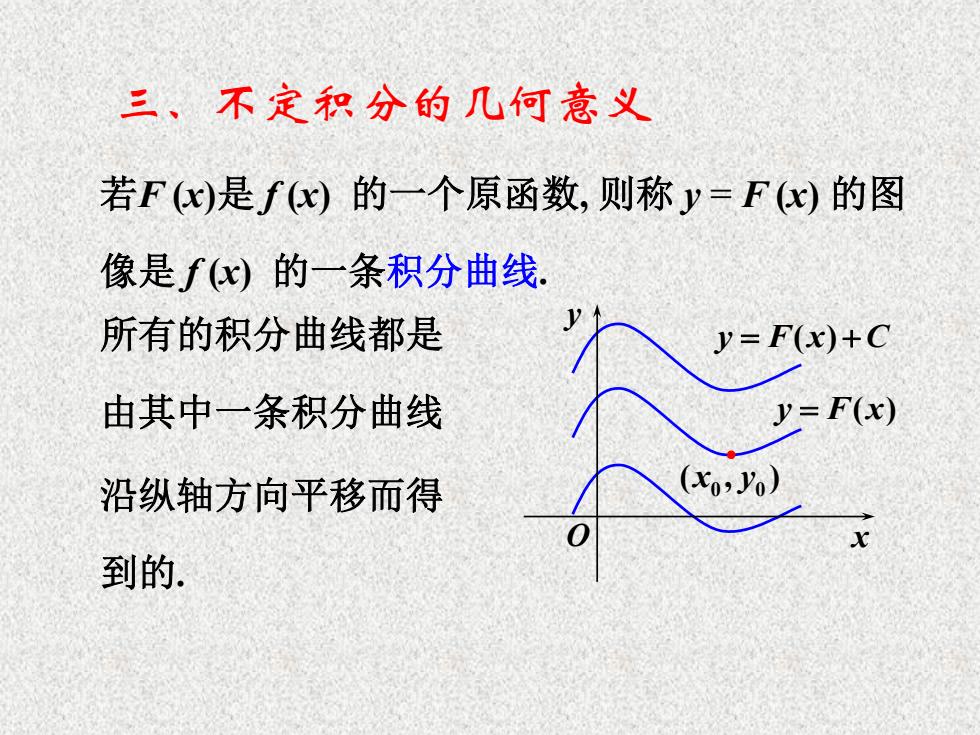
三、不定积分的几心何意义 若F(x)是fx)的一个原函数,则称y=Fx)的图 像是f(x)的一条积分曲线: 所有的积分曲线都是 y=F(x)+C 由其中一条积分曲线 y=F(x) 沿纵轴方向平移而得 (x0,Jy0) 到的
若F (x)是 f (x) 的一个原函数, 则称 y = F (x) 的图 所有的积分曲线都是 三、不定积分的几何意义 y F x C ( ) 0 0 ( , ) x y y F x ( ) O x y 像是 f (x) 的一条积分曲线. 到的. 沿纵轴方向平移而得 由其中一条积分曲线

满足条件F(x)=y,的原函数正是在积分曲线中 通过点(x,y)的那一条积分曲线. 例如,质点以匀速运动时,其路程函数 st)=∫dt=y,t+C: 若t时刻质点在so处,且速度为v,则有 s(t)=vo(t-to)+5o
例如, 质点以匀速 v0 运动时, 其路程函数 0 0 s t v t v t C ( ) d . 若 t0 时刻质点在 s0 处, 且速度为 v0 , 则有 0 0 0 ( ) ( ) . s t v t t s 满足条件 F x y ( )0 0 的原函数正是在积分曲线中 ( , ) 0 0 通过点 x y 的那一条积分曲线