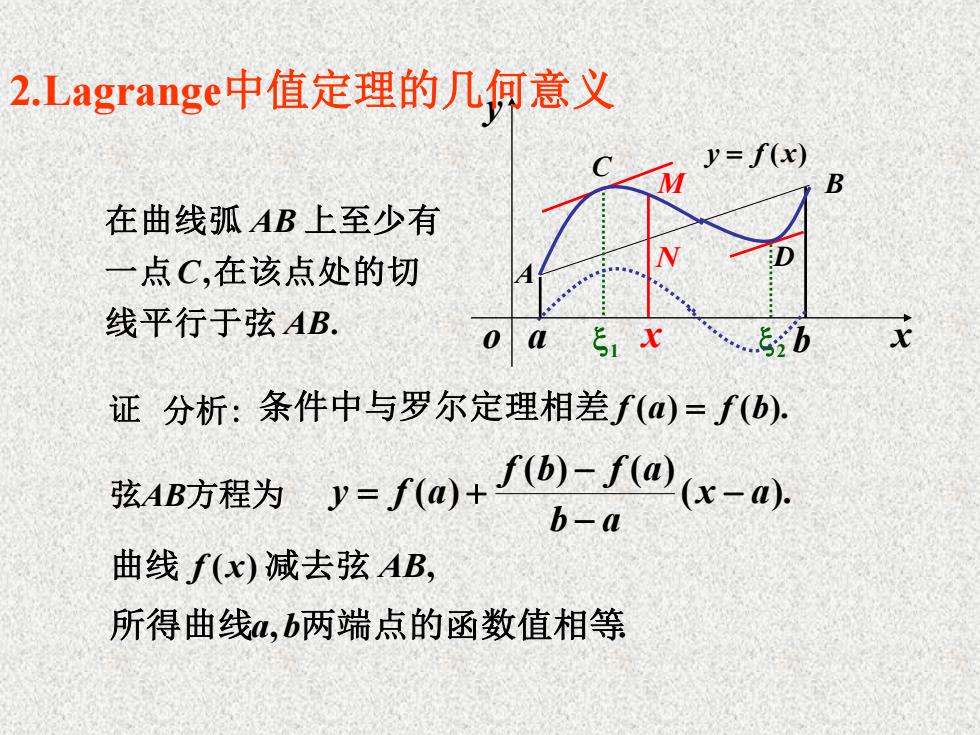
2.Lagrange中值定理的几何意义 y=f(x) 在曲线弧AB上至少有 一点C,在该点处的切 线平行于弦AB. .5b 证分析:条件中与罗尔定理相差f(a)=f(b). 弦4B防程为y=fo+fb-f@(x-a b-a 曲线f(x)减去弦AB, 所得曲线α,b两端点的函数值相等
o a 1 x 2 b x y y = f (x) A B C N D M . , AB C AB 线平行于弦 一点 在该点处的切 在曲线弧 上至少有 证 分析: 条件中与罗尔定理相差 f (a) = f (b). 弦AB方程为 ( ). ( ) ( ) ( ) x a b a f b f a y f a = 曲线 f (x) 减去弦 AB, 所得曲线a,b两端点的函数值相等. 2.Lagrange中值定理的几何意义

作辅助函数 F(x)-S(x)-If(@)+J(b)-f(@(x-a)l. b-a F(x)满足罗尔定理的条件 则在(a,b)内至少存在一点起,使得F'(飞)=0. 即f'传)-f6)-fa-=0 b-a 或f(b)-f(@)=f'(传)b-): 注意:拉氏公式精确地表达了函数在一个区间上的增量与函 数在这区间内某点处的导数之间的关系
作辅助函数 ( )]. ( ) ( ) ( ) ( ) [ ( ) x a b a f b f a F x f x f a = F(x)满足罗尔定理的条件, 则在(a,b)内至少存在一点,使得 F() = 0. 0 ( ) ( ) ( ) = b a f b f a 即 f 或 f (b) f (a) = f ()(b a). 注意:拉氏公式精确地表达了函数在一个区间上的增量与函 数在这区间内某点处的导数之间的关系

设f(x)在a,b]上连续,在(a,b)内可导 x。,x。+△x∈(a,b),则有 f(x。+△x)-f(x)=f'(x+0△x)·△x(0<0<1) 也可写成△y=f'(,+0△x)△x(0<0<1), 拉格朗日中值公式又称有限增量公式: 拉格朗日中值定理又称有限增量定理
设 f (x)在[a,b]上连续,在(a,b)内可导, ( ) ( ) ( ) (0 1). f x0 x f x0 = f x0 x x x0 , x0 x (a,b), 则有 ( ) (0 1). 也可写成y = f x0 x x 拉格朗日中值定理又称有限增量定理. 拉格朗日中值公式又称有限增量公式

3.Lagrange公式的几种形式 1)fb)-f(a)=f'(5)b-0)(在与b之间 2-a (在a与b之间 3)f(b)-f(ad)=f'Ia+0(b-1b-@)(0<0<1) 4)f(x+△x)-f(x)=f'(x+x)△x(0<B<I)
1) f (b) f (a) = f ( )(b a) b a f b f a f = ( ) ( ) 2) ( ) (在a与b之间) (在a与b之间) 3) f (b) f (a) = f [a (b a)](b a) (0 1) 4) f (x x) f (x) = f (x x)x (0 1) 3.Lagrange公式的几种形式

4.Lagrange中值定理的应用 (1)导数相等的函数之间的关系 推论1设f(x)在(a,b)可微且f'(x)≡0,则f(x)在 (a,b)上恒为常数。 推论1'设f(x),8(x)在(a,b)可微且f'(x)=g'(x),则 彐常数C使 f(x)=g(x)+C
4.Lagrange中值定理的应用 (1)导数相等的函数之间的关系 上恒为常数。 设 在 可微且 ,则 在 ( , ) ( ) ( , ) ( ) 0 ( ) a b 推论1 f x a b f x f x 常数 使 设 在 可微且 ,则 C f x g x a b f x g x 推论 1 ( ), ( ) ( , ) ( ) = ( ) f (x) = g(x) C