
(2)证明恒等式 例4证明arcsinx+arccos=7,(-1≤x≤). 证设f(x)=arcsinx+arccos x,x∈-l, w=en .f(x)=C,x∈[-1,1川 f(0)=arcsin0+arccos0=0+ 元元 2 2 即C= 元 2 .arcsin x+arccosx= 2
(2)证明恒等式 例 4 ( 1 1). 2 证明arcsin x arccos x = , x 证 设 f (x) = arcsin x arccos x, x[1,1] ) 1 1 ( 1 1 ( ) 2 2 x x f x = = 0. f (x) C, x [1,1] 又 f (0) = arcsin0 arccos 0 2 0 = , 2 = . 2 即C = . 2 arcsin arccos x x =

(3)证明不等式 证明当>0丽1+1+K 例5 证 设f(x)=n(1+x), f(x)在0,x上满足拉氏定理的条件, .fx)-f0)=f'"(传x-0,(0<5<x) j0)=0,f)=1+ 由上式得11+)=1+ξ 又:0<<x一1<1+5<1+x一1+x1+ 1 11, <X, 1+x1+ 即,x<ln(1+x)<x. 1+x
例5 ln(1 ) . 1 0 , x x x x x 证明当 时 证 设 f (x) = ln(1 x), f (x)在[0, x]上满足拉氏定理的条件, f (x) f (0) = f ()(x 0), (0 x) , 1 1 (0) 0, ( ) x f f x = = 由上式得 , 1 ln(1 ) = x x 又0 x 1 1 1 x 1, 1 1 1 1 x , 1 1 x x x x ln(1 ) . 1 x x x x 即 (3)证明不等式

(4)判定函数的单调性 推论2设函数y=f(x)在[a,b]上连续,在(a,b) 内可导,则 (1)如果在(a,b)内f'(x)≥0,那未函数y=f(x)在 [a,b]上单调增加; (2)如果在(a,b)内f'(x)≤0,那末函数y=f(x) 在[a,b]上单调减少
[ , ] . (2) ( , ) ( ) 0 ( ) 在 上单调减少 如果在 内 ,那末函数 a b a b f x y = f x 上单调增加; ()如果在 内 ,那末函数 在 [ , ] 1 ( , ) ( ) 0 ( ) a b a b f x y = f x (4)判定函数的单调性 推论 2 内可导,则 设函数y = f (x)在[a,b]上连续,在(a,b)
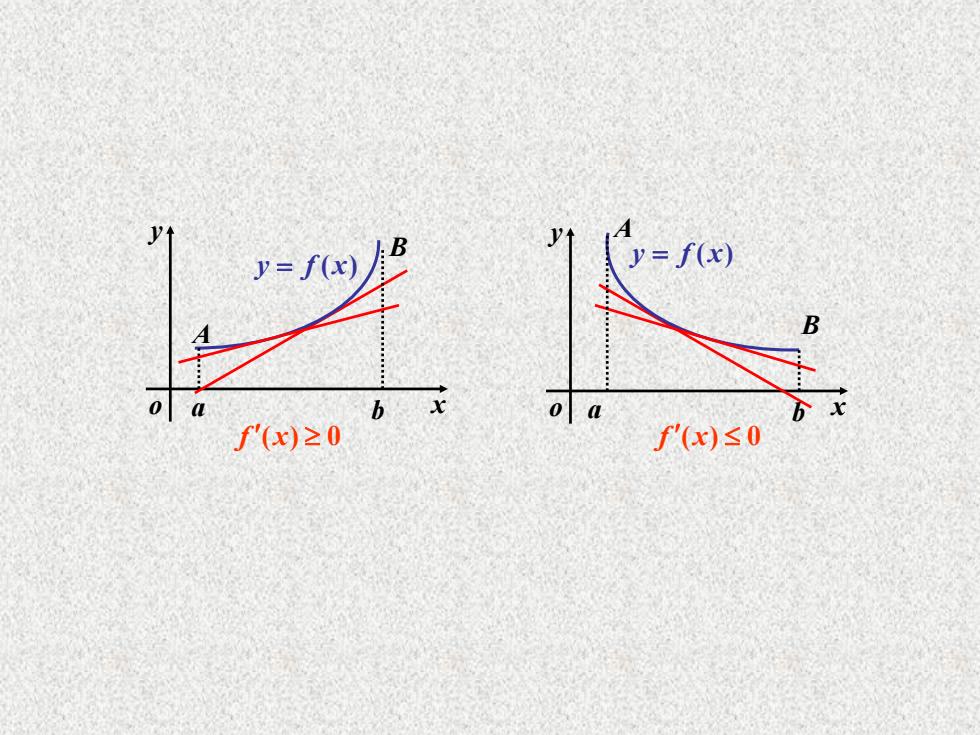
y=f(x) B 1=四 B 0 o a f'(x)≥0 f'(x)≤0
x y o y = f (x) x y o y = f (x) a b A B f (x) 0 f (x) 0 a b B A

证x1,x2∈(,b),且x1<x2,应用拉氏定理,得 f(x2)-fx)=f'(5)x2-x) (x<5<x2) .x2-x1>0) 若在(a,b)内,f'(x)≥0, 则f'()≥0 f(x2)≥f(x).∴.y=f(x)在a,b上单调增加 若在(a,b)内,f'(x)≤0,则f'(5)≤0, ·f(x2)≤f(x).y=f(x)在a,b上单调减少
证 , ( , ), x1 x2 a b , 且 x1 x2 应用拉氏定理,得 ( ) ( ) ( )( ) ( ) 2 1 x2 x1 x1 x2 f x f x = f 0, x2 x1 若在(a,b)内,f (x) 0, 则 f () 0, ( ) ( ). 2 1 f x f x y = f (x)在[a,b]上单调增加. 若在(a,b)内,f (x) 0, 则 f () 0, ( ) ( ). 2 1 f x f x y = f (x)在[a,b]上单调减少