
4.罗尔定理的应用 例1f(x)=x2-2x-3=(x-3)x+1). 在-1,3引上连续在(-1,3)上可导,且f(-1)=f3)=0 f'(x)=2(x-1), 取ξ=1,(1∈(-1,3)f'(传)=0
例1 ( ) 2 3 2 f x = x x = (x 3)(x 1). 在[1,3]上连续, 在(1,3)上可导, 且 f (1) = f (3) = 0, 取 = 1, (1(1,3)) f () = 0. f (x) = 2(x 1), 4. 罗尔定理的应用

例2设ao,a1,,a,为实常数,且 a,+g+2+…+a1+a,=0, 23 n+1 证明函数f(x)=a+ax+a2x2+…+anx”1+anx” 在(0,1)内有零点。 证明:作辅助函数 F(x)=a,x+gx2+9x++ 21 3 n n+1
例2 设a0 ,a1 , ,an 为实常数,且0, 2 3 1 1 2 1 0 = n a n a a a a n n 在 内有零点。 证明函数 (0,1) ( ) 1 1 2 0 1 2 n n n n f x = a a x a x a x a x 证明:作辅助函数 , 2 3 1 ( ) 1 2 2 3 1 1 0 = n n n n x n a x n a x a x a F x a x
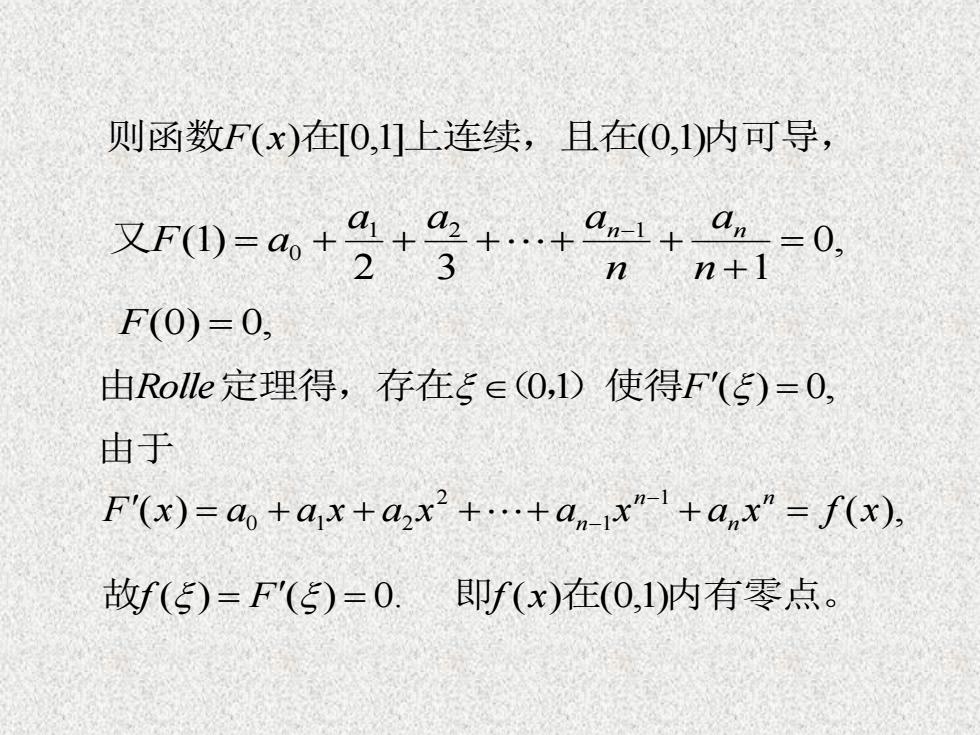
则函数F(x)在0,1]上连续,且在(0,1)内可导, 又)=a+2+号++片=0 3 F(0)=0, 由Roll定理得,存在ξ∈(O,l)使得F'(5)=0, 由于 F'(x)=a+ax+a2x2+.+an-1x”-l+anx”=f(x), 故f(5)=F'(5)=0.即f(x)在(0,1)内有零点
则函数F(x)在[0,1]上连续,且在(0,1)内可导,0, 2 3 1 (1) 1 2 1 0 = = n a n a a a F a 又 n n F(0) = 0, 由Rolle定理得,存在 (0,1)使得F() = 0, ( ) ( ), 1 1 2 0 1 2 F x a a x a x a x a x f x n n n = n = 由于故f () = F() = 0. 即f (x)在(0,1)内有零点

例3证明方程x5-5x+1=0有且仅有一个小于 1的正实根 证设f(x)=x5-5x+1,则f(x)在0,1连续, 且f0)=1,f1)=-3.由介值定理 3x,∈(0,1),使f(x。)=0.即为方程的小于1的正实根. 设另有x1∈(0,1),x≠x,使f(x1)=0. :f(x)在x,x之间满足罗尔定理的条件, ·.至少存在一个5(在x,x,之间),使得 f'(传)=0. 但f'(x)=5(x4-1K0,(x∈(0,1)矛盾, .为唯一实根
例3 1 . 5 1 0 5 的正实根 证明方程 x x = 有且仅有一个小于 证 ( ) 5 1, 5 设 f x = x x 则 f (x)在[0,1]连续, 且 f (0) = 1, f (1) = 3. 由介值定理 (0,1), ( ) 0. x0 使 f x0 = 即为方程的小于1的正实根. (0,1), , 设另有 x1 x1 x0 ( ) 0. 使 f x1 = ( ) , , f x 在 x0 x1 之间满足罗尔定理的条件 至少存在一个 (在 x0 , x1 之间),使得 f () = 0. ( ) 5( 1) 4 但 f x = x 0, (x(0,1)) 矛盾, 为唯一实根

三、Lagranger中值定理 l.Lagrange中值定理 拉格朗日(Lagrange)中值定理 如果函数fx) (1)在闭区间[4,b]上连续; (2)在开区间(a,b)内可导, 那未在(a,b)内至少有一点(a<飞<b),使等式 f(b)-f(a)=f()b-a)成立. 注意:与罗尔定理相比条件怯掉了f()=f(b), 结论亦可写成√b)-f b-0 =f'5)
拉格朗日(Lagrange)中值定理 如果函数 f(x) (1) 在闭区间[a,b]上连续; (2) 在开区间(a,b)内可导, 那末在(a,b)内至少有一点(a b),使等式 ( ) ( ) ( )( ) ' f b f a = f b a 成立. 注 意:与罗尔定理相比条件中去掉了f (a) = f (b). ( ). ( ) ( ) f b a f b f a = 结论亦可写成 三、Lagrange中值定理 1.Lagrange中值定理