3.关于洛尔定理的几点说明 注1:习惯上把结论中的称为中值,罗尔定理的三个条件是充分而非必 要的, 如图,在(a,b)中 y=f(x) 35使f'(5)=0,但 定理的三个条件都 不满足。 x,1x|<1 o a 5b 例如: F(x)= 0,-2≤x≤-1 1,1≤x≤2 易见,F在x=-1不连续,在x=士1不可导,F(-2)≠F(2), 即罗尔定理的三个条件均不成 立,但是在(-2,2)内存在点ξ,满足F'(5)=0
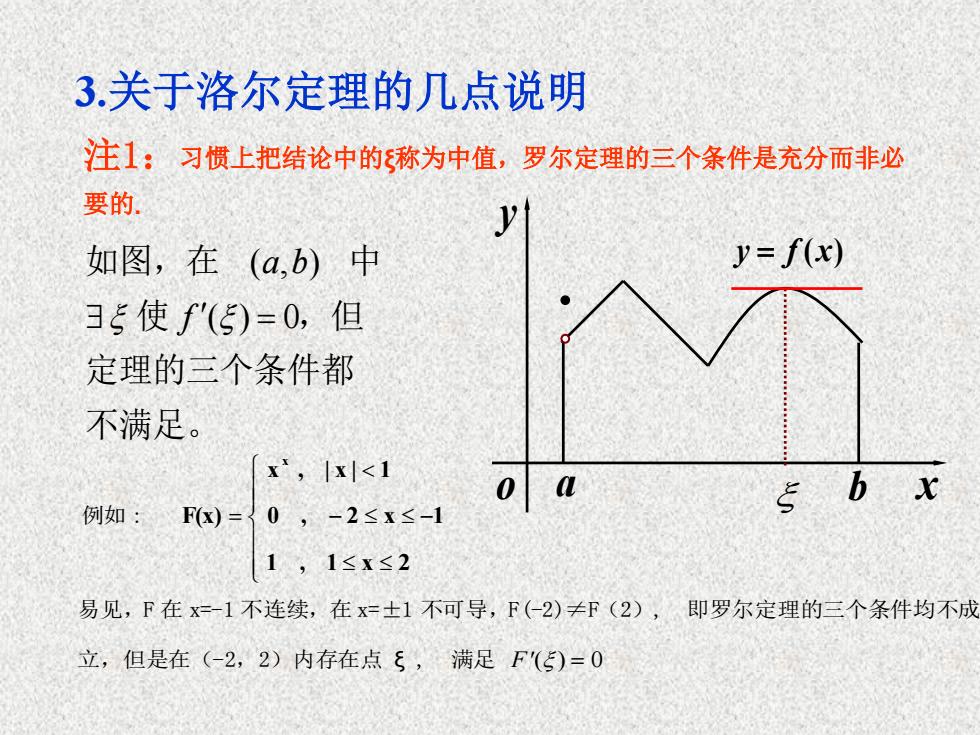
3.关于洛尔定理的几点说明 注1:习惯上把结论中的ξ称为中值,罗尔定理的三个条件是充分而非必 要的. a b x y o y = f (x) 不满足。 定理的三个条件都 使 ,但 如图,在 中 ( ) 0 ( , ) f = a b 例如: = 1 , 1 x 2 0 , 2 x 1 x , | x | 1 F(x) x 易见,F 在 x=-1 不连续,在 x=±1 不可导,F (-2 )≠F(2), 即罗尔定理的三个条件均不成 立,但是在(-2,2)内存在点 ξ , 满足 F( ) = 0
注2:定理的三个条件任意一个不满足,都可能导 致结论不成立。 r0以a专0 ,x=1 3 2 14 f(x)满足条件(2),(3), 0 但不满足条件(1), 在0.D内,Jw=号 图3-1-2
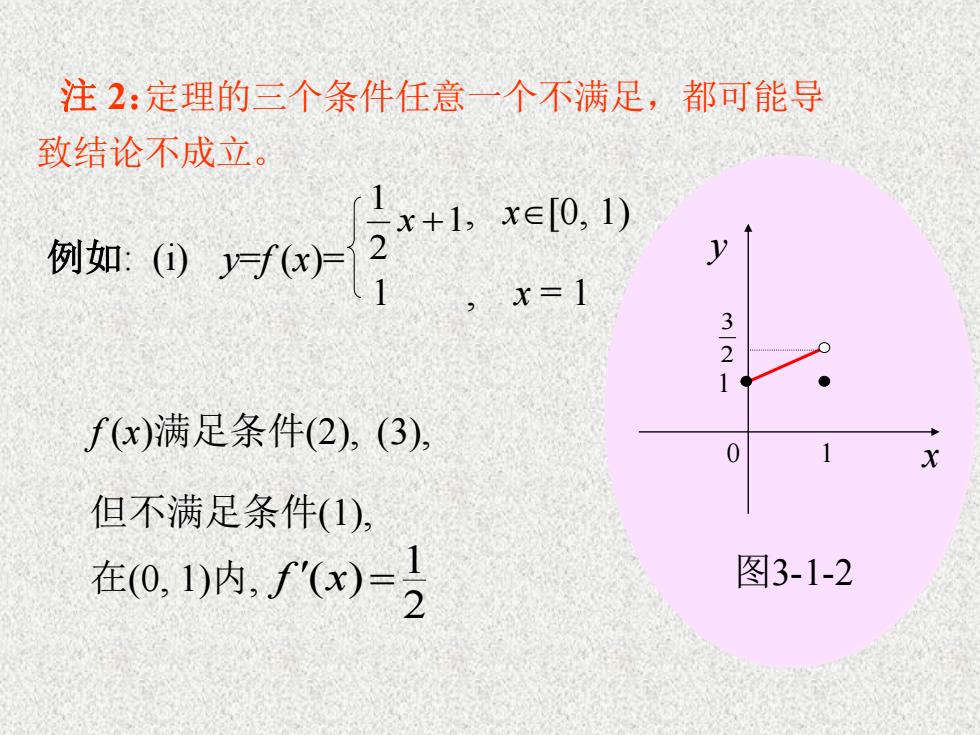
f (x)满足条件(2), (3), 但不满足条件(1), 在(0, 1)内, 2 1 f (x)= 例如: (i) y=f (x)= 1 2 1 x 1 , x = 1 , x[0, 1) 图3-1-2 x y 0 1 1 2 3 致结论不成立。 注 2: 定理的三个条件任意一个不满足,都可能导
(i)y=f(x)x|x∈1, f(x)在[-1,1]上,满足条件(1),(3), 但不满足条件(2), 当x∈(-1,0)时, y=xl f'(x片-1. x∈(0,1)时, f'(x)F1. x=0时, 图3-1-3 ∫‘(0)不存在
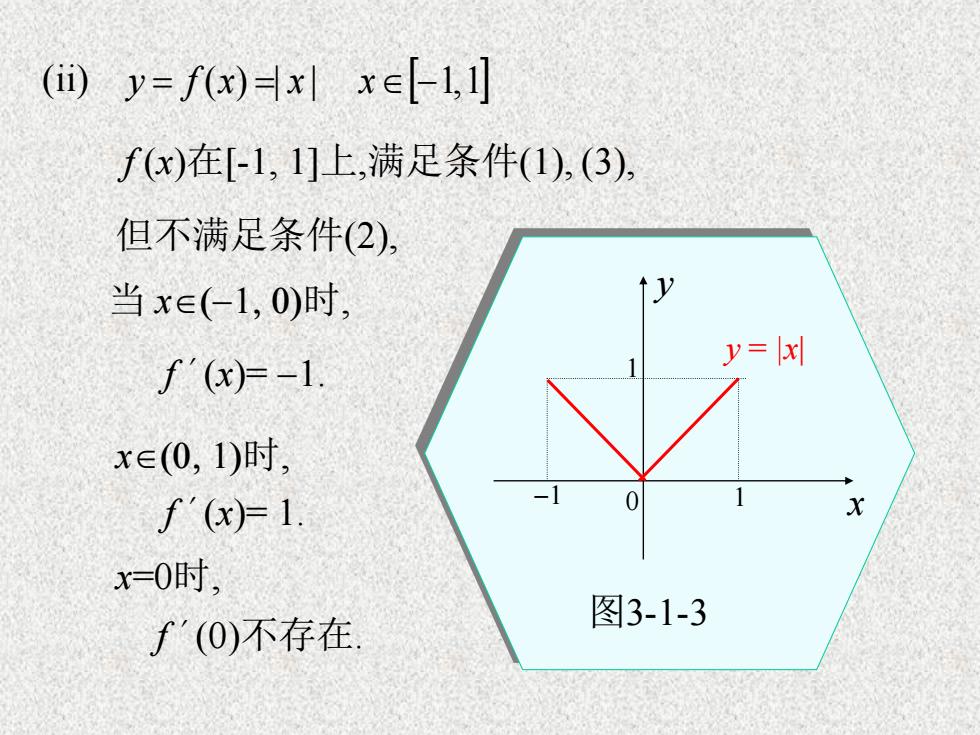
y = f (x) =| x | x1,1 f (x)在[-1, 1]上,满足条件(1), (3), 但不满足条件(2), 当 x 时, f (x)= 1. x 时, f (x)= 1. x=0时, f (0)不存在. (ii) 0 x y 1 1 1 图3-1-3 y = |x|
(ii)y=f(x)=x,x∈[1,2] y 2 f(x)在[1,2]上满足条件 /=x 1 (1),(2) 0 12 但不满足条件(3), 图3-1-4
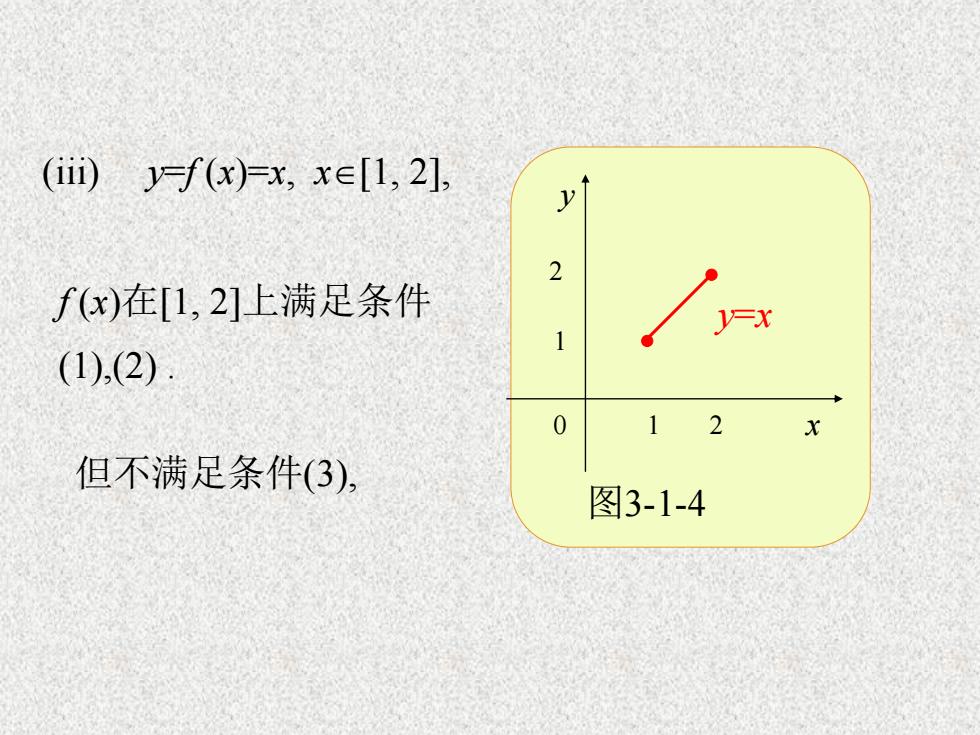
(iii) y=f (x)=x, x[1, 2], f (x)在[1, 2]上满足条件 (1),(2) . 但不满足条件(3), 在(1, 2)内, f (x)=1. 0 2 1 1 2 x y y=x 图3-1-4

注3.罗尔定理的结论中不是唯一的,可能有一个,几个甚至无 穷多个 例如f(x)= xsn2,x≠0 0 x=0 在-1,1]上满足罗尔定理的条件,而显然 J(xr)= 4'sinsin -cos X 0 x=0 在(1,)内,存在无数个c, 2nz 使f(c)=0 注4.将罗尔定理的条件1.2.换为[a,b]上可导,结论仍成立
注3. 罗尔定理的结论中不是唯一的,可能有一个,几个甚至无 穷多个. 例如 4 2 1 sin , 0 ( ) , 0 0 x x f x x x = = 3 2 2 1 1 1 4 sin 2 sin cos , 0 ( ) 0 0 x x x f x x x x x = = 在[-1,1]上满足罗尔定理的条件,而显然 在(-1,1)内,存在无数个 1 2 n c n = 使f / (cn )=0 注4. 将罗尔定理的条件1.2.换为[a,b]上可导,结论仍成立