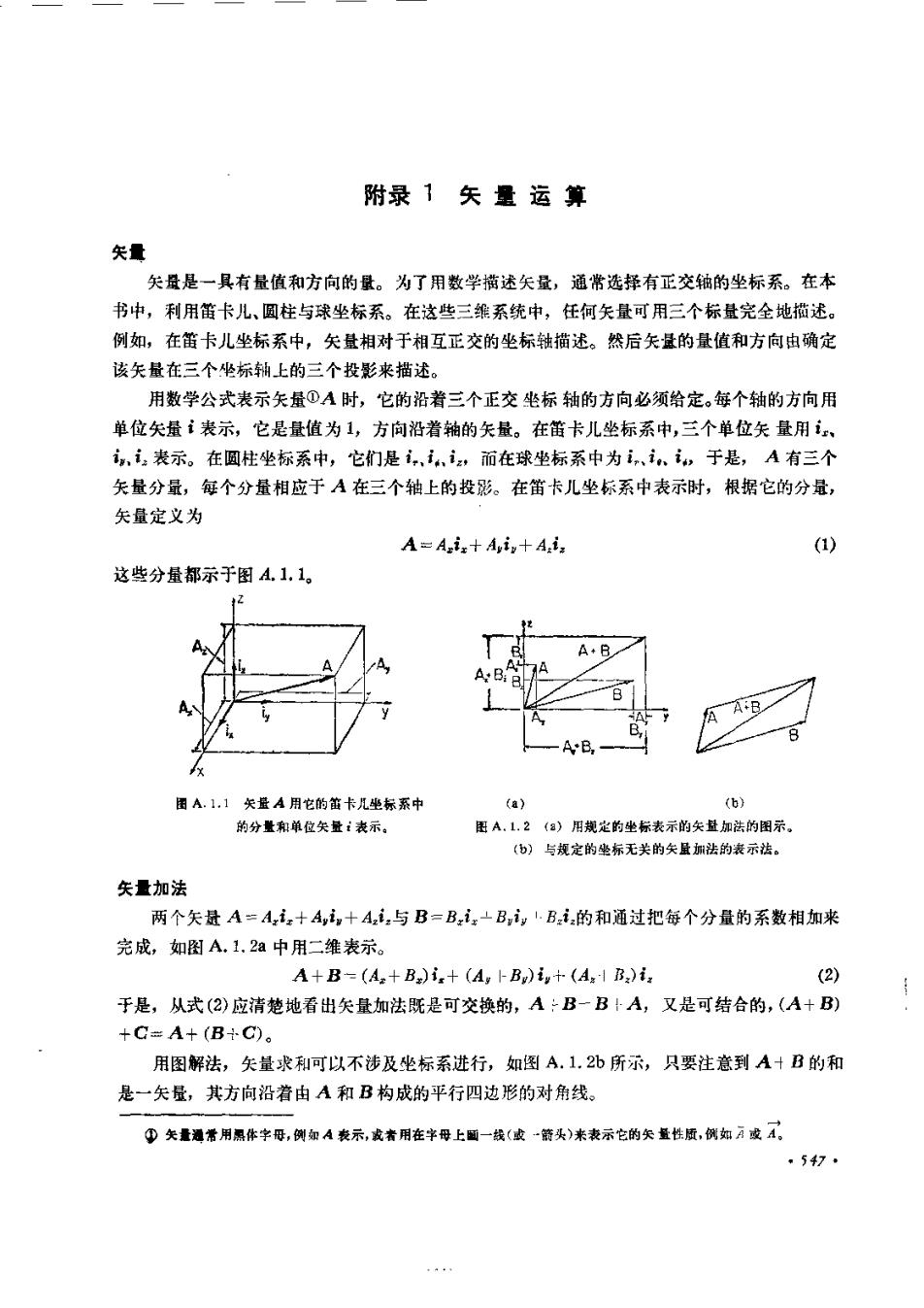
附录1矢量运算失量矢量是一具有量值和方向的量。为了用数学描述矢量,通常选择有正交轴的坐标系。在本书中,利用笛卡儿、圆柱与球坐标系。在这些三维系统中,任何矢量可用三个标量完全地描述。例如,在笛卡儿坐标系中,失量相对于相互正交的坐标轴描述。然后矢最的量值和方向由确定该矢量在三个垒标轴上的三个投影来描述。用数学公式表示矢量①A时,它的沿着三个正交垒标轴的方向必须给定。每个轴的方向用单位矢量i表示,它是量值为1,方向沿着辅的矢量。在笛卡儿坐标系中,三个单位失量用记、诱表示。在圆柱坐标系中,它们是i,、i,而在球坐标系中为,于是,A有三个矢量分量,每个分量相应于A在三个轴上的投影。在笛卡儿坐标系中表示时,根据它的分量,矢量定义为(1)A-Ai+Ain+Ais这些分量都示于图A.1.用东卡毕标系图A.1.2(a)用规定的坐标表示的尖盘加法的图示的分量和单位失量1表示。(b)与规定的坐标无关的失鼠加法的表示法。失量加法两个矢量A=Ai+Ai,+Ai,与B=BiBiBi的和通过把每个分量的系数相加来完成,如图A.1.2a中用二维表示。A+B-(A+B)i+ (A, +B)i,+(AI B)i.(2)于是,从式(2)应清楚地看出矢量加法既是可交换的,AB-BIA,又是可结合的,(A+B+GA+(B+C)。用图解法,矢量求和可以不涉及坐标系进行,如图A.1.2b所示,只要注意到A+B的和是一矢量,其方向沿着由A和B构成的平行四边形的对角线。①失量避滑用黑体字母,例如 A 表示,或者用在字母上买)来表示仑的失盘性质,例如A成1。547

应该注意,矢量用它的分量表示与在哪个坐标系中进行有关。这就是说,坐标系的改变要求适当的失量变换。并且,所用的变量也必须变换,从一个壁标系到另一个坐标系变量和尖量的变换,通过从笛卡儿坐标系到球坐标系的变换来说明。例 1. 2.1 变量与矢最的变换我们给定用z、9和之表示的变量与像A=A,i十4,i+Ai,这样的矢量。我们希望获得用r、0和更表示的变量与表示减A=4,年,十4gi。+Ag。的失量。在图A.1.3a中,我们看到点P有两种表示法,一个与变量r图A.1.3(a)在笛卡儿和球坐标系中,点P的详级说明。图 A.1.4 点积定义的说明。(b)从笛卡儿坐标到球坐标系的变(c)方向的单位矢量到球坐标系的变使和?有关,而另一个与r,和有关。特别是从图A.1.3b,与球坐标的关系为(3)a=rsindcosd用类似的方法,在球垒标系中计算变最和之,可以证明是y=rsinosingO2一805欠量A可以通过把各个单位失段、i,,分解成用球坐标系的单位关员丧示的办法来进行变换。例如,i,可以苔先分解为图A.1.3c 所示的正交坐标系(t、5、2)中的分量。根据定义,沿着Φ一常数和T-平面的交线。 I 也在 α-n 平面内,它垂直于 g-z平面。从而 sind,cos中 和 0 分别是讨沿 z'、9和 z 轴的分量。这些分最依次再分解为沿球坐标方向的分量,认为沿2轴的分量sin中是在i,方向,而沿?轴的分量cost分解为i。方向的分量coscoso和i,方向的分量5sing。这(6)ig=sing cospi,+ cosfcosi,sin pi类似地in=singsindi,+cogo sinpi+coapi8i,cogbi,-sinoi必须强谢,尖导的概念是与坐标系无关的。(在相同的意义上,在第2和4聋中,失量运. 543

筑的定义与表示它们的那个坐标系关。)失量可以形象化为具有方向和量值的带箭头的线元。这个图形使得我们可能用与特定坐标系的选择无关的几何的语言来处理尖量,现在就用它来定之最重要的失量运算。为了解析的或数值的目的,运算一般用坐标表示法进行。于是,如所述的,在本书后商部分或在习题中,每一种运算都将在笛卡儿坐标系中计算。标量积的定义给定如图A.1.4中所示的欠量A和B,两个矢量间的标量积或点积定义为(9)A·B-(A|IBIcosg武中e是两个矢量间的夹角。从它的定义可直接得出标积是可交换的。A·B-B.A(10)标量积也是可分配的。(A+B).C=A.C+B.C(11)要看出这点,注意到A.C 是A在C上的投影乘以C的量值ICI,而BC是B在C上的投影乘以ICI。因为投影是可相加的,就得到(11)式这两个性质可以用来利用管卡儿坐标系中欠录的分量确定标量积。接照单位失量的定义,ii-ii-ii-l-ii0(12)当A和B用它们的分量表示时,从分配性和交换性可得(13)A.B=AB++AB,+ AB.因此,按照式(9),矢最量值的平方是A·A=|A}"=A+A+A(14)失量积的定义矢量 A 和 B的叉积是一个矢量 C,它的量值是G|-|Al|B|sing(15)而方向与A和B都垂直。几何学上,的量值就是由矢量A和B构成的平行四边形的面积。矢量C有右螺旋前进的方向,好像是由将A旋转到B来驱动的。换句话说,右手坐标系由A-B-C构成,如图A.1.5中所示。叉积通常采用的标记法是C-AxB(16)注态到如果把尖量A分解为两个相互垂直的欠量,,A=A1+A,是有用的,式中A位于A和B的平面内并且垂直于B,而A,平行干B,则A×B-AI×B(17)此等式从这一事实得出,这两个叉积有同样的量值(由于|AI×B=IAIIB|和|A|IA/sing)和方向(垂直于A和B)。叉积的分配性质,·549

C-AXB丽积IC义的说明(A+B)×D=AxD+BxD(18)可以用式(17)证明,并且图A.1.6的几何解释如下。首先,注意(A--B)1=(AI+B),式中工表示分别在A和D的平面内或B和D的平面内的分量,并且垂直于D。这样(19)(A+B)×D=(A+B)+×D=(AI+B) ×D现在,我们只需要证明(20)(A+B)×D-=AI×D+B×D在图A.1.6中用矢量AI、B,和它们的和给出这个方程的图解表示。在IDI倍的范围内,三个尖正A_×D,BI×D和它们的和分别是将欠量A、B和它们的和旋转90度。因此,对A1+B.已经证明的失量加法性质,也适用于AI×D+B,×D因为交换两个矢量的次序需要重新指定叉积失量的方向(图A.1.5中C的方向),这里可交换性不成立。相反地,(21)AxB=-BxA利用分配律,两个失量的矢量积可以根据它们的笛卡儿坠标,利用单位失献的尖量积的下列性质构成ixi-0 ixii.(22)i,xi,-0 ixi.--ixi,-iixi,-o ixi"--ixi--i因此AxB -i(A,B-AB)+i,(A.B-A,B)(23)-i(AB--A,B,)在简卡儿坐标系中求叉积的有用的记忆法可以通过将(23)式的有边记成矩陈的行列式来实现:iiAxB:AA, A.(24)BBuB.标量三重积关量A,B和C的标量三重积的定义可根据图A.1.7以及标是积和欠量积的定义得出。550

(25)A.(BxC)=-IA/cos (A, B×G)IIBICI sin (B,C))标最三重积等于以三个矢量为其三个基面的平行六面体的体积。即在(25)式中,第二个方括号中的项是图A.1.7中平行四边形底面的面积,而第一项是平行六面体的高度。如果根期这三个失量书写的顺序,它们构成右手坐标系,这个标量三重积是正的;否侧就是负的。因而,循环地重新排列失量的顺序,能使三重积的值保持不变。(26)A.(BxG)=B(CXA)-G.(A×B)由此得出在标量三重积中叉和点的位置可以是任意的,又和点可以相互交换而不致影响乘积。利用在笛卡儿巫标系中计算点积和叉积的规则,我们有(27)A-(B×G) -A(B,C, -B,C) +Ay(B,C,-B,C,)+A(BC-BC.)图 A.1. 8 双重又积的图期衰示,图A,1.7标量三重积的图解表示。双重叉积考虑矢量积A×(B×C)。是否存在另外一种有时是更为有用的表示这个双重叉积的方式由于积B×C垂直于由 B和 C 确定的平面,则最后的积 A×(B×C)一定位于 B和 C 的乎面内。因此,矢量积一定可以表示成矢量B 和 C 的线性组合。求此线性组合的系数的一个方法是在笛卡儿坐标系中计算这个积。但这里我们宁愿利用几何的推导。因为量B×C垂直于由B和C确定的平面,由图A.1.7可得(28)A×(B×C) =A'×(B×G)式中A'是A在由B和C确定的平面上的投影。其次,我们将失量C分解成平行于B的分量C和垂直于B的分量C,如图A,1.8所示,因此(29)A×(B×C)=A×(B×C)然后,按照又积的性质,矢量积的量值由A×(B×C)/=|ATIB|IC)(30)给出,而失量积的方向是与A'正交并位于由矢量B和 确定的平面内,如图A.1.8所示。在a-多平面内构筑一个垂直于已知矢量A的欠量的规则如下。首先,确定相对于任意两个正交轴(z,)的A'的分量。这里它们是CI和B的方向,分别有分量A'.C,和 A" B。然后通过交换和 !分量并且改变其中一个的符号来构筑一新的欠量。按照这个规则,图 A.1.8表明矢量A×(B×G)由·551