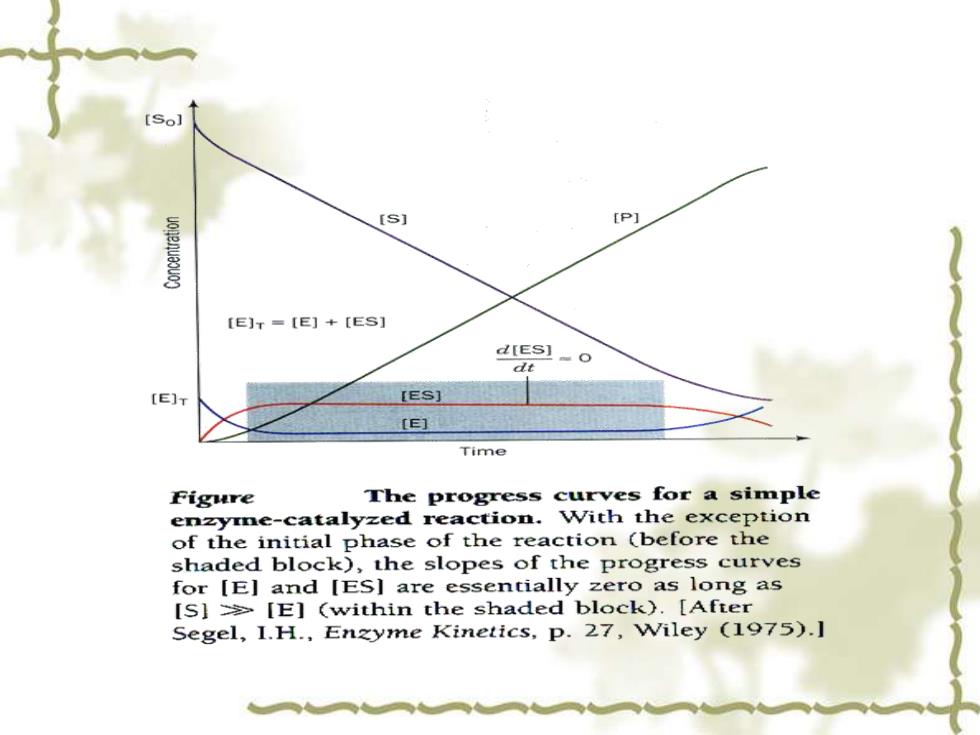
Sol [s] [P] [E]r=【E]+[ES】 des】-o dt [E]T 【ES] [E] Time Figure The progress curves for a simple enzyme-catalyzed reaction.With the exception of the initial phase of the reaction (before the shaded block),the slopes of the progress curves for[E】and【Es】are essentially zero as long as [S][E](within the shaded block).[After Segel,I.H.,Enzyme Kinetics,p.27,Wiley (1975).I
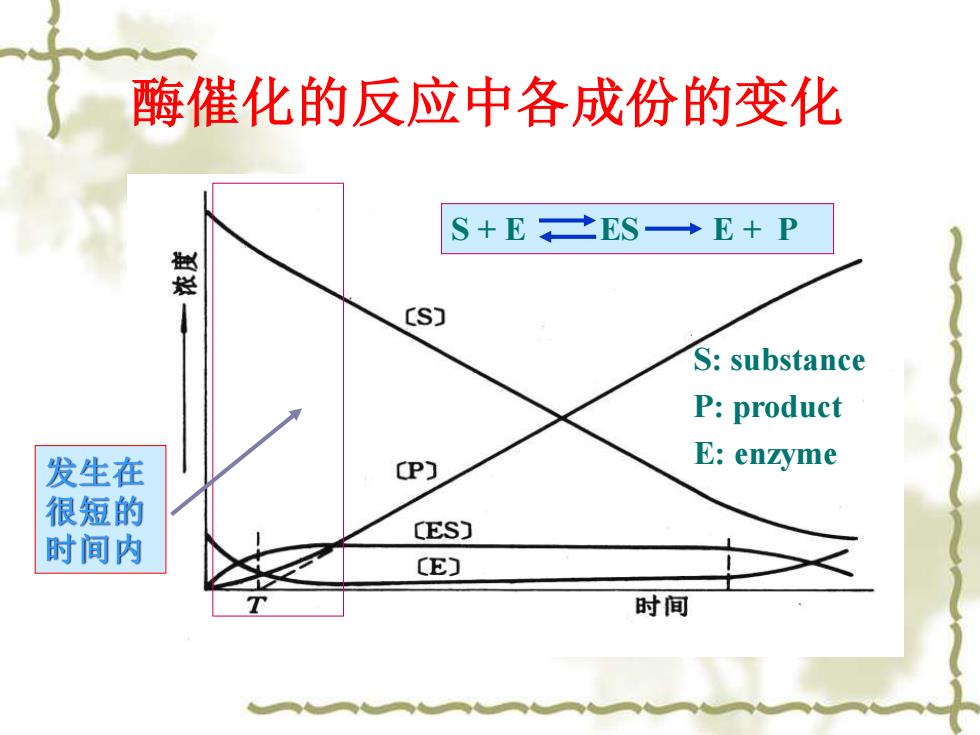
酶催化的反应中各成份的变化 S+E±ES→E+P 烂 (S) S:substance P:product 发生在 (P) E:enzyme 很短的 CES] 时间内 CE) 时间
酶催化的反应中各成份的变化 S + E ES E + P S: substance P: product E: enzyme 发生在 很短的 时间内

Michae.1is-Menten方程(1925年) Briggs&Haldane?重新推导 E+S÷Es芒P+E k1([Et]-[ES])[S]=k2[ES]+k3[ES] k2+k3 (Et]-[ES])[S] k1 [ES] Km=(k2+k3)/k1,[ES][Et][S]/(Km [S]) 因为V=k3[ES],而Vmax=k3[Et灯 因此v=Vmax[S]/(Km+[S])
Briggs & Haldane重新推导 E + S ES P + E k1([Et]-[ES])[S] = k2[ES] + k3 [ES] k2 + k3 ([Et]-[ES])[S] k1 [ES] 令Km=(k2+k3)/k1, [ES] = [Et][S]/(Km + [S]) 因为 v = k3[ES], 而 Vmax = k3[Et] 因此 v = Vmax [S]/(Km + [S]) Michaelis-Menten方程(1925年) k1 k2 k3 k4 =

米氏方程的推导 S+E ES k→P+E 时E-E网 网 [ES]生成速度: Y=k(①E,]-[ES]S] [ES]分解速度: V2 =klES]+k2 [ES] 当酶反应体系处于恒态时:V1=V2 即: k (E,]-[ES)IS]=k[ES]+k [ES] >E,[S]-[ES][S]_k1+k2 ES k
1 1 2 k k k ES Et S ES S + = − − S + E ⎯ ⎯⎯k1 ⎯→ −1 k ES ⎯⎯k2 → P + E E ES t S − ES [ES]生成速度: v k (E ES)S 1 = 1 t − [ES]分解速度: v k ES k ES 2 = −1 + 2 即: k (E ES)S k ES k ES 1 t − = −1 + 2 → 当酶反应体系处于恒态时: v1 = v2 米氏方程的推导

令:+k=Km 则:Km[ES]+[ESS]=ES] k 经整理得:=《的 [E,Is] (1) 由于酶促反应速度由[BS]决定,即v=k[ES(2) k2 [E,IS] 将《①D代入(2)得:V=K+卤 (3) 当[Et]=[ES]时,v=Vm所以Vm=k[E,] (4) 将(4)代入(3),则:v= Viax [S] K+[S]
令: Km k k k = − + 1 1 2 将(4)代入(3),则: 则: K ES ESS S m + = Et 经整理得: K S E S m t + ES = 由于酶促反应速度由[ES]决定,即 v k ES = 2 K S k E S m t + = 2 v 当[Et]=[ES]时, v =Vm m Et V k 所以 = 2 K S V S v m + = max (2) (1) 将(1)代入(2)得: (3) (4)