
第四节 多元面数微分学的应用 一、空间曲线的切线与法平面 二、空间曲面的切平面与法线 三、多元函数的极值 HIGH EDUCATION PRESS 返回结束
第四节 复习 目录 上页 下页 返回 结束 一、空间曲线的切线与法平面 二、空间曲面的切平面与法线 多元函数微分学的应用 三、多元函数的极值
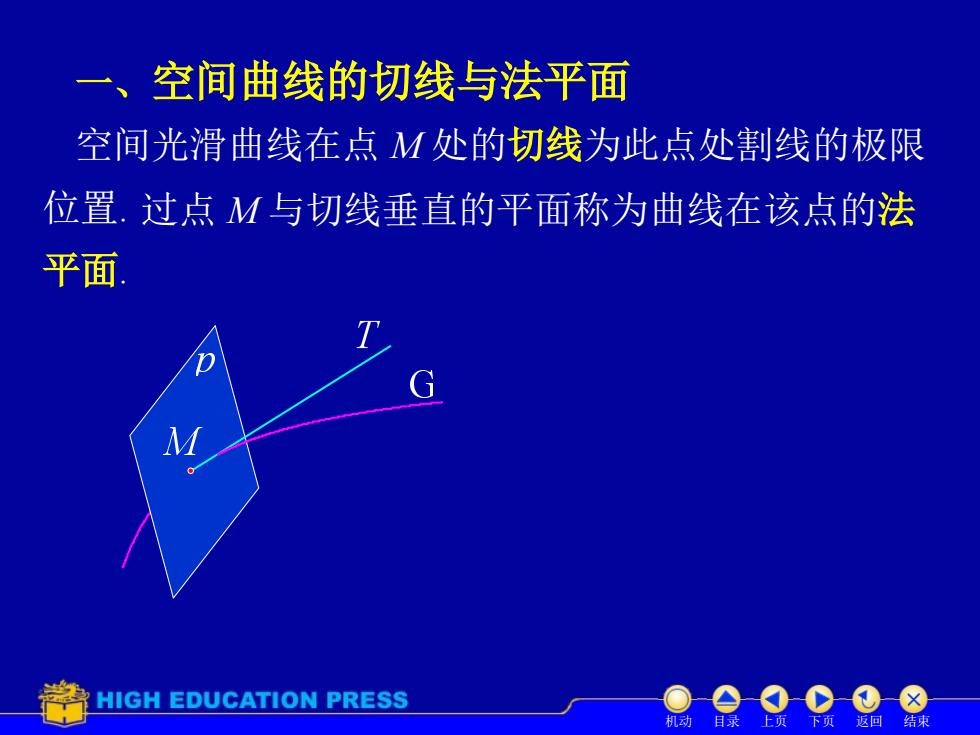
一、空间曲线的切线与法平面 空间光滑曲线在点M处的切线为此点处割线的极限 位置.过点M与切线垂直的平面称为曲线在该点的法 平面 HIGH EDUCATION PRESS 机动 返回 结
一、空间曲线的切线与法平面 过点 M 与切线垂直的平面称为曲线在该点的法 机动 目录 上页 下页 返回 结束 位置. 空间光滑曲线在点 M 处的切线为此点处割线的极限 平面

1.曲线方程为参数方程的情况 G:x=j(t),y=y(1),z=w(1) 设t=t0对应M(x0,y0,2o) 切线的方向向量: T=0)yo),wto)》 称为曲线的切向量 HIGH EDUCATION PRESS 机动目录
机动 目录 上页 下页 返回 结束 1. 曲线方程为参数方程的情况 切线的方向向量: 称为曲线的切向量

G:x=j(),y=y(0,2=w(0 设t=t0对应M(x0,y0,o) 曲线的切向量:T=(o),yto),wo) 切线方程 x-0=y-Y0=2-20 ito)v cto)w(to) 法平面方程 i0)(x-x)+y4)y-yo)+w0(2-z0)=0 HIGH EDUCATION PRESS
曲线的切向量: 法平面方程 切线方程

例1.求圆柱螺旋线x=acos1,y=asint,z=b(a,biR,a10,b10) 在1=号对应点处的切线方程和法平面方程 HIGH EDUCATION PRESS 机动自录项
例1.求圆柱螺旋线 在 对应点处的切线方程和法平面方程. 机动 目录 上页 下页 返回 结束