
第三为 复合求导、隐品数求导及方向导数 一元复合函数y=f(),=j(x) 求导法则 dy dy du dx du dx 本节内容: 多元函数复合求导、隐函数求导 HIGH EDUCATION PRESS
第三节 一元复合函数 求导法则 本节内容: 多元函数复合求导、隐函数求导 机动 目录 上页 下页 返回 结束 复合求导、隐函数求导及方向导数
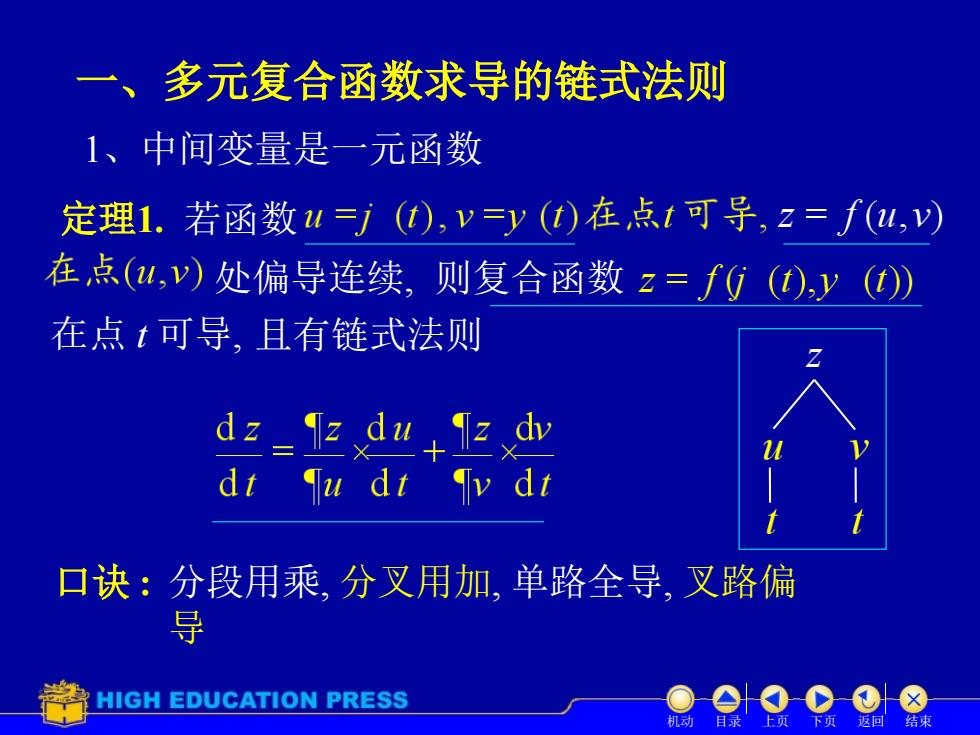
一、多元复合函数求导的链式法则 1、中间变量是一元函数 定理1.若函数w=j(),v=y(t在点1可导,z=f(u,v) 在点(u,v)处偏导连续,则复合函数z=f0(),y(t) 在点t可导,且有链式法则 dz du dt Ju dt Iv dt 口诀:分段用乘,分叉用加,单路全导,叉路偏 导 HIGH EDUCATION PRESS
一、多元复合函数求导的链式法则 定理1. 若函数 处偏导连续, 在点 t 可导, 则复合函数 且有链式法则 机动 目录 上页 下页 返回 结束 口诀 : 分段用乘, 分叉用加, 单路全导, 叉路偏 导 1、中间变量是一元函数

推广:设下面所涉及的函数都可微 1)中间变量多于两个的情形.例如,z=f(u,V,w), u=j(),v=y(t),w=w(t)复合得 复合函数z=f()y(),w()] dz=z+2d业+2dw dt u dt Iv dt w dt HIGH EDUCATION PRESS 动 目录
推广: 1) 中间变量多于两个的情形. 例如, 设下面所涉及的函数都可微 . 机动 目录 上页 下页 返回 结束 复合得 复合函数

例1.设z=m,1=e,v=cosL,求 dt dz 例2.设z=ln(u+)+e,u=21,v=12,求 di HIGH EDUCATION PRESS 凯动 自录 上页 下方 返回 结球
例1. 设 机动 目录 上页 下页 返回 结束 求 例2. 设 求

2)中间变量是多元函数的情形 (多元函数与多元函数的复合) 定理2 z=f(u,v),u=j (x,y),v=y (x,y) 复合函数z=(x,)y(x,y)] E=Exux Ix J 9x fv 9x 1=1xux Iy Ju Iy v Ty HIGH EDUCATION PRESS
2) 中间变量是多元函数的情形. (多元函数与多元函数的复合) 定理2. 机动 目录 上页 下页 返回 结束 复合函数