
3.2.1系统内部稳定性的基本概念 (1)李亚普诺夫意义上的稳定性(is.L稳定性) ·定义:如果对于给定的任意实数ε>0,都对应地存在另一实 数6(6,o)>0,使系统满足 |x-x≤8e,) (3-11) 的任一初始状态的响应都满足 pG,o,xo,0)-xe≤e t≥to (3-12) 则平衡状态x。是李雅普诺夫意义上稳定的,简记为is.L稳定。 若6只依赖于ε,而和初始时刻无关,则称平衡状态x。 为一致稳定的。 若ε→0((整个状态空间),则x是大范围稳定的
3.2.1 系统内部稳定性的基本概念 ⑴ 李亚普诺夫意义上的稳定性 ( 稳定性) i.s.L 定义: 如果对于给定的任意实数 ,都对应地存在另一实 数 ,使系统满足 ε > 0 0 δ(ε,t 0)> ( , ) 0 0t e x − x ≤ δ ε 的任一初始状态 的响应都满足 x0 − ≤ ε e φ(t;t , x ,0) x 0 0 0 t ≥ t 则平衡状态 是xe 李雅普诺夫意义上稳定的,简记为 稳定。 i.s.L 若 只依赖于 ,而和初始时刻 无关,则称平衡状态 为一致稳定的。 若 (整个状态空间),则 是大范围稳定的。 δ ε • (3-12) (3-11) xe xe ε → ∞ 0t

·线性系统is.L稳定 对线性系统)=Ax0,如果由有限的初始状态x)=x。引起 的零输入响应是有界的,则称系统是李亚普诺夫意义上的 稳定。 设系统由有限的初始状态 ‖x≤6 6是一个实数 引起的系统的零输入响应满足 ‖p(tto,xo,0)≤e £是一个实数 (3-13) 则系统是is.L稳定。 线性定常系统中出现的等幅振荡是iL稳定的,工程上认为 是一种临界稳定
线性系统 稳定 对线性系统 ,如果由有限的初始状态 引起 的零输入响应是有界的,则称系统是李亚普诺夫意义上的 稳定。 i.s.L x &(t) = Ax(t) 0 0 x(t ) = x 设系统由有限的初始状态 0 x ≤ δ δ 是一个实数 引起的系统的零输入响应满足 φ( ; , x ,0) ≤ ε 0 0 t t ε 是一个实数 则系统是 稳定。 i.s.L 线性定常系统中出现的等幅振荡是 稳定的,工程上认为 是一种临界稳定。 i.s.L • (3-13)

图3一2是李亚普诺夫意义上稳定的示意图。 对任意ε>0,存在几何意 Sc)球域 义上的球体,将此球域记为 se)。若对应地存在6(6,)>0 S(8)球域 其球域为so)。在s()内的初 始状态x。,如其1≥,的轨线 p(to,x。,0)均不超过Se),则 平衡状态x。在李亚普诺夫意 义上是稳定的。 图3-2
图3-2是李亚普诺夫意义上稳定的示意图。 图3-2 对任意 ,存在几何意 义上的球体,将此球域记为 。若对应地存在 , 其球域为 。在 内的初 始状态 ,如其 的轨线 均不超过 ,则 平衡状态 在李亚普诺夫意 义上是稳定的。 ε > 0 S(ε ) 0 δ(ε,t 0 )> S(δ ) S(δ ) xe 0 t ≥ t ( ; , ) φ t t0 x e ,0 S(ε ) xe xe = 0 0 x S(δ )球域 S(ε )球域 a x b x

(2)渐近稳定 ·定义如果平衡状态x是isL稳定的,且对给定的实数 6(&,)>0和“>0,存在T(4,6,t),使系统由|x-x≤e,t) 的x引起的零状态响应均满足 p(tto,xo,0)-x≤4 t≥t+T(4,δ,t) (3-14) 随着T→∞,有4→0 lim o(t;to,x,0)=0 (3-15) t00 则称平衡状态x。在,时刻为渐近稳定的。 。若对任意时刻t。均渐近稳定,那麽,x,为一致渐近稳定的。 若对于任意的x,其响应均满足im(Go0=0,则称x。 为大范围渐近稳定(也称全局渐近稳定)。 ● 对线性系统)=A()x():唯一的平衡状态x。=0,如果是 渐近稳定的,必是大范围渐近稳定的。 ● 对线性定常系统)=A()x):稳定性与初始时刻无关, 如果是渐近稳定的,必是一致大范围渐近稳定的
⑵ 渐近稳定 定义 如果平衡状态 是 稳定的,且对给定的实数 和 ,存在 ,使系统由 的 引起的零状态响应均满足 e x i.s.L δ(ε,t 0)> 0 μ > 0 ( , , ) 0 T μ δ t ( , ) 0 0t e x − x ≤ δ ε x0 ( ; , ) ( , , ) 0 0 0 0 t t t t T t φ x ,0 − xe ≤ μ ≥ + μ δ 随着 ,有 T → ∞ μ → 0 φ x 0 = 0 →∞ lim ( ; , , ) 0 0 t t t 则称平衡状态 在 时刻为渐近稳定的。 x0 若对任意时刻 均渐近稳定 ,那麽, 为 t0 一致渐近稳定的。 若对于任意的 ,其响应均满足 ,则称 为大范围渐近稳定(也称全局渐近稳定)。 0 • x xe • • (3-14) φ x ,0 = 0 →∞ lim ( ; , ) 0 0 t t t (3-15) • 对线性系统 :唯一的平衡状态 ,如果是 渐近稳定的,必是大范围渐近稳定的。 x &(t) = A(t)x(t) xe = 0 • 对线性定常系统 :稳定性与初始时刻无关, 如果是渐近稳定的,必是一致大范围渐近稳定的。 x &(t) = A(t)x(t) 0t x0
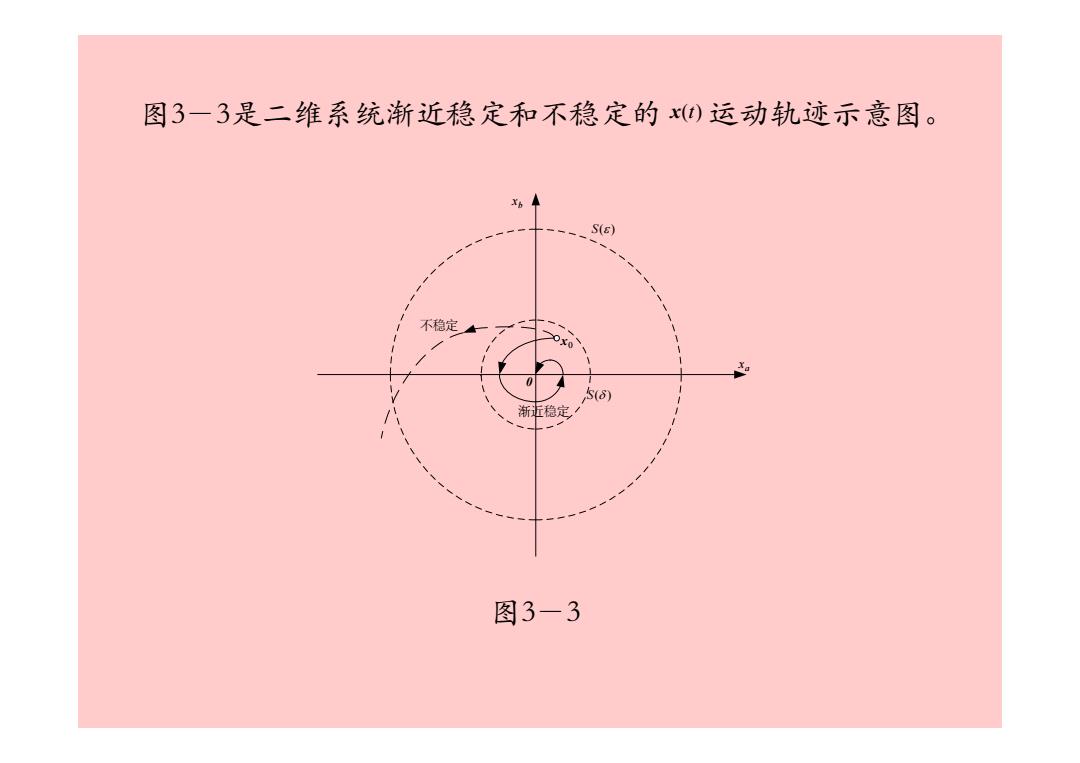
图3一3是二维系统渐近稳定和不稳定的x()运动轨迹示意图。 S(s) 不稳定 00 0 渐稳定 图3-3
0 0 x S(δ ) S(ε ) a x b x 渐近稳定 不稳定 图3-3是二维系统渐近稳定和不稳定的 运动轨迹示意图。 x(t) 图3-3