
3.2系统的内部稳定性 系统的内部稳定性是研究系统的零输入响应的稳定性。因 此只要讨论齐次状态方程 =f(x,t) x(to)=xo,t≥to (3-4) 由初始状态x(t)=x引起的响应的稳定性,是状态稳定性问题。 (1)系统的平衡状态 对定常系统,齐次状态方程为 =A(t)x x(to)=xo,t≥to (3-5) 如果系统所处的状态x满足 x。=0 这个状态称为平衡状态。 由平衡状态的定义,不会使系统产生运动,即 o(t;to,xc,0)=x. (3-8)
3.2 系统的内部稳定性 系统的内部稳定性是研究系统的零输入响应的稳定性。因 此只要讨论齐次状态方程 0 0 0 x& = f ( x,t ) x ( t ) = x ,t ≥ t 由初始状态 引起的响应的稳定性,是状态稳定性问题。 0 0 x ( t ) = x ⑴ 系统的平衡状态 对定常系统,齐次状态方程为 0 0 0 x& = A(t)x x(t ) = x ,t ≥ t 如果系统所处的状态 满足 e x x& e = 0 这个状态称为平衡状态 。 e x e e φ(t;t0 , x ,0) = x 由平衡状态的定义, 不会使系统产生运动,即 (3-4) (3-5) (3-7) (3-8)

平衡状态的计算 平衡状态x。为下列方程的解 x。=f(xe,t)=0 对线性定常系统,。满足 x。=Ax。=0 (3-9) ·当A为非奇异时,上述方程有唯一零解x.=0,即系统的零状 态(原点)是系统的唯一平衡状态。 。当A为奇异时,上述方程有无穷多解。对于任意一个已知的 平衡点,总可以通过坐标变换将它转移到原点,所以通常总 是将系统的平衡状态定在零状态。 ·对渐近稳定系统,A总是非奇异的,零状态(原点)是系统的 唯一平衡状态
平衡状态的计算 平衡状态 为下列方程的解 e x x & e = f (xe ,t) = 0 对线性定常系统, 满足 e x x = Ax = 0 e e & 当 为非奇异时,上述方程有唯一零解 ,即系统的零状 态(原点)是系统的唯一平衡状态。 A xe = 0 当 为奇异时,上述方程有无穷多解。对于任意一个已知的 平衡点,总可以通过坐标变换将它转移到原点,所以通常总 是将系统的平衡状态定在零状态。 A 对渐近稳定系统, 总是非奇异的,零状态(原点)是系统的 唯一平衡状态。 A • • • (3-9)

例3一2倒立摆系统 系统的齐次状态方程为 *7 1 0 2 0 0 -1 0 X2 0 0 0 1 0 0 11 0x4 显然,A是奇异的,齐次状态方程有无穷多个解。从系统 的状态转移矩阵 11 -B2 -B3 01 -1-11B3 -B2 00 1+11p2 1+11B3 0011+1213 1+11p2」 可知,任一[x1000]都是平衡状态,因为只要其他状态 的初值为零,系统将始终稳定在(小车的位移)的初始位 置x0上
例3-2 倒立摆系统 系统的齐次状态方程为 ⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ − =⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ 4321 4321 0 0 11 0 0 0 0 1 0 0 1 0 0 1 0 0 xxxx xxxx&&&& 显然, 是奇异的,齐次状态方程有无穷多个解。从系统 的状态转移矩阵 A ⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ + + + + − − − − − = 3 2 2 3 3 2 2 3 0 0 11 121 1 11 0 0 1 11 11 0 1 11 1 β β β β β β β β t t t t e At 可知,任一 都是平衡状态,因为只要其他状态 的初值为零,系统将始终稳定在 (小车的位移)的初始位 置 上。 10 x 1x T [ x 0 0 0 ] 1
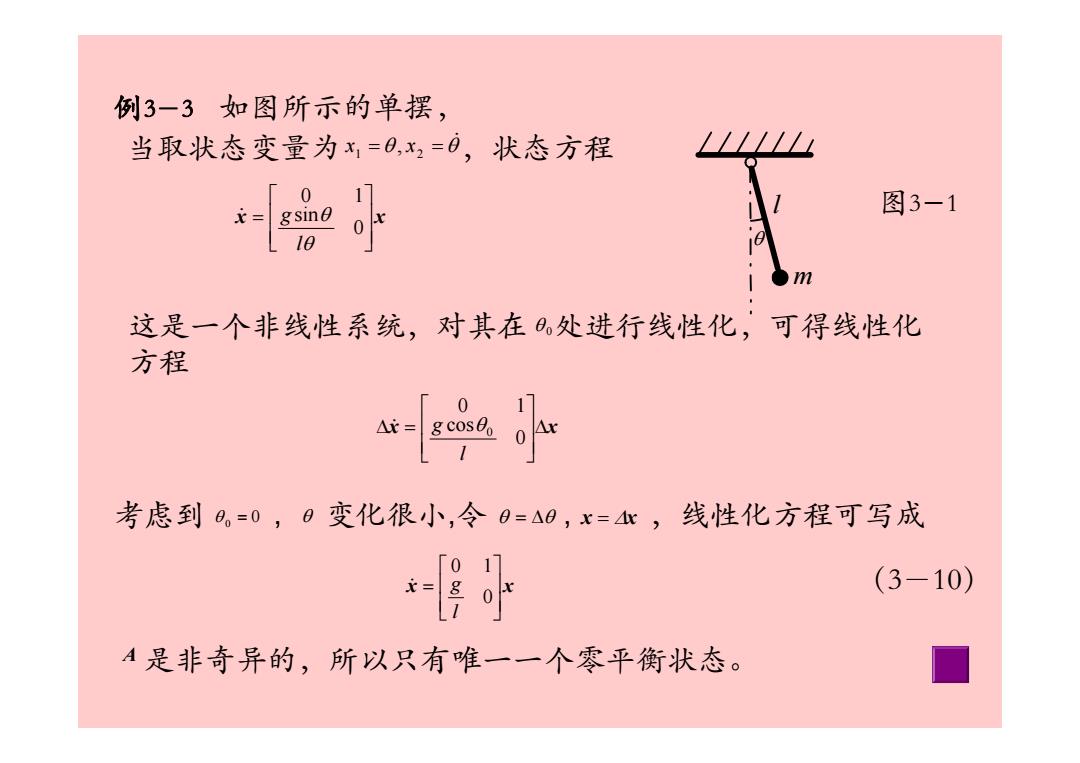
例3一3如图所示的单摆, 当取状态变量为,=日,2=0,状态方程 0 1 图3-1 L10 这是一个非线性系统,对其在处进行线性化,可得线性化 方程 「0 11 考虑到日,=0,日变化很小,令日=△8,x=,线性化方程可写成 「01 (3-10) A是非奇异的,所以只有唯一一个零平衡状态。 ■
例3-3 如图所示的单摆, l m θ 当取状态变量为 ,状态方程 θ θ& x1 = , x2 = x x⎥⎥⎦⎤ ⎢⎢⎣⎡ = 0 sin0 1 θθl & g 这是一个非线性系统,对其在 处进行线性化,可得线性化 方程 θ 0 x x⎥⎥⎦⎤ ⎢⎢⎣⎡ = 0 0 1 l & g x Δx ⎥⎥⎦⎤ ⎢⎢⎣⎡ Δ = 0 cos0 1 0 l & g θ 考虑到 θ 0 = 0 , θ 变化很小,令 θ = Δθ , x = Δx ,线性化方程可写成 A 是非奇异的,所以只有唯一一个零平衡状态。 图3-1 (3-10)

系统的内部稳定性就是研究当系统受到扰动而偏离平衡状 态后,能否返回平衡状态,或者回到离原平衡状态的一定范 围内,因此系统内部稳定性就是指系统平衡状态的稳定性。 下面将系统平衡状态的稳定性简称为系统的稳定性
, 系统的内部稳定性就是研究当系统受到扰动而偏离平衡状 态后,能否返回平衡状态,或者回到离原平衡状态的一定范 围内,因此系统内部稳定性就是指系统平衡状态的稳定性。 下面将系统平衡状态的稳定性简称为系统的稳定性