
机器人智能系统实验指导书 #

倒立摆实验设备简介 6 7 8 9 6 11 10 12 8 13+ 14 3 9 QUANSER ⊙ COM LabViEW
倒立摆实验设备简介

编号 说明 备注 1 直流电机 死区电压约为0.5V~1.5V 2 臂杆角度测量高精度编码器 3 电机金属支架 4 旋转臂杆转轴 5 旋转臂杆 6 摆杆编码器 7 摆杆转轴 8 摆杆 摆杆质量块 10 ELVIS-l插卡金手指 11 QNET倒立摆PWM和编码器信号接口板 12 QNET倒立摆24V电源插头 给电机PWM驱动器供电 13 熔丝 250V,3A 14 电源指示灯 +B,+15V,-15V,+5V 实验主要内容: 1.控制对象建模与分析 2.控制算法设计与仿真 3.自平衡控制算法设计及参数优化 实验准备及注意事项 ·先仔细阅读操作说明 注意装置的通、断电顺序 旋转倒立摆有机械运动部件,实验时务必注意安全 注意逐步选择合适的控制参数,避免设备受损 注意在合适的臂杆角度位置开始实验,避免导线缠绕 软件环境 LabVIEW 2012 ELVISmx Control Design and Simulation Module Quanser Engineering Trainer(QNET)module Acrobat Reader(pdf) 硬件环境 ELVIS-ll+with power supply - QNET ROTPENT with power supply PC platform with USB2.0 预备知识 -LabVIEW编程 自动控制原理:动态系统建模与分析 控制算法设计
编号 说明 备注 1 直流电机 死区电压约为 0.5V~1.5V 2 臂杆角度测量高精度编码器 3 电机金属支架 4 旋转臂杆转轴 5 旋转臂杆 6 摆杆编码器 7 摆杆转轴 8 摆杆 9 摆杆质量块 10 ELVIS‐II 插卡金手指 11 QNET 倒立摆 PWM 和编码器信号接口板 12 QNET 倒立摆 24V 电源插头 给电机 PWM 驱动器供电 13 熔丝 250V, 3A 14 电源指示灯 +B, +15V, ‐15V, +5V 实验主要内容: 1. 控制对象建模与分析 2. 控制算法设计与仿真 3. 自平衡控制算法设计及参数优化 实验准备及注意事项 ‐ 先仔细阅读操作说明 ‐ 注意装置的通、断电顺序 ‐ 旋转倒立摆有机械运动部件,实验时务必注意安全 ‐ 注意逐步选择合适的控制参数,避免设备受损 ‐ 注意在合适的臂杆角度位置开始实验,避免导线缠绕 软件环境 ‐ LabVIEW 2012 ‐ ELVISmx ‐ Control Design and Simulation Module ‐ Quanser Engineering Trainer (QNET) module ‐ Acrobat Reader (pdf) 硬件环境 ‐ ELVIS‐II+ with power supply ‐ QNET ROTPENT with power supply ‐ PC platform with USB2.0 预备知识 ‐ LabVIEW 编程 ‐ 自动控制原理:动态系统建模与分析 ‐ 控制算法设计
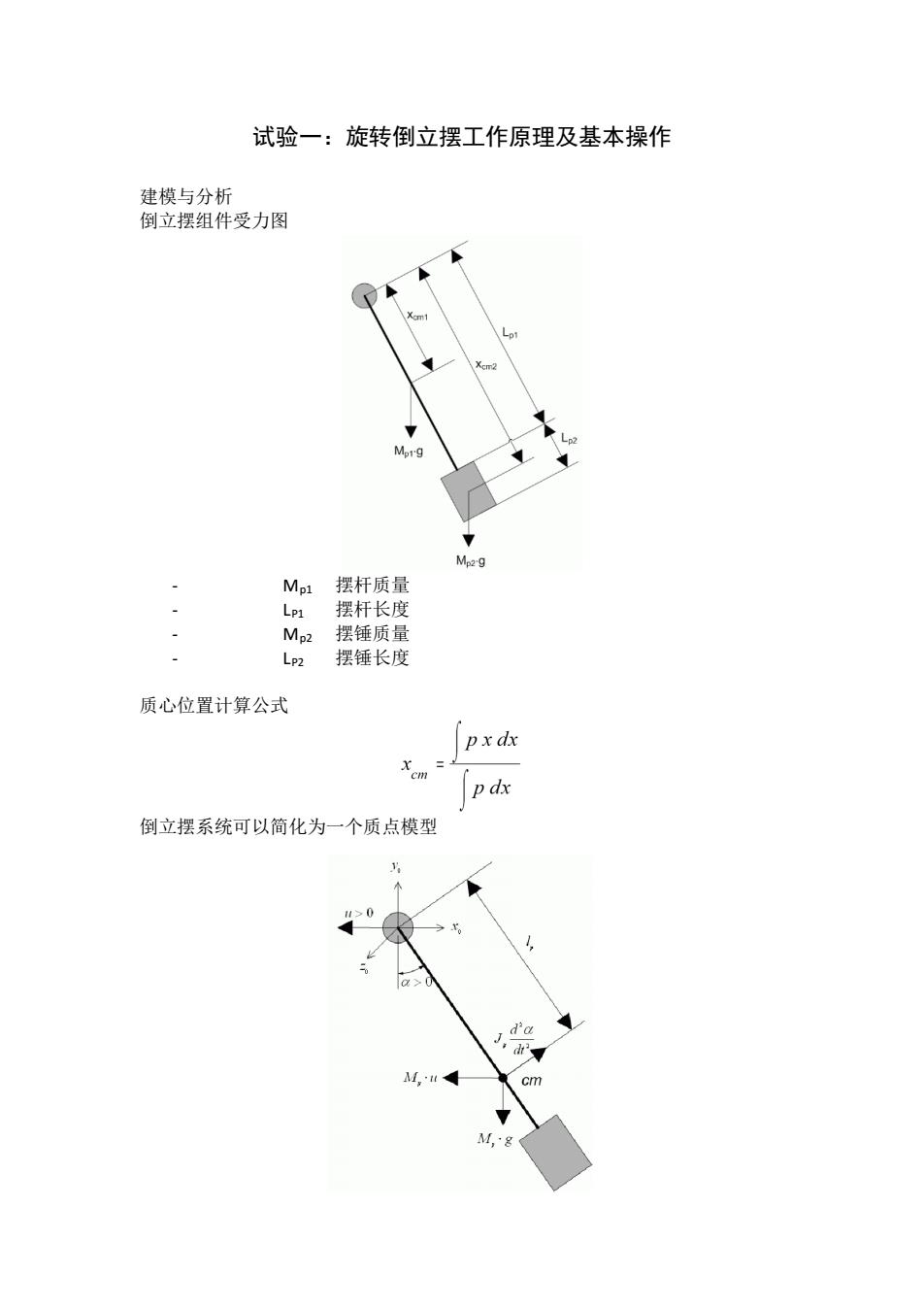
试验一:旋转倒立摆工作原理及基本操作 建模与分析 倒立摆组件受力图 Xcm2 -p2 Mprg Mp29 Mp1 摆杆质量 LP1 摆杆长度 Mp2 摆锤质量 Lp2 摆锤长度 质心位置计算公式 px dx p dx 倒立摆系统可以简化为一个质点模型 0 a>0 da J. M.u cm M,g
试验一:旋转倒立摆工作原理及基本操作 建模与分析 倒立摆组件受力图 ‐ Mp1 摆杆质量 ‐ LP1 摆杆长度 ‐ Mp2 摆锤质量 ‐ LP2 摆锤长度 质心位置计算公式 倒立摆系统可以简化为一个质点模型

质心位置计算公式 m:xcm.i i=1 cm m i=1 根据单质点受力图模型,得倒立摆非线性运动方程(EOM)如下: dp (t Mgl sin((t))+M ul cos(a (t)) D D D D Jp 倒立摆系统相对转轴Z0的转动惯量 Mp倒立摆组件的总重量 u 转轴的线加速度 倒立摆组件的质心位置 摆杆角度 从运动方程可以看出,当转轴向左加速时,惯性使得摆向上摇动(运动方程左边 项),而重力Mg和外力Mpu(运动方程右边项)则向下拉摆。 Jp可以通过实验方法进行估算,将运动方程在平衡位置附近进行线性化处理,通 过解算微分方程可得: JE D 4π2 f实验测量得出的摆动频率∫:,也可通过计算得出 J=r2dm Mp倒立摆组件的总重量 电机运转存在死区电压,需克服静摩擦阻力矩后才能运动。 物理概念分析 对比手动控制倒立摆的过程,要实现对倒立摆的自动控制,首先需要获得摆杆角 度信息,为了在一定的臂杆角度内实现控制,还需要知道臂杆的角度信息;要实 施平衡控制,还需要对电机进行适当的控制。本倒立摆系统为多输入(摆杆角度 α、角速度:臂杆角度日、角速度)、单输出(电机速度)系统。 对象状态反馈及控制接口,参考LabVIEW范例程序 (01-QNET_ROTPENT_Simple_Modeling.vi). 当偏角较小时,旋转倒立摆可采用一个简单的PD控制器进行平衡控制,控制算 法如下:
质心位置计算公式 根据单质点受力图模型,得倒立摆非线性运动方程(EOM)如下: ‐ Jp 倒立摆系统相对转轴 Z0的转动惯量 ‐ MP 倒立摆组件的总重量 ‐ u 转轴的线加速度 ‐ lP 倒立摆组件的质心位置 ‐ α 摆杆角度 从运动方程可以看出,当转轴向左加速时,惯性使得摆向上摇动(运动方程左边 项),而重力 Mpg 和外力 Mpu(运动方程右边项)则向下拉摆。 Jp 可以通过实验方法进行估算,将运动方程在平衡位置附近进行线性化处理,通 过解算微分方程可得: ‐ f 实验测量得出的摆动频率 ,也可通过计算得出 ‐ MP 倒立摆组件的总重量 电机运转存在死区电压,需克服静摩擦阻力矩后才能运动。 物理概念分析 对比手动控制倒立摆的过程,要实现对倒立摆的自动控制,首先需要获得摆杆角 度信息,为了在一定的臂杆角度内实现控制,还需要知道臂杆的角度信息;要实 施平衡控制,还需要对电机进行适当的控制。本倒立摆系统为多输入(摆杆角度 α、角速度;臂杆角度 θ、角速度)、单输出(电机速度)系统。 对象状态反馈及控制接口,参考 LabVIEW 范例程序 (01‐QNET_ROTPENT_Simple_Modeling.vi)。 当偏角较小时,旋转倒立摆可采用一个简单的 PD 控制器进行平衡控制,控制算 法如下: