西安电子科技大学：《现代测试导论》课程PPT教学课件（测量方法与测量理论）第二章 测试信号的时域分析与处理（南京理工大学）

南京理工大学机械工程学院精仪系 第2章 测试信号的时域分析与处理 2.1 信号时域特的获取方法 2.2k 信号数据插值方法及实现 2.3k 倍最数据的模方法及实现 2.4 教值微和数值分圾实现 2.5 肘戴信晋建方港及实现 2.6 MATLAB在时域分析与处理中的应用 2022-10-7 第2章测试信号的时域分析与处理

南京理工大学机械工程学院精仪系 2.1 信号时域特征的获取方法 2.2 信号与数据的插值方法及实现 2.3 信号与数据的拟合方法及实现 2.4 数值微分和数值积分及实现 2.5 时域信号的平滑与建模方法及实现 2.6 MATLAB在时域分析与处理中的应用

南京理工大学机械工程学院精仪系 信号时间特征 上升沿、下降沿：突变位置、时延 峰值：极值、上冲/下冲：二阶系统峰值比<----一-> 阻尼 拐点：特征点 过零点：脉冲反射计 峰高宽比、半高峰宽度：峰型 导函数、高阶导数：一阶、高阶频率分量 不动点、不变矩：克服背景变化、优化、特征提取、 上包络、下包络：信号最大值、背景波动 光滑性、增量表达：与函数导数有关（增量调制表达） 周期性：频率 波动性：纹波系数 短时平均幅度：（中值/均值滤波） 2022-10-7 第2章测试信号的时域分析与处理 2

南京理工大学机械工程学院精仪系 信号时间特征： 上升沿、下降沿：突变位置、时延 峰值：极值、上冲/下冲；二阶系统峰值比 <------> 阻尼 拐点：特征点 过零点：脉冲反射计 峰高宽比、半高峰宽度：峰型 导函数、高阶导数：一阶、高阶频率分量 不动点、不变矩：克服背景变化、优化、特征提取、 上包络、下包络：信号最大值、背景波动 光滑性、增量表达：与函数导数有关（增量调制表达） 周期性：频率 波动性：纹波系数 短时平均幅度：（中值/均值滤波）

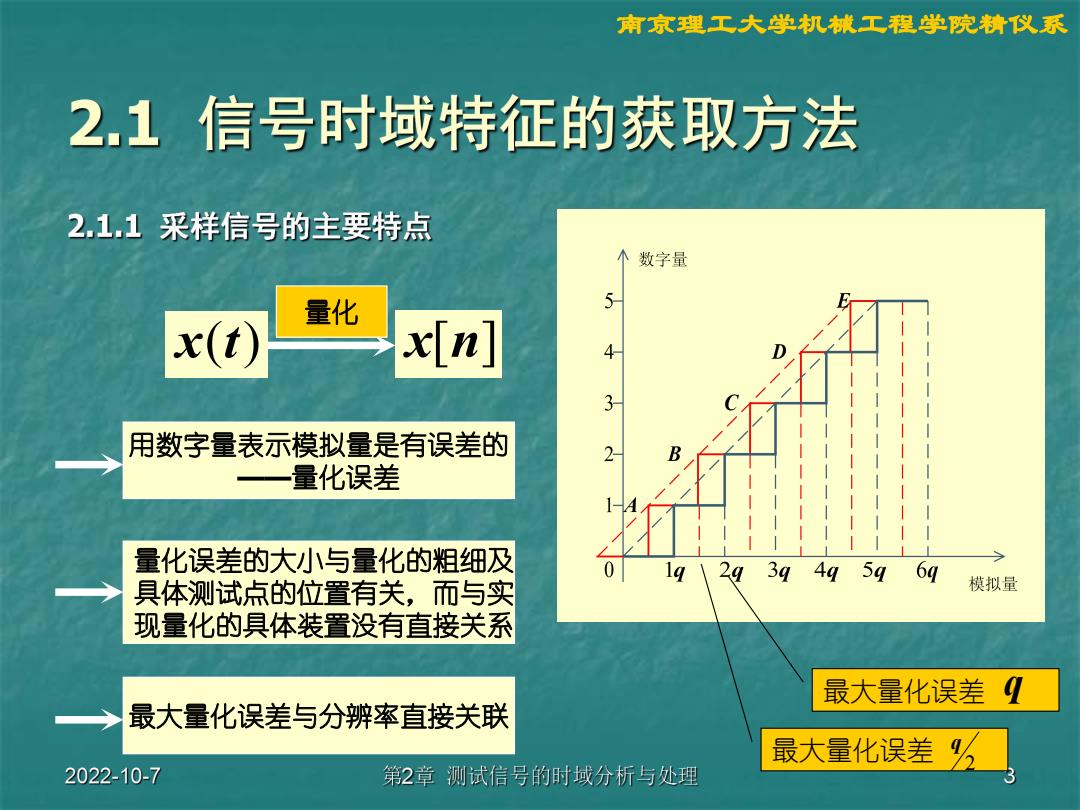
南京理工大学机械工程学院精仪系 2.1信号时域特征的获取方法 2.1.1采样信号的主要特点 个数字量 量化 5 x(t) x(n] 4 用数字量表示模拟量是有误差的 一一量化误差 量化误差的大小与量化的粗细及 1q\ 293949596q 具体测试点的位置有关，而与实 模拟量 现量化的具体装置没有直接关系 最大量化误差9 最大量化误差与分辨率直接关联 最大量化误差 2022-10-7 第2章测试信号的时域分析与处理

南京理工大学机械工程学院精仪系 x(t) 量化 用数字量表示模拟量是有误差的 ——量化误差 量化误差的大小与量化的粗细及 具体测试点的位置有关，而与实 现量化的具体装置没有直接关系 最大量化误差与分辨率直接关联 x[n] 最大量化误差 q 最大量化误差 2 q

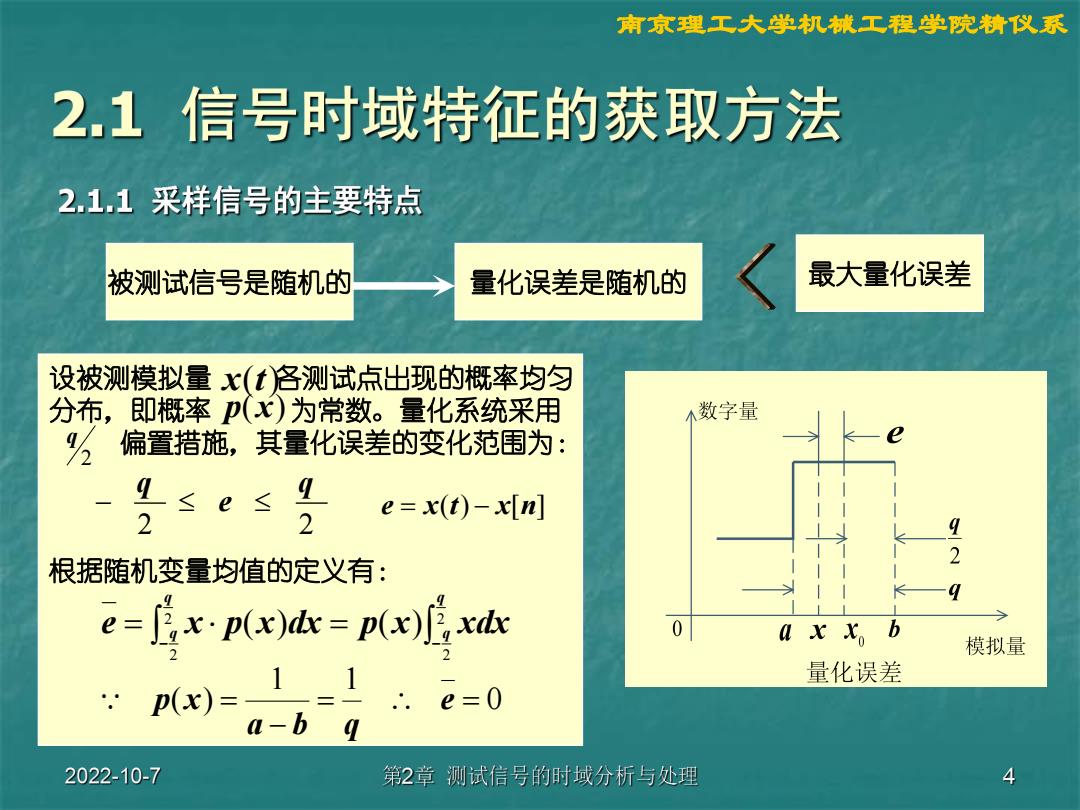
南京理工大学机械工程学院精仪系 2.1信号时域特征的获取方法 2.1.1采样信号的主要特点 被测试信号是随机的 量化误差是随机的 最大量化误差 设被测模拟量x(t各测试点出现的概率均匀 分布，即概率(x)为常数。量化系统采用 小数字量 偏置措施，其量化误差的变化范围为： ≤e ≤ e x(t)-x(n] 2 2 2 根据随机变量均值的定义有： e=道xpax)k=p(x)rd 0 axx。b 模拟量 量化误差 p(x)= 11 .e=0 a-b 2022-10-7 第2章测试信号的时域分析与处理 4

南京理工大学机械工程学院精仪系 被测试信号是随机的 量化误差是随机的 最大量化误差 设被测模拟量 各测试点出现的概率均匀 分布，即概率 为常数。量化系统采用 偏置措施，其量化误差的变化范围为： 根据随机变量均值的定义有： x(t) p x) 2 q 2 2 q e q    e  x(t)  x[n]        2 2 2 2 ( ) ( ) q q q e q x p x dx p x xdx 0 1 1 ( )      e a b q  p x

南京理工大学机械工程学院精仪系 2.1信号时域特征的获取方法 2.1.1采样信号的主要特点 :-(e-a).p(x)dep()de- e3/ → 13 12 0。= 23 以正弦 1「(2v-1)9 2 2 ·.SNR= 12 b=i01gn(3*-旷）=1ogw多+gn- 当N>1时，LR=(1.76+6.02N)dB 2022-10-7 第2章测试信号的时域分析与处理 5

南京理工大学机械工程学院精仪系 3 12 2 3 1 ( ) ( ) ( ) 2 2 2 3 2 2 2 2 2 2 2 e q q q e e p x de e p x de e q q q q q e  q                 以正弦信号为例计算该信号被采样和数字化而产生的信噪比SNR 2 2 ( ) 1 e b a x t dt b a SNR         N L N dB L q q SNR q dt T q t T E SNR N N SNR N N N T N x 1 (1.76 6.02 ) log 2 1 2 3 2 1 10 log 2 3 10 log (2 1) 2 3 12 2 (2 1) 2 1 2 (2 1) 2 1 sin (2 ) 2 1 (2 1) 2 10 10 2 10 2 2 2 2 2 2 0                                                     当 时， 