上海交通大学：《现代控制理论基础》课程教学资源（课件讲稿）第一章 线性系统的数学描述

第一章 线性系统的数学描述

第一章 线性系统的数学描述

1.1引言 1、建立系统的数学模型是控制系统进行分析和设 计的基础 系统的数学模型— 描述系统行为特性的数学 表达式（如传递函数）或数学方程（如微分方程、代 数方程) 2、同一个系统可以有不同的数学模型 ·系统研究的对象（输入、输出和状态变量）不同 。建立数学模型所用的数学方法不同 3、举例：直流电动机控制电路的数学模型

1.1 引 言 1、建立系统的数学模型是控制系统进行分析和设 计的基础 系统的数学模型——描述系统行为特性的数学 表达式(如传递函数)或数学方程(如微分方程、代 数方程) 2、同一个系统可以有不同的数学模型 系统研究的对象(输入、输出和状态变量）不同 建立数学模型所用的数学方法不同   3、举例：直流电动机控制电路的数学模型

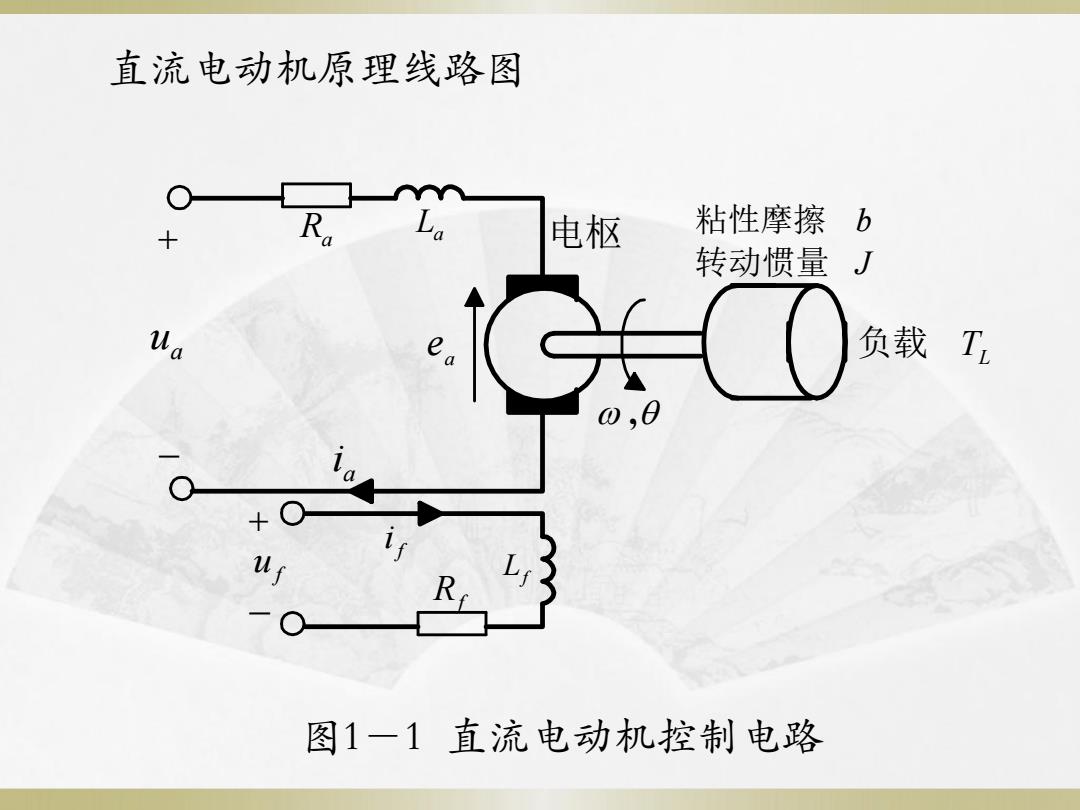
直流电动机原理线路图 粘性摩擦b + R 电枢 转动惯量J 负载 T uf 图1一1直流电动机控制电路

u f ua f i a i Ra Rf Lf La      , 转动惯量 J 粘性摩擦 b 负载 TL 电枢 a e 直流电动机原理线路图 图1－1 直流电动机控制电路

(1)电枢控制方式：设激磁电压、气隙磁通恒定 ·电枢电路电压平衡方程 u。=Rin+L di。+e。 dt (1-3) 式中，R。La分别是电枢电路的电阻和电感 电机的反电势与电机的角速度成正比： e。=K.o (1-2) 式中，K。为电机的反电势常数 ·电机转子轴上转矩平衡方程 T=J do+b+T (1-4) d

⑴电枢控制方式：设激磁电压、气隙磁通恒定 电枢电路电压平衡方程 式中， 分别是电枢电路的电阻和电感 电机的反电势与电机的角速度成正比： 式中， 为电机的反电势常数 电机转子轴上转矩平衡方程   （1－3） （1－4） （1－2） a a a a a a e dt di u  R i  L  e a  K e  Ra、La i T L b dt d T  J     K e 

式中 J为电机轴上总的等效转动惯量， b 为电机转轴上的等效粘性摩擦系数， T是负载转矩 T,是电动机电磁转矩 T:=Kiia (1-1) ●以电压u。为输入，角速度⊙为输出的运动方程 在以上各式中，消去中间变量。，并假定T,=0 得如下二阶微分方程 +(R.al*b)+(k.ki+Rbo-k

式中 为电机轴上总的等效转动惯量， 为电机转轴上的等效粘性摩擦系数， 是负载转矩 以电压 为输入，角速度 为输出的运动方程 在以上各式中，消去中间变量 ，并假定 得如下二阶微分方程 是电动机电磁转矩  （1－1） （1－5） J b TL Ti a u  a TL  0 i a a a KeKt Rab Ktua dt d R J bL dt d L J         ( ) ( ) 2 2  Ti Ki a  i