
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 第五章系统稳定性 5.1稳定性的经典定义 实际系统正常工作的前提是系统必须是稳定的 系统稳定性有几种不同的定义 稳定性经典定义:对系统闭环传递函数定义的稳定性,是有 界输入有界输出稳定性(BIBO稳定性) 定义5.1.1老虑线性系统,如果由有界给定值输入所产生 的系统输出也是有界的,则称系统是BIB0稳定的
第五章 系统稳定性 5.1 稳定性的经典定义 实际系统正常工作的前提是系统必须是稳定的 系统稳定性有几种不同的定义 稳定性经典定义:对系统闭环传递函数定义的稳定性,是有 界输入有界输出稳定性(BIBO稳定性 ) 定义5.1.1 考虑线性系统,如果由有界给定值输入所产生 的系统输出也是有界的, 则称系统是BIBO稳定的

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 定理5.1.1单变量线性系统的BIB0稳定的充分必要条件是 所有闭环极点都具有负实部 例5.1.1设闭环系统的状态空间描述为 -10 1 x- x+ 0 2.5 0 y=[1 1] 其传递函数为 8(s)=c(SI-A)b= (s-2.5)1 (s+1)(s-2.5)(s+1) 所以系统是BIB0稳定的
定理5.1.1 单变量线性系统的BIBO稳定的充分必要条件是 所有闭环极点都具有负实部 例5.1.1 设闭环系统的状态空间描述为 [ ] x x x 1 1 0 1 0 2.5 1 0 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ + ⎦ ⎤ ⎢ ⎣ ⎡ − = y & u 其传递函数为 ( 1 ) 1 ( 1)( 2.5 ) ( 2.5 ) ( ) ( ) 1 + = + − − = − = − s s s s g s c sI A b 所以系统是BIBO稳定的

上濟究通大学 SHANGHAI JIAO TONG UNIVERSITY 5.2内部稳定性 稳定性一输出稳定,也就是当系统在干扰取消后,在一定时 间内,其输出会恢复到原来的稳态输出 内部稳定性一针对系统内部状态,反映的是系统内部状态受 干扰信号的影响。当扰动信号取消后,系统的内部状态会在 一定时间内恢复到原来的平衡状态,则称系统内稳定 定义5.2.1考虑线性系统,如果在系统任何一点有界输入 在其他点所产生的输出都是有界的,则称系统是内稳定的
5.2 内部稳定性 稳定性-输出稳定,也就是当系统在干扰取消后,在一定时 间内,其输出会恢复到原来的稳态输出 定义5.2.1 考虑线性系统,如果在系统任何一点有界输入 在其他点所产生的输出都是有界的,则称系统是内稳定的 内部稳定性-针对系统内部状态,反映的是系统内部状态受 干扰信号的影响。当扰动信号取消后,系统的内部状态会在 一定时间内恢复到原来的平衡状态,则称系统内稳定
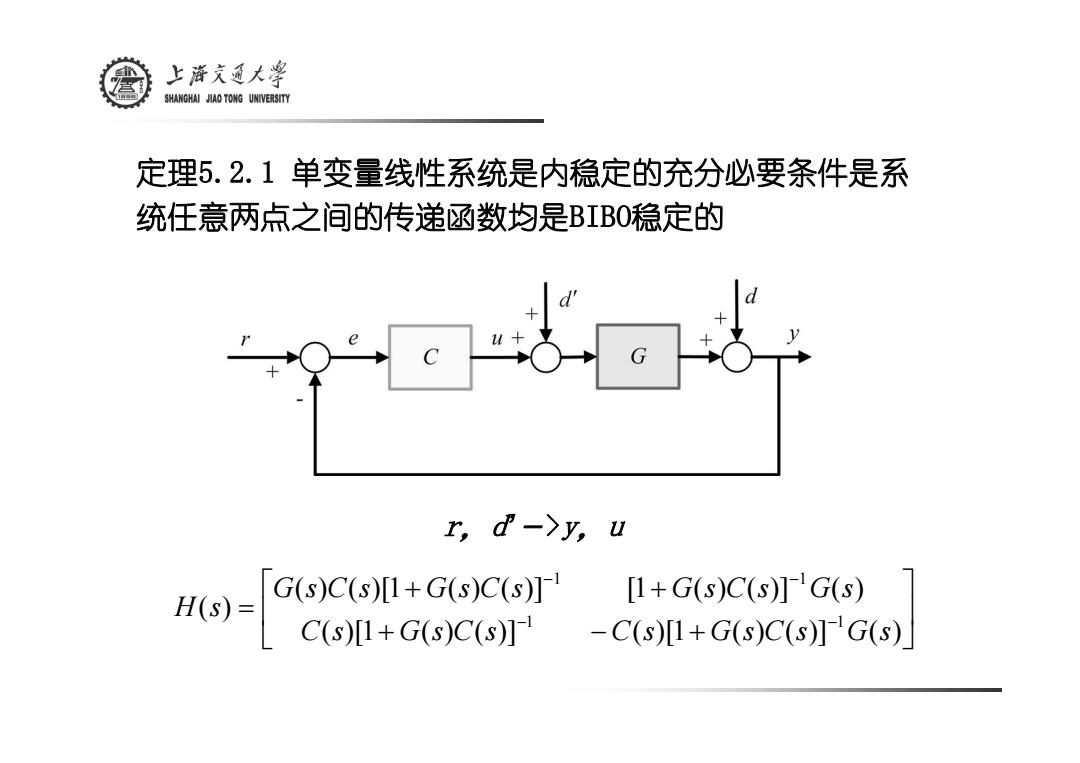
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 定理5.2.1单变量线性系统是内稳定的充分必要条件是系 统任意两点之间的传递函数均是BIBO稳定的 r,d->y,u H(S)= G(s)C(s)[1+G(s)C(s)]1 [1+G(s)C(s)]G(s) C(s)[I+G(s)C(s)】 -C(s)1+G(s)C(s)1G(s)
定理5.2.1 单变量线性系统是内稳定的充分必要条件是系 统任意两点之间的传递函数均是BIBO稳定的 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − + + + = − − − − ( )[ 1 ( ) ( )] ( )[ 1 ( ) ( )] ( ) ( ) ( )[ 1 ( ) ( )] [ 1 ( ) ( )] ( ) ( ) 1 1 1 1 C s G s C s C s G s C s G s G s C s G s C s G s C s G s H s r,d’ - >y,u
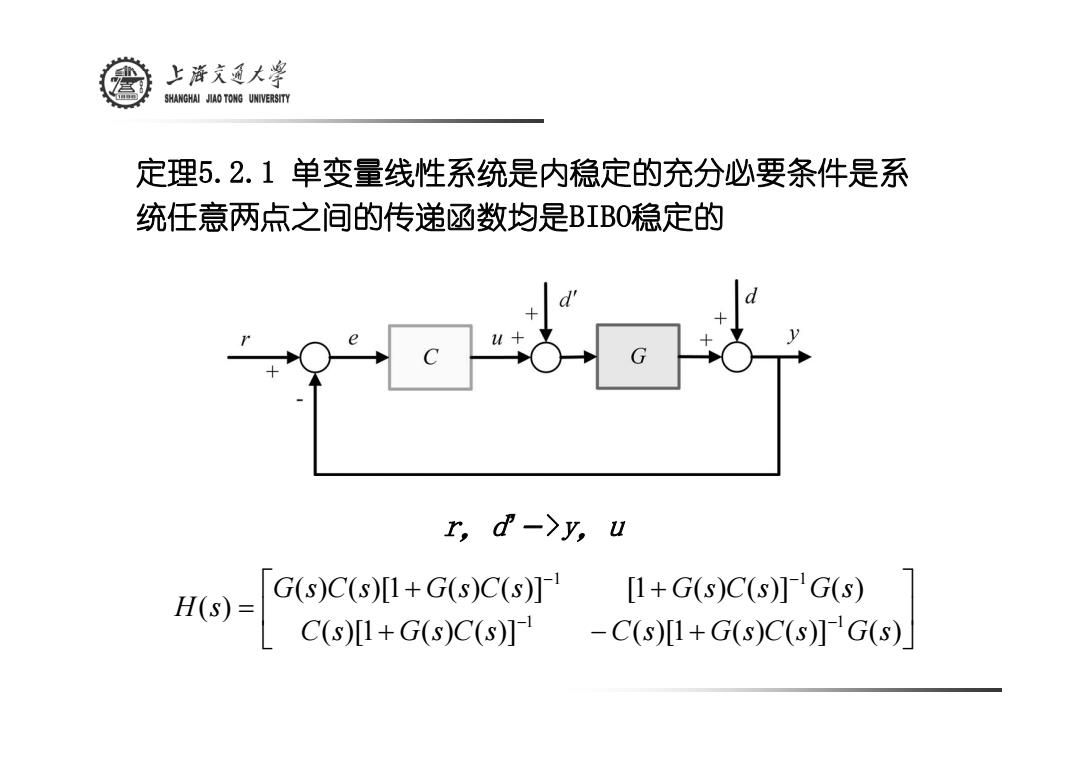
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 定理5.2.1单变量线性系统是内稳定的充分必要条件是系 统任意两点之间的传递函数均是BIBO稳定的 r,d->y,u H(S)= G(s)C(s)[1+G(s)C(s)]1 [1+G(s)C(s)]G(s) C(s)[I+G(s)C(s)】 -C(s)1+G(s)C(s)1G(s)
定理5.2.1 单变量线性系统是内稳定的充分必要条件是系 统任意两点之间的传递函数均是BIBO稳定的 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − + + + = − − − − ( )[ 1 ( ) ( )] ( )[ 1 ( ) ( )] ( ) ( ) ( )[ 1 ( ) ( )] [ 1 ( ) ( )] ( ) ( ) 1 1 1 1 C s G s C s C s G s C s G s G s C s G s C s G s C s G s H s r,d’ - >y,u