《线性代数》课程教学课件（讲稿，B）第三章 矩阵的运算 §3.2 逆矩阵

第三章矩阵的运算 二、矩阵可逆的条件 设 41 12 A= 22 n An (n2 我们构造矩阵 A2 。 A n2 称为A的伴随矩阵 : 2 nn

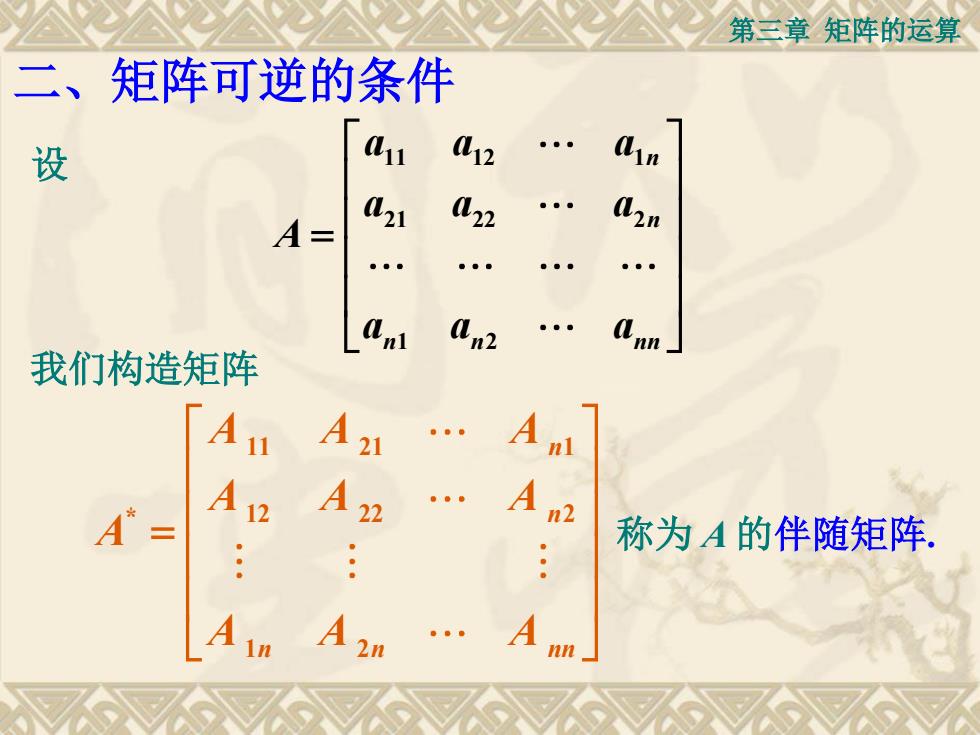
第三章 矩阵的运算 我们构造矩阵 11 21 1 * 12 22 2 1 2 n n n n nn A A A A A A A A A A       =       称为 A 的伴随矩阵. 设 11 12 1 21 22 2 1 2 n n n n nn a a a a a a A a a a       =       二、矩阵可逆的条件

第三章矩阵的运算 A2 A A"= A22 .An2 A2n nn 伴随矩阵在位置(i,)上的元素是矩阵A在位置(，)上的代 数余子式 伴随矩阵为什么这样定义？是因为AA或AA会得 到一个非常漂亮的结果

第三章 矩阵的运算 伴随矩阵为什么这样定义? 是因为 或 会得 到⼀个⾮常漂亮的结果. * AA * A A 11 21 1 * 12 22 2 1 2 n n n n nn A A A A A A A A A A       =       伴随矩阵 在位置 上的元素是矩阵 A 在位置 上的代 数余子式 * A (i j , ) ( j i, )

第三章矩阵的运算 由于 an+a:4++0n4n=1i=j 0i≠j 44+4-

第三章 矩阵的运算 1 1 2 2 1 1 2 2 0 0 i j i j in jn i j i j ni nj A i j a A a A a A i j A i j a A a A a A i j  = + + + =    = + + + =   由于

第三章矩阵的运算 可得： 12 A A21 nl A4" 21 22 。 @2n A22 A n2 2 A in A nn 0 0 0 0 -AE A"A 0 0 . 只要1≠0，就有4()=（同4A=E

第三章 矩阵的运算 可得： | | 0 0 0 | | 0 0 0 | | A A A E A     = =   1 1 * * A A A A A E 0 ( ) ( ) A A 只 要  = = ，就有 21 1 21 11 12 1 11 121 22 2 222 * 2 1 2 nn n n nn n nn nn n a a a A A a a a AA AA AA A a a A a A         =     A A =