》兆性蝶日 品 回 器一 第四步:点击“解决按钮,得出计算结果。本题的运行结果界面如下 念结果给出 石回区 相差值 当前值 上限 颜项而 限 下限 上限 2 器 第五步:分析运行结果。 本题中目标函数的最优值是27500,x1=50,x2=250
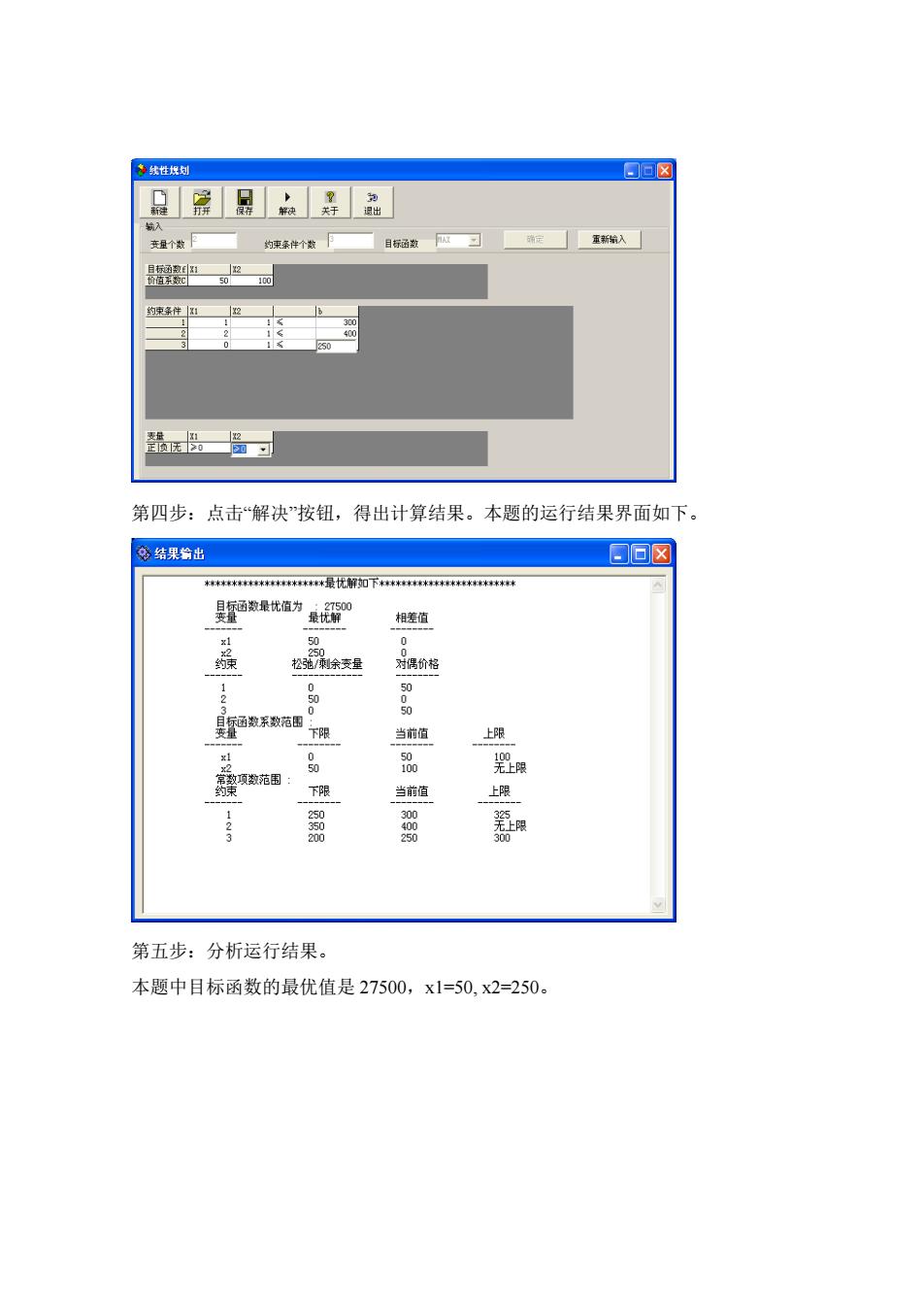
第四步:点击“解决”按钮,得出计算结果。本题的运行结果界面如下。 第五步:分析运行结果。 本题中目标函数的最优值是 27500,x1=50, x2=250

§4人力资源分配的问题 例1.某昼夜服务的公交线路每天各时间段内所需司机 和乘务人员数如下: 班次 时间 所需人数 1 6:00-—10:00 60 10:00 14:00 70 14:00 -18:00 60 418:00 -22:00 50 22:00-2:00 20 62:00-6:00 30 设司机和乘务人员分别在各时间段一开始时上班,并 连续工作八小时,问该公交线路怎样安排司机和乘务人员, 既能满足工作需要,又配备最少司机和乘务人员? 解:设x表示第i班次时开始上班的司机和乘务人员数 这样我们建立如下的数学模型。 目标函数:Mimx1+x2+x3+x4+x5+x6 约束条件:s.t.x1+x6≥60 x1+x2≥70 x2+x3≥60 x3+x4≥50 x4+x5≥20 x5+x6≥30 x1,x2,x3,x4,x5,x6≥0 例2.一家中型的百货商场,它对售货员的需求经过统计分析如下表所示。为了保 证售货人员充分休息,售货人员每周工作5天,休息两天,并要求休息的两天是 连续的。问应该如何安排售货人员的作息,既满足工作需要,又使配备的售货人 员的人数最少?
§4 人力资源分配的问题 例 1.某昼夜服务的公交线路每天各时间段内所需司机 和乘务人员数如下: 设司机和乘务人员分别在各时间段一开始时上班,并 连续工作八小时,问该公交线路怎样安排司机和乘务人员, 既能满足工作需要,又配备最少司机和乘务人员? 解:设 xi 表示第 i 班次时开始上班的司机和乘务人员数, 这样我们建立如下的数学模型。 目标函数: Min x1 + x2 + x3 + x4 + x5 + x6 约束条件:s.t. x1 + x6 ≥ 60 x1 + x2 ≥ 70 x2 + x3 ≥ 60 x3 + x4 ≥ 50 x4 + x5 ≥ 20 x5 + x6 ≥ 30 x1,x2,x3,x4,x5,x6 ≥ 0 例 2.一家中型的百货商场,它对售货员的需求经过统计分析如下表所示。为了保 证售货人员充分休息,售货人员每周工作 5 天,休息两天,并要求休息的两天是 连续的。问应该如何安排售货人员的作息,既满足工作需要,又使配备的售货人 员的人数最少? 班次 时间 所需人数 1 6:00 —— 10:00 60 2 10:00 —— 14:00 70 3 14:00 —— 18:00 60 4 18:00 —— 22:00 50 5 22:00 —— 2:00 20 6 2:00 —— 6:00 30
时间 所需售货员人数 星期▣ 星期■ 星期三 24 昆期三 )5 星期四 19 星期五 31 星期六 28 解:设x(i=1,2,7)表示星期一至日开始休息的人数,建立如下的数学模型 目标函数:Minx1+X2+x3+x4+x5+x6+x7 约束条件:st.x1+x2+x3+x4+x5≥28 x2+x3+x4+x5+x6≥15 x3+x4+x5+x6+x7≥24 x4+x5+x6+x7+x1≥25 x5+x6+x7+x1+x2≥19 x6+x7+x1+x2+x3≥31 x7+x1+x2+x3+x4≥28 xl.x2.x3.x4.x5.x6.x7>0 §5生产计划的问题 例3.某公司面临一个是外包协作还是自行生产的问题。该公司生产甲、乙、丙三 种产品,都需要经过铸造、机加工和装配三个车间。甲、乙两种产品的铸件可以 外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量。数据如表。 问:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产 品的铸造中,由本公司铸造和由外包协作各应多少件? 甲乙丙资源限制■ 铸造工时(小时/件) 5 10 8000 机加工工时(小时/件)6 4 Q 12000 装配工时(小时件) 10000 自产铸件成本(元/件)3 5 4 外协铸件成本(元/件) 机加工成本(元/件) 2 3 装配成本(元/件) 2 产品售价(元/件)231816
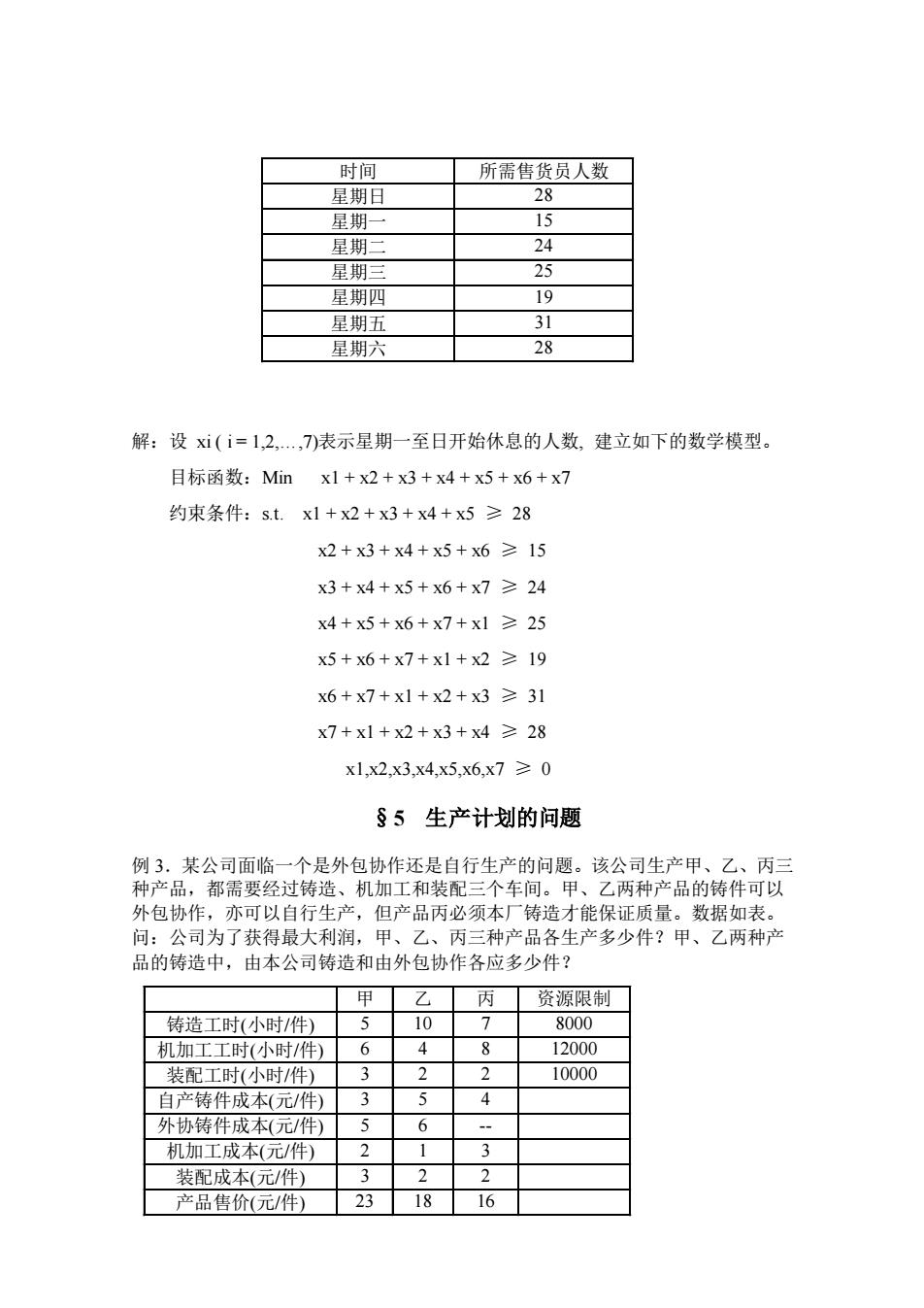
时间 所需售货员人数 星期日 28 星期一 15 星期二 24 星期三 25 星期四 19 星期五 31 星期六 28 解:设 xi ( i = 1,2,.,7)表示星期一至日开始休息的人数, 建立如下的数学模型。 目标函数:Min x1 + x2 + x3 + x4 + x5 + x6 + x7 约束条件:s.t. x1 + x2 + x3 + x4 + x5 ≥ 28 x2 + x3 + x4 + x5 + x6 ≥ 15 x3 + x4 + x5 + x6 + x7 ≥ 24 x4 + x5 + x6 + x7 + x1 ≥ 25 x5 + x6 + x7 + x1 + x2 ≥ 19 x6 + x7 + x1 + x2 + x3 ≥ 31 x7 + x1 + x2 + x3 + x4 ≥ 28 x1,x2,x3,x4,x5,x6,x7 ≥ 0 §5 生产计划的问题 例 3.某公司面临一个是外包协作还是自行生产的问题。该公司生产甲、乙、丙三 种产品,都需要经过铸造、机加工和装配三个车间。甲、乙两种产品的铸件可以 外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量。数据如表。 问:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产 品的铸造中,由本公司铸造和由外包协作各应多少件? 甲 乙 丙 资源限制 铸造工时(小时/件) 5 10 7 8000 机加工工时(小时/件) 6 4 8 12000 装配工时(小时/件) 3 2 2 10000 自产铸件成本(元/件) 3 5 4 外协铸件成本(元/件) 5 6 - 机加工成本(元/件) 2 1 3 装配成本(元/件) 3 2 2 产品售价(元/件) 23 18 16

解:设x1,x2,x3分别为三道工序都由本公司加工的甲、乙、丙三种产品的件数 x4,x5分别为由外协铸造再由本公司加工和装配的甲、乙两种产品的件数。 求x的利润:利润=售价·各成本之和 产品甲全部自制的利润 =23-(3+2+3片15 产品甲铸造外协,其余自制的利润 =23-(5+2+3F13 产品乙全部自制的利润 =18-(5+1+2=10 产品乙铸造外协,其余自制的利润 =18-(6+1+2=9 产品丙的利润 =16-(4+3+27 可得到x(i=1,2,3,4,5)的利润分别为15、10、7、13、9元。 通过以上分析,可建立如下的数学模型: 目标函数:Max15x1+10x2+7x3+13x4+9x5 约束条件: 5x1+10x2+7x3≤8000 6x1+4x2+8x3+6x4+4x5≤12000 3x1+2x2+2x3+3x4+2x5≤10000 x1,x2,x3,x4,x5≥0 例4.永久机械厂生产【、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。设有 两种规格的设备A1、A2能完成A工序:有三种规格的设备B1、B2、B3能完成 B工序。I可在A、B的任何规格的设备上加工:Ⅱ可在任意规格的A设备上加 工,但对B工序,只能在B1设备上加工:Ⅲ只能在A2与B2设备上加工。数据 如表。问:为使该厂获得最大利润,应如何制定产品加工方案? 产品单件工时 设备的满负荷时的 设备 有效台时 设备费用 A1 6000 0 12 B 73 4000 20 原料(元/件)0.2 035 0.50 售价(元/件)1.252.002.80 解:设x表示第i种产品,在第j种工序上的第k种设备上加工的数量。建 立如下的数学模型: s.t.5x111+10x211 ≤6000 (设备A1) 7x112+9x212+12x312≤10000 (设备A2)
解:设 x1,x2,x3 分别为三道工序都由本公司加工的甲、乙、丙三种产品的件数, x4,x5 分别为由外协铸造再由本公司加工和装配的甲、乙两种产品的件数。 求 xi 的利润:利润 = 售价 - 各成本之和 产品甲全部自制的利润 =23-(3+2+3)=15 产品甲铸造外协,其余自制的利润 =23-(5+2+3)=13 产品乙全部自制的利润 =18-(5+1+2)=10 产品乙铸造外协,其余自制的利润 =18-(6+1+2)=9 产品丙的利润 =16-(4+3+2)=7 可得到 xi(i = 1,2,3,4,5) 的利润分别为 15、10、7、13、9 元。 通过以上分析,可建立如下的数学模型: 目标函数: Max 15x1 + 10x2 + 7x3 + 13x4 + 9x5 约束条件: 5x1 + 10x2 + 7x3 ≤ 8000 6x1 + 4x2 + 8x3 + 6x4 + 4x5 ≤ 12000 3x1 + 2x2 + 2x3 + 3x4 + 2x5 ≤ 10000 x1,x2,x3,x4,x5 ≥ 0 例 4.永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过 A、B 两道工序加工。设有 两种规格的设备 A1、A2 能完成 A 工序;有三种规格的设备 B1、B2、B3 能完成 B 工序。Ⅰ可在 A、B 的任何规格的设备上加工;Ⅱ 可在任意规格的 A 设备上加 工,但对 B 工序,只能在 B1 设备上加工;Ⅲ只能在 A2 与 B2 设备上加工。数据 如表。问:为使该厂获得最大利润,应如何制定产品加工方案? 解:设 xijk 表示第 i 种产品,在第 j 种工序上的第 k 种设备上加工的数量。建 立如下的数学模型: s.t. 5x111 + 10x211 ≤ 6000 ( 设备 A1 ) 7x112 + 9x212 + 12x312 ≤ 10000 ( 设备 A2 ) 产品单件工时 设备 Ⅰ Ⅱ Ⅲ 设备的 有效台时 满负荷时的 设备费用 A1 5 10 6000 300 A2 7 9 12 10000 321 B1 6 8 4000 250 B2 4 11 7000 783 B3 7 4000 200 原料(元/件) 0.25 0.35 0.50 售价(元/件) 1.25 2.00 2.80

6x121+8x221 ≤4000 (设备B1) 4x122 +11x322≤7000 (设备B2) 7x123 ≤4000 (设备B3) x111+x112-x121-x122-x123=0 (I产品在A、B工序加工的数量相等) x211+x212-X221 =0 (Ⅱ产品在A、B工序加工的数量相等) x312 x322 =0 (Ⅲ产品在A、B工序加工的数量相等) xk≥0,i=1,2,3:j=1,2k=1,2,3 目标函数为计算利润最大化,利润的计算公式为: 利润=[(销售单价·原料单价)幸产品件数]之和·(每台时的设备费用*设 备实际使用的总台时数)之和。 这样得到目标函数: Max(1.25-0.25)x111+x112H(2-0.35)x221+(2.80-0.5x312 300/6000(5xI11+10x211)321/10000(7x112+9x212+12x312) 250/4000(6x121+8x221783/7000(4x122+11x322200/4000(7x123) 经整理可得: Max0.75x111+0.7753x112+1.15x211+1.3611x212+1.9148x312 0.375x121-0.5x221-0.4475x122-1.2304x322-0.35x123 §6套裁下料问题 例5.某工厂要做100套钢架,每套用长为2.9m,2.1m,1.5m的圆钢各一根。己知 原料每根长7.4m,问:应如何下料,可使所用原料最省? 解:共可设计下列5种下料方案,见下表 方案1 方案2方案3方案4方案5 29m 2 0 0 21m 15m 利余料头 0.1 02 0.3 0.8
6x121 + 8x221 ≤ 4000 ( 设备 B1 ) 4x122 + 11x322 ≤ 7000 ( 设备 B2 ) 7x123 ≤ 4000 ( 设备 B3 ) x111+ x112- x121- x122- x123 = 0 (Ⅰ产品在 A、B 工序加工的数量相等) x211+ x212- x221 = 0 (Ⅱ产品在 A、B 工序加工的数量相等) x312 - x322 = 0 (Ⅲ产品在 A、B 工序加工的数量相等) xijk ≥ 0 , i = 1,2,3; j = 1,2; k = 1,2,3 目标函数为计算利润最大化,利润的计算公式为: 利润 = [(销售单价 - 原料单价)* 产品件数]之和 -(每台时的设备费用*设 备实际使用的总台时数)之和。 这样得到目标函数: Max (1.25-0.25)(x111+x112)+(2-0.35)x221+(2.80-0.5)x312 – 300/6000(5x111+10x211)-321/10000(7x112+9x212+12x312)- 250/4000(6x121+8x221)-783/7000(4x122+11x322)-200/4000(7x123). 经整理可得: Max 0.75x111+0.7753x112+1.15x211+1.3611x212+1.9148x312- 0.375x121-0.5x221-0.4475x122-1.2304x322-0.35x123 §6 套裁下料问题 例 5.某工厂要做 100 套钢架,每套用长为 2.9 m,2.1 m,1.5 m 的圆钢各一根。已知 原料每根长 7.4 m,问:应如何下料,可使所用原料最省? 解: 共可设计下列 5 种下料方案,见下表 方案 1 方案 2 方案 3 方案 4 方案 5 2.9 m 1 2 0 1 0 2.1 m 0 0 2 2 1 1.5 m 3 1 2 0 3 合计 7.4 7.3 7.2 7.1 6.6 剩余料头 0 0.1 0.2 0.3 0.8