
第三章 运输问题 ● §1 运输模型 ● §2 运输问题的计算机求解 §3 运输问题的应用
管 理 运 筹 学 1 第三章 运 输 问 题 • §1 运 输 模 型 • §2 运输问题的计算机求解 • §3 运输问题的应用
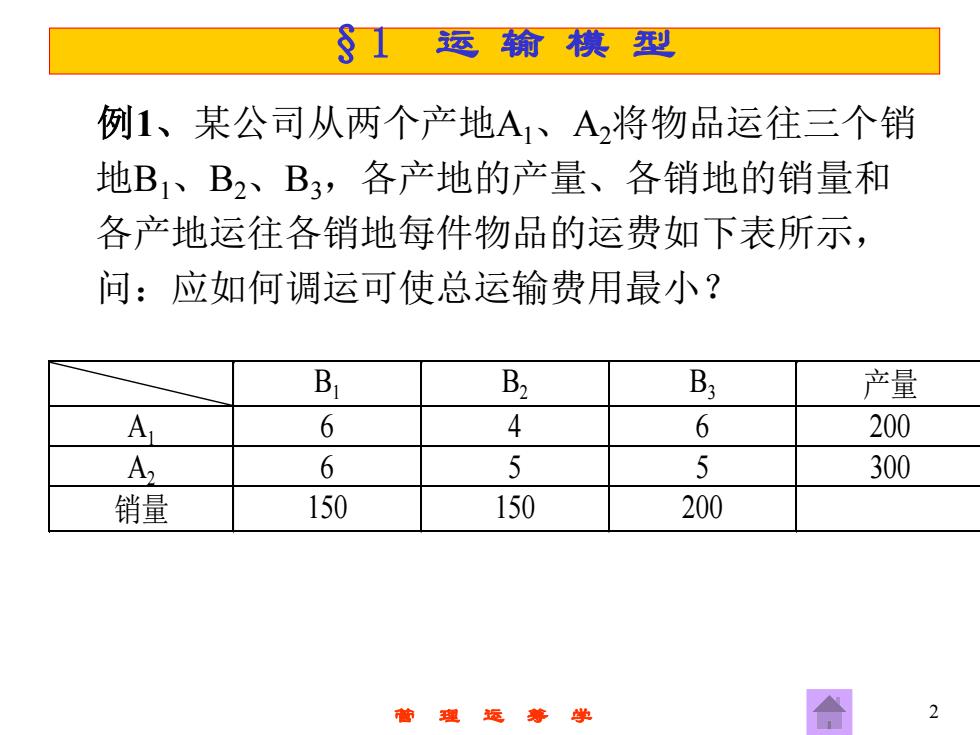
§1运输模型 例1、某公司从两个产地A、A将物品运往三个销 地B1、B2、B3,各产地的产量、各销地的销量和 各产地运往各销地每件物品的运费如下表所示, 问:应如何调运可使总运输费用最小? B B2 B 产量 A 6 4 6 200 A 6 5 5 300 销量 150 150 200 2
管 理 运 筹 学 2 例1、某公司从两个产地A1、A2将物品运往三个销 地B1、B2、B3,各产地的产量、各销地的销量和 各产地运往各销地每件物品的运费如下表所示, 问:应如何调运可使总运输费用最小? B1 B2 B3 产量 A1 6 4 6 200 A2 6 5 5 300 销量 150 150 200 §1 运 输 模 型
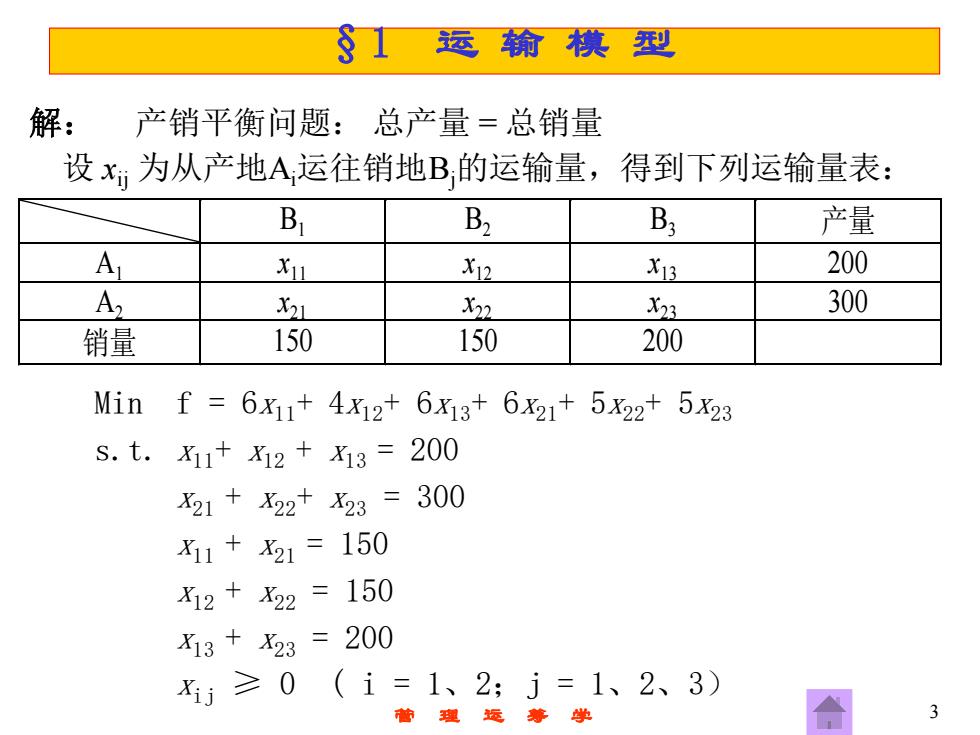
S1运输模型 解: 产销平衡问题:总产量=总销量 设x:为从产地A运往销地B的运输量,得到下列运输量表: B B2 B 产量 A Xu X12 X13 200 A X21 X22 X23 300 销量 150 150 200 Min i f=6X11+4x12+6x13+6x21+522+5x23 S.t.X1+为12+为13= 200 21+X22+X23= 300 1+21=150 X12+22=150 X13+X23= 200 X)≥0 (i=1、2;j=1、2、3) 理运筹学
管 理 运 筹 学 3 解: 产销平衡问题: 总产量 = 总销量 设 xij 为从产地Ai运往销地Bj的运输量,得到下列运输量表: B1 B2 B3 产量 A1 x11 x12 x13 200 A2 x21 x22 x23 300 销量 150 150 200 Min f = 6x11+ 4x12+ 6x13+ 6x21+ 5x22+ 5x23 s.t. x11+ x12 + x13 = 200 x21 + x22+ x23 = 300 x11 + x21 = 150 x12 + x22 = 150 x13 + x23 = 200 xij ≥ 0 ( i = 1、2;j = 1、2、3) §1 运 输 模 型

§1 运输模型 一般运输模型:产销平衡 A1、A2、.、 Am表示某物资的m个产地;B1、 B2、Bn表示某物质的n个销地;g表示产地A的产量; d表示销地B的销量;c表示把物资从产地A运往销地B 的单位运价。 设x:为从产地A运往销地B,的运输量,得到下列一般运输 量问题的模型: Min f=∑∑CX i=1j=1 S.t. ∑x对=Si=1,2,.,m Σ=4j=1,2.n x≥0(i=1,2,.m;j=1,2,.n) 曹理运筹学 4
管 理 运 筹 学 4 §1 运 输 模 型 • 一般运输模型:产销平衡 A1、 A2、.、 Am 表示某物资的m个产地; B1、 B2、.、Bn 表示某物质的n个销地;si 表示产地Ai的产量; dj 表示销地Bj 的销量; cij 表示把物资从产地Ai运往销地Bj 的单位运价。 • 设 xij 为从产地Ai运往销地Bj的运输量,得到下列一般运输 量问题的模型: m n Min f = cij xij i = 1 j = 1 n s.t. xij = si i = 1,2,.,m j = 1 m xij = dj j = 1,2,.,n i = 1 xij ≥ 0 (i = 1,2,.,m ; j = 1,2,.,n)

§1运输模型 变化: 1)有时日标函数求最大。如求利润最大或营业额 最大等; 2)当某些运输线路上的能力有限制时,在模型中 直接加入约束条件(等式或不等式约束); 3)产销不平衡时,可加入假想的产地(销大于产 时)或销地(产大于销时)。 5
管 理 运 筹 学 5 §1 运 输 模 型 • 变化: 1)有时目标函数求最大。如求利润最大或营业额 最大等; 2)当某些运输线路上的能力有限制时,在模型中 直接加入约束条件(等式或不等式约束); 3)产销不平衡时,可加入假想的产地(销大于产 时)或销地(产大于销时)