
Max z=50x1+100x2 约束条件: s.t.xI+ x2≤300(A) 2x1+ x2≤400 (B) x2≤250 c xl≥0(D) 2 ≥0(E) 得到最优解:xl=50, x2=250 最优目标值z=27500 (1)分别取决策变量X1,X2为坐标向量建立直角坐标系。在直角坐标系里,图上 任意一点的坐标代表了决策变量的一组值,例1的每个约束条件都代表一个半平 面。 X,≥0 X1≥0 X1=0 X2=0 (2)对每个不等式(约束条件),先取其等式在坐标系中作直线,然后确定不等式 所决定的半平面
Max z = 50 x1 + 100 x2 约束条件: s.t. x1 + x2 ≤ 300 (A) 2 x1 + x2 ≤ 400 (B) x2 ≤ 250 (C) x1 ≥ 0 (D) x2 ≥ 0 (E) 得到最优解: x1 = 50, x2 = 250 最优目标值 z = 27500 (1)分别取决策变量 X1 , X2 为坐标向量建立直角坐标系。在直角坐标系里,图上 任意一点的坐标代表了决策变量的一组值,例 1 的每个约束条件都代表一个半平 面。 (2)对每个不等式(约束条件),先取其等式在坐标系中作直线,然后确定不等式 所决定的半平面。 x2 x1 X1≥0 X1=0 x2 x1 X2≥0 X2=0
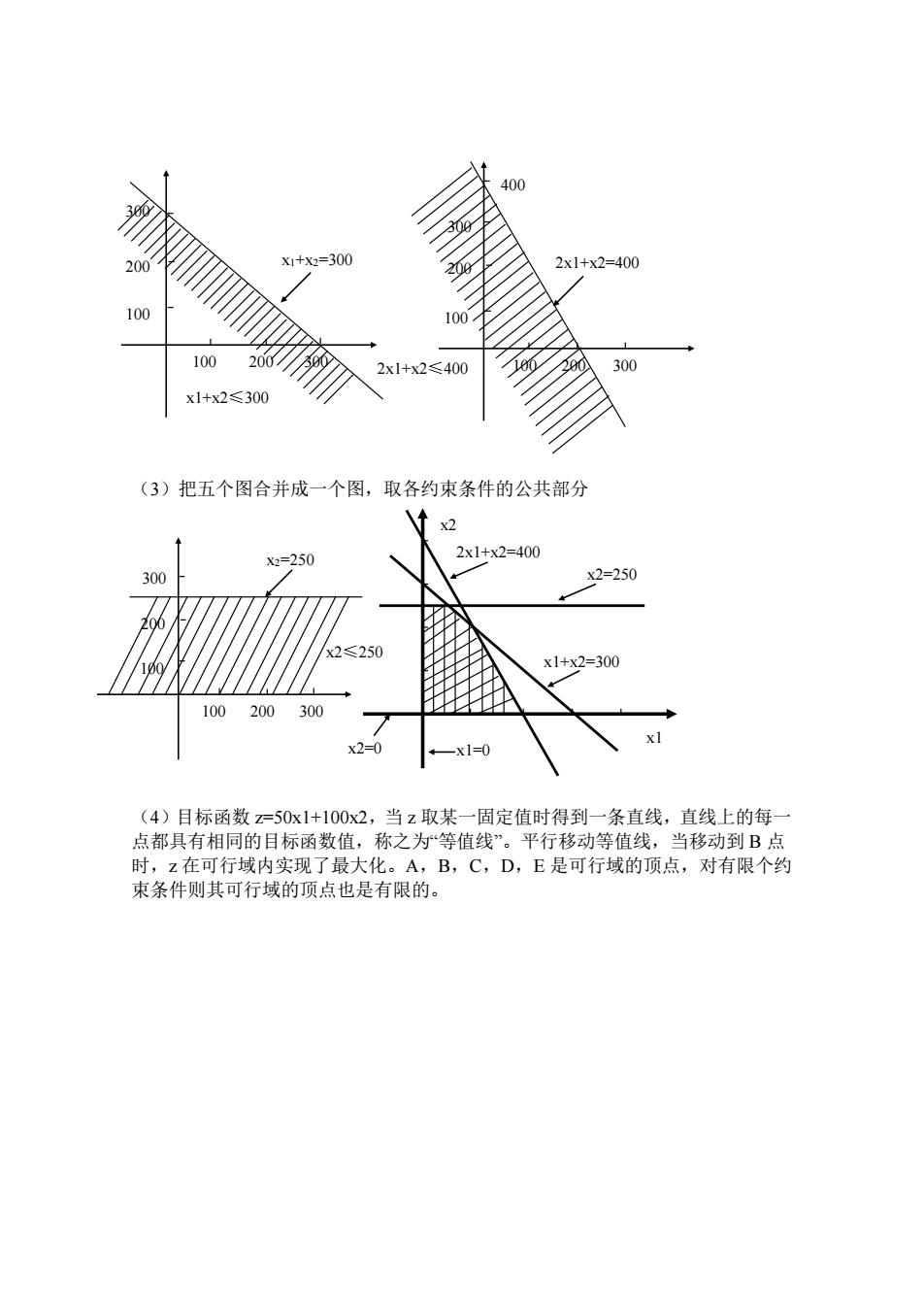
=300 2x1+x2=-400 100 100 200 2x1+x2≤400 300 x1+x2≤300 (3)把五个图合并成一个图,取各约束条件的公共部分 x=250 2x1+x2-400 300 x2=250 2≤250 x1+x2-300 100200300 x2-0 (4)目标函数x=50x1+100x2,当z取某一固定值时得到一条直线,直线上的每 点都具有相同的目标函数值,称之为“等值线”。平行移动等值线,当移动到B点 时,z在可行域内实现了最大化。A,B,C,D,E是可行域的顶点,对有限个约 束条件则其可行域的顶点也是有限的
(3)把五个图合并成一个图,取各约束条件的公共部分 (4)目标函数 z=50x1+100x2,当 z 取某一固定值时得到一条直线,直线上的每一 点都具有相同的目标函数值,称之为“等值线”。平行移动等值线,当移动到 B 点 时,z 在可行域内实现了最大化。A,B,C,D,E 是可行域的顶点,对有限个约 束条件则其可行域的顶点也是有限的。 100 2x1+x2≤400 100 200 2x1+x2=400 300 200 300 400 100 200 300 100 200 300 x1+x2≤300 x1+x2=300 100 100 x2≤250 x2=250 200 300 200 300 x1 x2 x2=0 x1=0 x2=250 x1+x2=300 2x1+x2=400
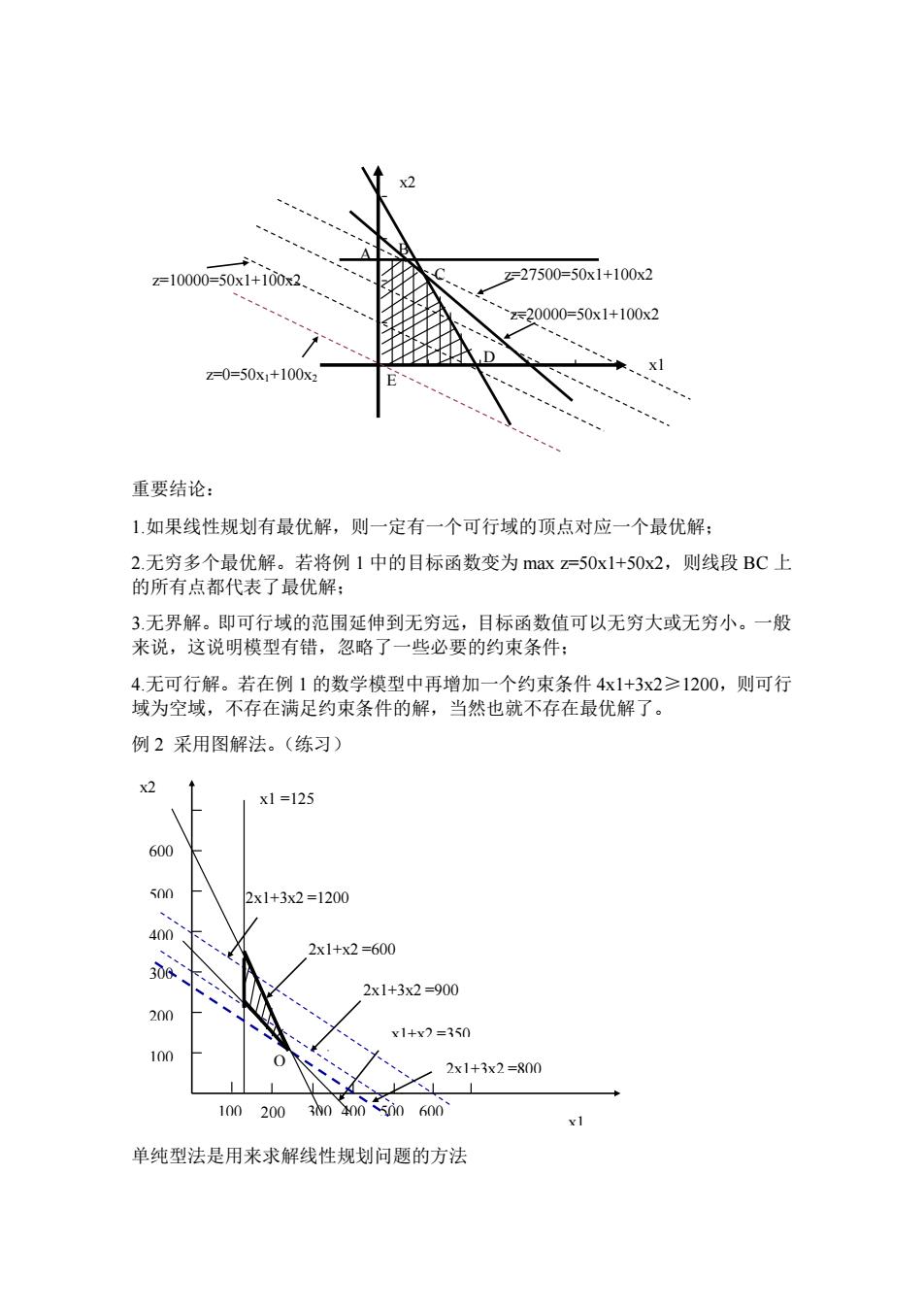
x2 Z=10000=50x1+100x2. F27500=50x1+100x2 z20000=50x1+100x2 A.D =0=50x1+100x 、 重要结论: 1如果线性规划有最优解,则一定有一个可行域的顶点对应一个最优解: 2.无穷多个最优解。若将例1中的目标函数变为maxz=50x1+50x2,则线段BC上 的所有点都代表了最优解: 3.无界解。即可行域的范围延伸到无穷远,目标函数值可以无穷大或无穷小。一般 来说,这说明模型有错,忽略了一些必要的约束条件: 4.无可行解。若在例1的数学模型中再增加一个约束条件4x1+3x2≥1200,则可行 域为空域,不存在满足约束条件的解,当然也就不存在最优解了。 例2采用图解法。(练习) x21 x1=125 600 2x1+3x2=1200 40m 2x1+x2=600 2x1+3x2=900 20 v1+x7=350 10m 2x1+3x2=800 100200302000600 单纯型法是用来求解线性规划问题的方法
重要结论: 1.如果线性规划有最优解,则一定有一个可行域的顶点对应一个最优解; 2.无穷多个最优解。若将例 1 中的目标函数变为 max z=50x1+50x2,则线段 BC 上 的所有点都代表了最优解; 3.无界解。即可行域的范围延伸到无穷远,目标函数值可以无穷大或无穷小。一般 来说,这说明模型有错,忽略了一些必要的约束条件; 4.无可行解。若在例 1 的数学模型中再增加一个约束条件 4x1+3x2≥1200,则可行 域为空域,不存在满足约束条件的解,当然也就不存在最优解了。 例 2 采用图解法。(练习) 单纯型法是用来求解线性规划问题的方法 x1 x2 z=20000=50x1+100x2 z=27500=50x1+100x2 z=0=50x1+100x2 z=10000=50x1+100x2 C A B D E 100 200 300 400 500 600 100 200 300 400 600 500 x1 =125 x1+x2 =350 2x1+3x2 =800 2x1+3x2 =900 2x1+x2 =600 2x1+3x2 =1200 x1 x2 Q

其求解思路」 (1)找到一个可行域上的顶点(初始基可行解)作为待考查的解。 (2)将该解和与其相邻的顶点(基可行解)相比较,若该解优于相邻解,则该解 为整个线性规划问题的最优解:否则将更优的相邻解代替当前考查的解。 (3)重复第(2)步,直至找到解的情况,计算结束。 §3“管理运筹学”软件的操作方法 “管理运筹学2.0版(Window版),是1.0版(DOS版)的升级版。它包括:线性 规划、运输问题、整数规划(0-1整数规划、纯整数规划和混合整数规划)、目标 规划、对策论、最短路径、最小生成树、最大流量、最小费用最大流、关键路径、 存储论、排队论、决策分析、预测问题和层次分析法,共15个子模块。 1.软件使用演示:(演示例1) 第一步:点击“开始”>“程序”>“管理运筹学 2.0”,弹出主窗口。 例1. 目标函数: Max z=50x1+100x2 约束条件: St xl+ x2≤300(A) 2x1+ 2≤ 400 (B) x2≤250(C) xl ≥0 0 x2 ≥0 (E)
其求解思路: (1)找到一个可行域上的顶点(初始基可行解)作为待考查的解。 (2)将该解和与其相邻的顶点(基可行解)相比较,若该解优于相邻解,则该解 为整个线性规划问题的最优解;否则将更优的相邻解代替当前考查的解。 (3)重复第(2)步,直至找到解的情况,计算结束。 §3 “管理运筹学”软件的操作方法 “管理运筹学”2.0 版(Window 版),是 1.0 版(DOS 版)的升级版。它包括:线性 规划、运输问题、整数规划(0-1 整数规划、纯整数规划和混合整数规划)、目标 规划、对策论、最短路径、最小生成树、最大流量、最小费用最大流、关键路径、 存储论、排队论、决策分析、预测问题和层次分析法,共 15 个子模块。 1.软件使用演示:(演示例 1) 第一步:点击“开始”->“程序”-> “管理运筹学 2.0”,弹出主窗口。 例 1. 目标函数: Max z = 50 x1 + 100 x2 约束条件: s.t. x1 + x2 ≤ 300 (A) 2 x1 + x2 ≤ 400 (B) x2 ≤ 250 (C) x1 ≥ 0 (D) x2 ≥ 0 (E)
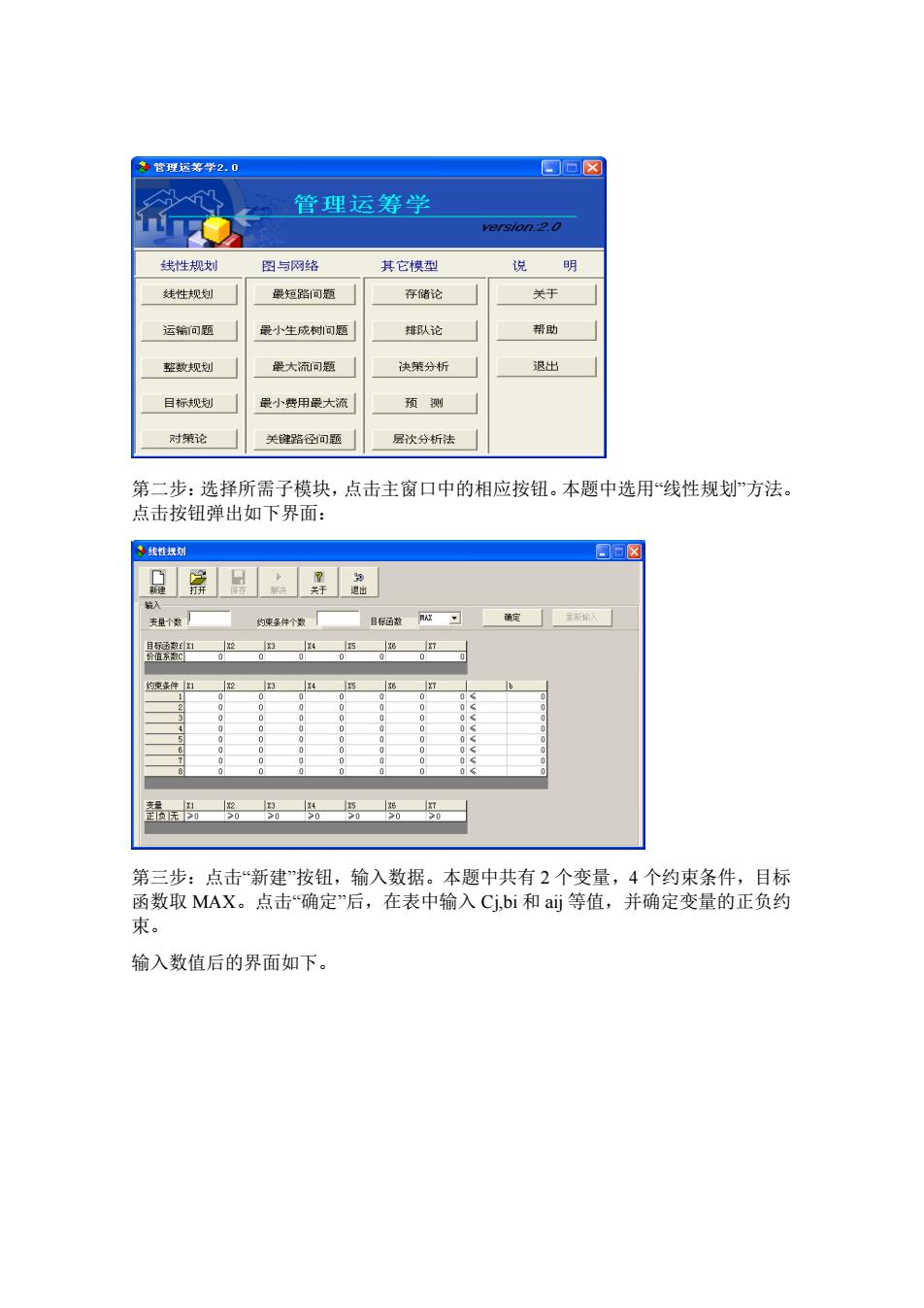
号营理运等学2可 回回冈 管理运筹学 线性规划 图与网络 其它模型 说明 线性规划 存储论 关于 运输题 最小生成树间题 队论 帮 空助规划 最大流回颗 决第分析桥 退出 目行规划 果小费用大流 预测 对第论 关路径题 层次分析法 第二步:选择所需子模块,点击主窗口中的相应按钮。本题中选用“线性规划方法。 点击按钮弹出如下界面: a 。原。 第三步:点击“新建按钮,输入数据。本题中共有2个变量,4个约束条件,目标 函数取MAX。点击“确定”后,在表中输入Cj,bi和a町等值,并确定变量的正负约 输入数值后的界面如下
第二步:选择所需子模块,点击主窗口中的相应按钮。本题中选用“线性规划”方法。 点击按钮弹出如下界面: 第三步:点击“新建”按钮,输入数据。本题中共有 2 个变量,4 个约束条件,目标 函数取 MAX。点击“确定”后,在表中输入 Cj,bi 和 aij 等值,并确定变量的正负约 束。 输入数值后的界面如下