
运筹学教案 张媛
运筹学教案 张媛

第一章绪论 §1运筹学释义与发展简史 一、书中释义 中国大百科全书:运筹学“用数学方法研究经济、民政和国防等部门在内外环境的约束条 件下合理分配人力、物力、财力等资源,使实际系统有效运行的技术科学,它可以用来预测 发展趋势,制定行动规划和优选可行方案。” 管理百科全书 “运筹学是应用分析、试验、量化的方法对经济管理系统中人力、物力、 财力等资源进行统筹安排,为决策者提供有依据的最优方案,以实现最有效的管理。 命名由来 Operational Research (Operations Research ( OR运用研究作业研究操作研究 运筹:运用筹划,策略取胜,反映这门学科的性质和内涵。 ”运学简史 1.名词正式使用 1938年,英国。空袭的早期预警,为解决来自不同雷达站的信息以及雷达站同整个防空 作战系统的协调配合问题,用“Operational Research"”一词作为这方面研究的描述。 2成立运第学小组 1940-英国,1942-美国、加拿大 3.第二次世界大战后,研究扩展到工业和政府部门。 (1)1945-50年代初,运筹学的创建期。 运筹学研究人数不多,范围小,出版物、学会宴塞无几。 (2)50年代初.50年代末,成长期。 电子计算机技术的迅速发展,运筹学中一些方法用于解决实际管理系统中的优化问题 促进运筹学的推广应用。 (3)60年代以来,运筹学开始普及和迅速发展的时期。 运筹学进一步的细分为各个分支,专业团体增多:期刊、书籍增多:运筹学课程纳入教 学计划之中。 4运筹学在中国的发展 1956年 -成立第一个运筹学小组 1958年 成立运筹学研究室 1962、1978一分别于北京、成都召开全国运筹学专业学术会议。 1980年4月—成立中国运筹学学会。 §2运筹学研究的基本特征与基本方法 一、基本特征 1.系统的整体观念 2.多学科的综合
第一章 绪论 §1 运筹学释义与发展简史 一、书中释义 中国大百科全书:运筹学“用数学方法研究经济、民政和国防等部门在内外环境的约束条 件下合理分配人力、物力、财力等资源,使实际系统有效运行的技术科学,它可以用来预测 发展趋势,制定行动规划和优选可行方案。” 管理百科全书:“运筹学是应用分析、试验、量化的方法对经济管理系统中人力、物力、 财力等资源进行统筹安排,为决策者提供有依据的最优方案,以实现最有效的管理。” 命名由来 Operational Research(英) Operations Research(美) O.R.运用研究 作业研究 操作研究 运筹:运用筹划,策略取胜,反映这门学科的性质和内涵。 二、运筹学简史 1.名词正式使用 1938 年,英国。空袭的早期预警,为解决来自不同雷达站的信息以及雷达站同整个防空 作战系统的协调配合问题,用“Operational Research”一词作为这方面研究的描述。 2.成立运筹学小组 1940-英国,1942-美国、加拿大 3.第二次世界大战后,研究扩展到工业和政府部门。 (1)1945-50 年代初,运筹学的创建期。 运筹学研究人数不多,范围小,出版物、学会寥寥无几。 (2)50 年代初-50 年代末,成长期。 电子计算机技术的迅速发展,运筹学中一些方法用于解决实际管理系统中的优化问题, 促进运筹学的推广应用。 (3)60 年代以来,运筹学开始普及和迅速发展的时期。 运筹学进一步的细分为各个分支,专业团体增多;期刊、书籍增多;运筹学课程纳入教 学计划之中。 4.运筹学在中国的发展 1956 年——成立第一个运筹学小组 1958 年——成立运筹学研究室 1962、1978——分别于北京、成都召开全国运筹学专业学术会议。 1980 年 4 月——成立中国运筹学学会。 §2 运筹学研究的基本特征与基本方法 一、基本特征 1.系统的整体观念 2.多学科的综合

3.模型方法 二、基本方法(步骤) 1分析和表述问题 2.建立模型 3求解模型和优化方案 4.测试模型及对模型进行必要的修正 5.建立对解的有效控制 6.方案的实施 §3运筹学的主要分支 线性规划(linear programming-LP) 非线性规划(nonlinear programming-NLP) 动态规划(dynamic programming) 图论与网络分析(graph theory and network analysis) 存储论(inventory theory) 排队论(queueing theory,or waiting line) 对策论(game theory) 决策论(decision theory)
3.模型方法 二、基本方法(步骤) 1.分析和表述问题 2.建立模型 3.求解模型和优化方案 4.测试模型及对模型进行必要的修正 5.建立对解的有效控制 6.方案的实施 §3 运筹学的主要分支 线性规划(linear programming-LP) 非线性规划(nonlinear programming-NLP) 动态规划(dynamic programming) 图论与网络分析(graph theory and network analysis) 存储论(inventory theory) 排队论(queueing theory, or waiting line) 对策论(game theory) 决策论(decision theory)
第二章线性规划与单纯形法 §1线性规划问题的提出及其数学模型 一、在管理中一些典型的线性规划应用 合理利用线材问题:如何在保证生产的条件下,下料最少 配料问题:在原料供应量的限制下如何获取最大利润 投资问题:从投资项目中选取方案,使投资回报最大 产品生产计划:合理利用人力、物力、财力等,使获利最大 劳动力安排:用最少的劳动力来满足工作的需要 运输问题:如何制定调运方案,使总运费最小 §2图解法及单纯型法解题思路 例1.某工厂在计划期内要安排I、Ⅱ两种产品的生产,已知生产单位产品所 需的设备台时及A、B两种原材料的消耗、资源的限制,如下表: 资源限制 设备 300台时 原料A 2 400千克 原料B 0 1 250千克 单位产品获利50元100元 问题:工厂应分别生产多少单位【、Ⅱ产品才能使工厂获利最多? 线性规划模型: 决策变量:x:I产品的产量,x2:Ⅱ产品的产量 目标函数:Maxz=50x1+100x2 约束条件:s.tx1+x2≤300 2x1+ x2≤400 x2≤250 x1,x2≥0 例2某公司由于生产需要,共需要A,B两种原料至少350 吨(A,B两种材料有一定替代性),其中A原料至少购进125
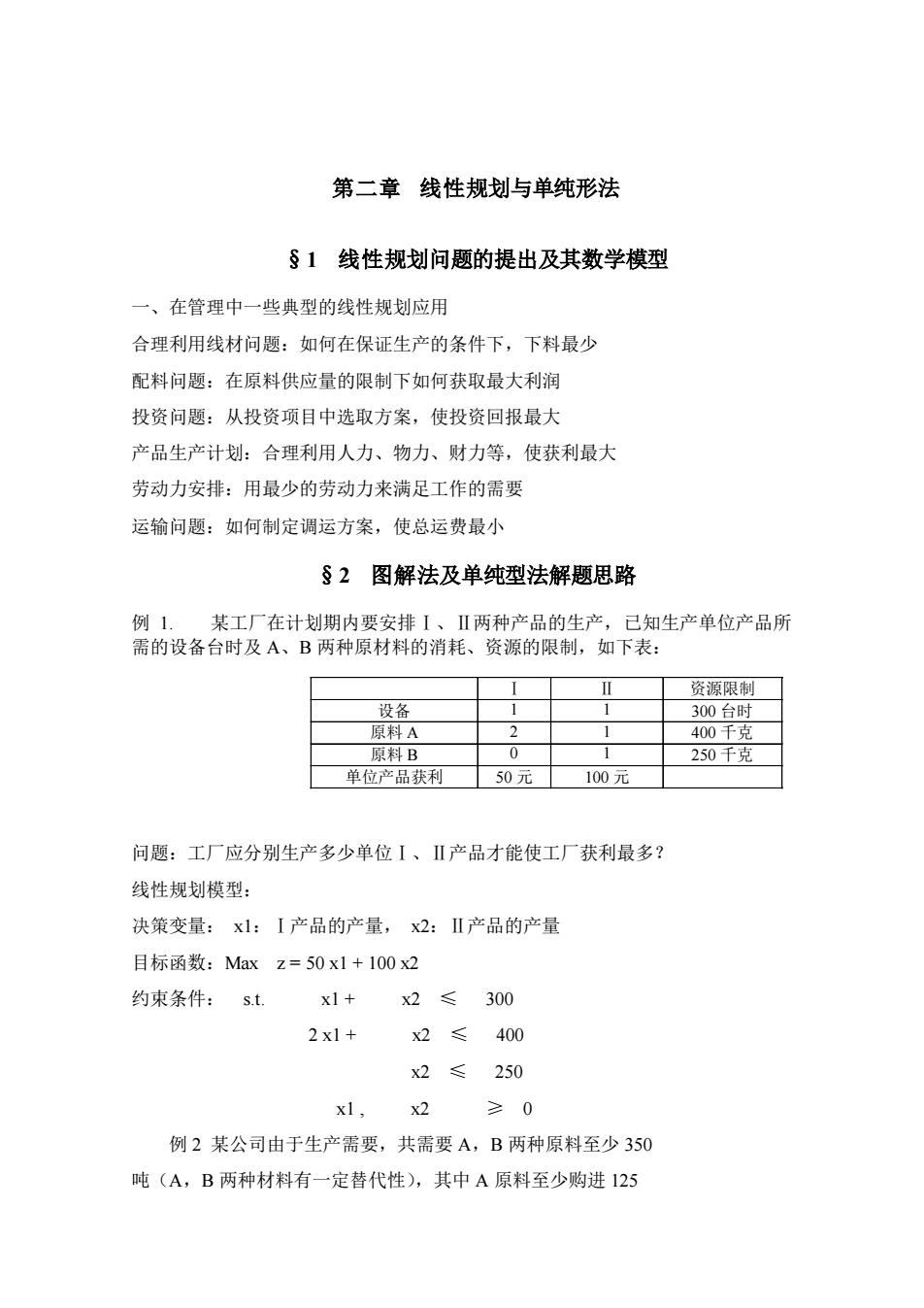
第二章 线性规划与单纯形法 §1 线性规划问题的提出及其数学模型 一、在管理中一些典型的线性规划应用 合理利用线材问题:如何在保证生产的条件下,下料最少 配料问题:在原料供应量的限制下如何获取最大利润 投资问题:从投资项目中选取方案,使投资回报最大 产品生产计划:合理利用人力、物力、财力等,使获利最大 劳动力安排:用最少的劳动力来满足工作的需要 运输问题:如何制定调运方案,使总运费最小 §2 图解法及单纯型法解题思路 例 1. 某工厂在计划期内要安排Ⅰ、Ⅱ两种产品的生产,已知生产单位产品所 需的设备台时及 A、B 两种原材料的消耗、资源的限制,如下表: Ⅰ Ⅱ 资源限制 设备 1 1 300 台时 原料 A 2 1 400 千克 原料 B 0 1 250 千克 单位产品获利 50 元 100 元 问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多? 线性规划模型: 决策变量: x1:Ⅰ产品的产量, x2:Ⅱ产品的产量 目标函数:Max z = 50 x1 + 100 x2 约束条件: s.t. x1 + x2 ≤ 300 2 x1 + x2 ≤ 400 x2 ≤ 250 x1 , x2 ≥ 0 例 2 某公司由于生产需要,共需要 A,B 两种原料至少 350 吨(A,B 两种材料有一定替代性),其中 A 原料至少购进 125

吨。但由于A,B两种原料的规格不同,各自所需的加工时间 也是不同的,加工每吨A原料需要2个小时,加工每吨B原料需 要1小时,而公司总共有600个加工小时。又知道每吨A原料的 价格为2万元,每吨B原料的价格为3万元,试问在满足生产需 要的前提下,在公司加工能力的范围内,如何购买A,B两种 原料,使得购进成本最低? 决策变量:x1:原料A的购买量,x2:原料B购买量 目标函数:Min f=2x1+3x2 约束条件:st x1+x2≥350 xl ≥125 2x1+x2≤600 x1,x2≥0 建模过程 1理解要解决的问题,了解解题的目标和条件: 2定义决策变量(x1,x2,.,xm),每一组值表示一个方案: 3.用决策变量的线性函数形式写出目标函数,确定最大化或最小化目标: 4.用一组决策变量的等式或不等式表示解决问题过程中必须遵循的约束条件 一般形式 决策变量设置:x1,x2,.,xm 目标函数:Max(Mim)z=clxl+c2x2+.+cmXm 约束条件:st.allxl+al2x2+.+alnxn≤(=,≥)bl a21x1+a22x2+.+a2nxm≤(=,≥)b2 aml xl+am2x2+.+amn xn≤(=,≥)bm xl,x2,.,xm≥0 对于只有两个决策变量的线性规划问题,可以在平面直角坐标系上作图表示 线性规划问题的有关概念,并求解。 下面通过例1详细讲解其方法: 例1.目标函数:
吨。但由于 A,B 两种原料的规格不同,各自所需的加工时间 也是不同的,加工每吨 A 原料需要 2 个小时,加工每吨 B 原料需 要 1 小时,而公司总共有 600 个加工小时。又知道每吨 A 原料的 价格为 2 万元,每吨 B 原料的价格为 3 万元,试问在满足生产需 要的前提下,在公司加工能力的范围内,如何购买 A,B 两种 原料,使得购进成本最低? 决策变量: x1:原料 A 的购买量,x2:原料 B 购买量 目标函数: Min f = 2x1 + 3 x2 约束条件: s.t. x1 + x2 ≥ 350 x1 ≥ 125 2 x1 + x2 ≤ 600 x1 , x2 ≥ 0 建模过程 1.理解要解决的问题,了解解题的目标和条件; 2.定义决策变量( x1 ,x2 ,. ,xn ),每一组值表示一个方案; 3.用决策变量的线性函数形式写出目标函数,确定最大化或最小化目标; 4.用一组决策变量的等式或不等式表示解决问题过程中必须遵循的约束条件 一般形式 决策变量设置: x1, x2, . , xn 目标函数: Max (Min) z = c1 x1 + c2 x2 + . + cn xn 约束条件: s.t. a11 x1 + a12 x2 + . + a1n xn ≤( =, ≥ )b1 a21 x1 + a22 x2 + . + a2n xn ≤( =, ≥ )b2 . . am1 x1 + am2 x2 + . + amn xn ≤( =, ≥ )bm x1 ,x2 ,. ,xn ≥ 0 对于只有两个决策变量的线性规划问题,可以在平面直角坐标系上作图表示 线性规划问题的有关概念,并求解。 下面通过例 1 详细讲解其方法: 例 1.目标函数: