
导航 课堂·重难突破 探究一利用定义法求二面角 S 【例1】如图,在正三棱锥S-ABC中,底面边长 为3,棱锥的一个侧面的面积是底面积的气,M是 BC的中点,求二面角S-BCA的大小 A 分析:根据几何图形的结构特点,先作出二面角 M 的平面角,再通过解三角形求出角的大小 B
导航 课堂·重难突破 探究一 利用定义法求二面角 【例1】如图,在正三棱锥S-ABC中,底面边长 为3,棱锥的一个侧面的面积是底面积的 ,M是 BC的中点,求二面角S-BC-A的大小. 分析:根据几何图形的结构特点,先作出二面角 的平面角,再通过解三角形求出角的大小. 𝟐 𝟑
导航 解:如图,SABC为正三棱锥, ',SB=SC,AB=AC,连接SMAM,又M为BC的中,点. '.SM⊥BC,AM⊥BC ‘.∠SMA为所求的二面角S-BC-A的平面角. 又棱锥的一个侧面的面积是底面积的号, 即3SM-24M,SM-2g D
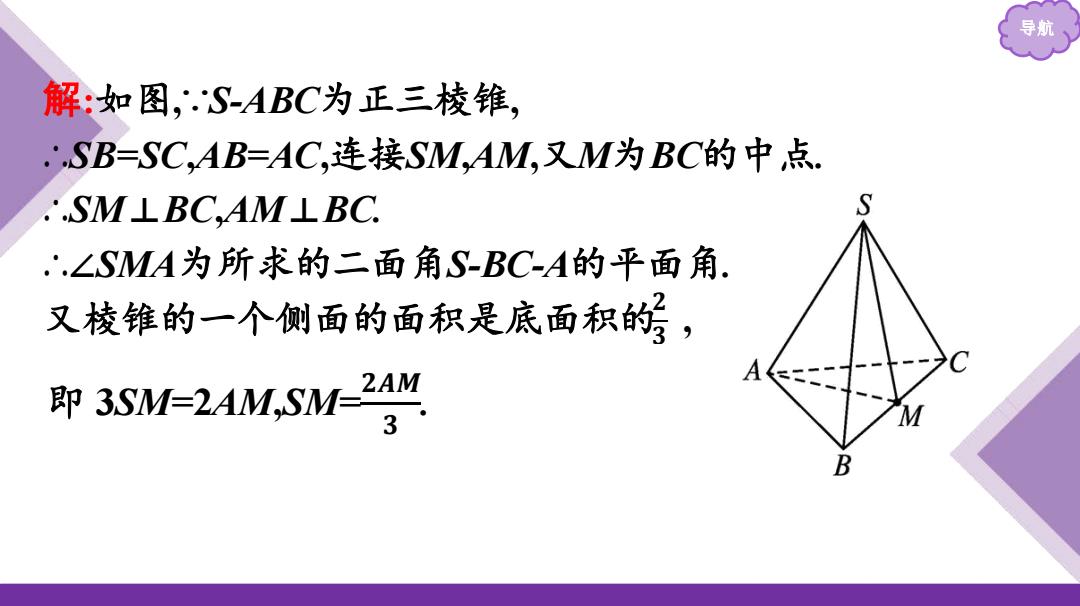
导航 解:如图,∵S-ABC为正三棱锥, ∴SB=SC,AB=AC,连接SM,AM,又M为BC的中点. ∴SM⊥BC,AM⊥BC. ∴∠SMA为所求的二面角S-BC-A的平面角. 又棱锥的一个侧面的面积是底面积的 , 𝟐 𝟑 即 3SM=2AM,SM=𝟐𝑨𝑴 𝟑

导航 又AM=ABsin60=_3 2) sM3,4=B=(份+W32= 2721 在△SAM中,c0S∠AMS-MS2+MA2-SA2 3+44 2MS·MA 2xw3×39 22 ·.∠AS学即二面角SBCA的大小为号
导航 又 AM=ABsin 60°= 𝟑 𝟑 𝟐 , ∴SM= 𝟑,SA=SB= 𝟑 𝟐 𝟐 + ( 𝟑) 𝟐 = 𝟐𝟏 𝟐 . 在△SAM 中,cos∠AMS=𝑴𝑺 𝟐 +𝑴𝑨 𝟐 -𝑺𝑨 𝟐 𝟐𝑴𝑺·𝑴𝑨 = 𝟑+ 𝟐𝟕 𝟒 - 𝟐𝟏 𝟒 𝟐× 𝟑× 𝟑 𝟑 𝟐 = 𝟏 𝟐 , ∴∠AMS=𝛑 𝟑 ,即二面角 S-BC-A 的大小为𝛑 𝟑

导航 反思感悟 当两个平面所在的图形是以棱为公共边的等腰三角形或全等 多边形时,利用定义求二面角的平面角更容易一些.利用定义 求二面角大小时,分三步,即一作(找),二证,三求
导航 当两个平面所在的图形是以棱为公共边的等腰三角形或全等 多边形时,利用定义求二面角的平面角更容易一些.利用定义 求二面角大小时,分三步,即一作(找),二证,三求

导航 【变式训练1】如图,在四面体P-ABC中,PC⊥平面 ABC,AB=BC=AC=PC,求二面角B-AP.C的大小. C B
导航 【变式训练1】如图,在四面体P-ABC中,PC⊥平面 ABC,AB=BC=AC=PC,求二面角B-AP-C的大小