
课程教案 课程名称:计量经济学 第六讲 本讲内容:_广义最小二乘法GLS)与异方差Heteroskedasticit 授课对象:金融专业 专业07年级本科生 授课时间:_200min 一、教学目的 通过本章介绍,使学生把握如果模型违反古典假定中残差项等方差的假定,给模型估 计带来的问题及其异方差的诊断与处理。 二、教学重点 异方差的出现对古典假设的违背。分组数据中的异方差。产生的原因和后果。异方差的诊断 与处理(Goldfield Guandt检验、Glejser检验)、GLS法 三、教学难点 GLS法的原理和应用 四、教学方法和手段 以电子课件为主,辅以必要的板书,EViews软件课堂演示 五、教学进程
课 程 教 案 第 页 课程名称: 计量经济学 第 六 讲 本讲内容: 广义最小二乘法(GLS)与异方差(Heteroskedasticity) 授课对象: 金融专业 专业 07 年级本科生 授课时间: 200 min 一、教学目的 通过本章介绍,使学生把握如果模型违反古典假定中残差项等方差的假定,给模型估 计带来的问题及其异方差的诊断与处理。 二、教学重点 异方差的出现对古典假设的违背。分组数据中的异方差。产生的原因和后果。异方差的诊断 与处理(Goldfield Guandt 检验、Glejser 检验)、GLS 法 三、教学难点 GLS 法的原理和应用 四、教学方法和手段 以电子课件为主,辅以必要的板书,EViews 软件课堂演示。 五、教学进程
课程教案 时间分 教学要求 教学内容 表达方式 配 (min) 芈握 1、广义最小二乘法(GLS)原理和应用举例 课件 Y=X B+u Var (u)=oQ=o PP (P为非奇异阵) 以Pl左乘原模型: PY-PIX B+Plu 即:Y◆=X*B+u 则:ar(u)=ar(Plu=E(Pluu'P") =021 把握 2、异方差 课件 (1)含义 即:在解释变量取不同值时方差不同,异方差是X的 函数。可通过散点图观察。 (2)异方差的来源 主要存在于横断面资料中 A、被解释变量的测量误差随时间而变化: 被省略 解释变量进入山中 D、分组数据中: E、人们的经济行为。 把握 3、 异方差的后果 课件 20 )参数估计量的方差变大: 2)t检验无法进行(σ2无法求得)方 3)降低预测精度。 学握操作 4、异方差的检验 课件+板书 1)图示检验法 :解释变量与e的散点图。 2)戈里瑟(Glejser)检验: a.Y OLS X1,X2,. .Xk,得序列e. b.建立方程寻找导致异方差的X: e=o e. 3)怀特(White)检验 a建立模型,例: e=ao+aX+aX:+aXi+a:Xi+a; b检验统计量: m=nR2 第
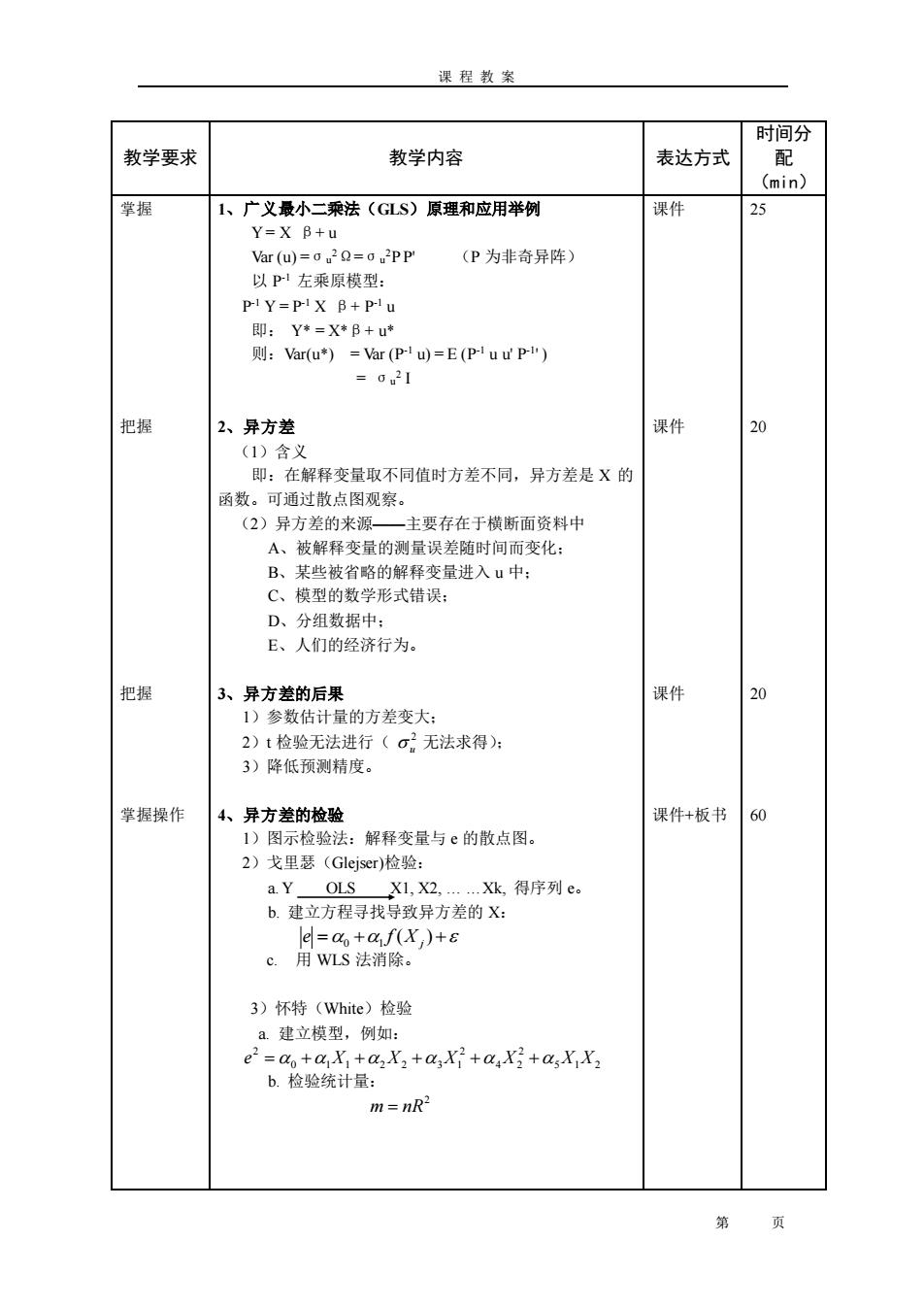
课 程 教 案 第 页 教学要求 教学内容 表达方式 时间分 配 (min) 掌握 把握 把握 掌握操作 1、广义最小二乘法(GLS)原理和应用举例 Y = X β+ u Var (u) =σu 2Ω=σu 2P P' (P 为非奇异阵) 以 P -1 左乘原模型: P -1 Y = P -1 X β+ P -1 u 即: Y* = X*β+ u* 则:Var(u*) = Var (P -1 u) = E (P -1 u u' P -1 ' ) = σu 2 I 2、异方差 (1)含义 即:在解释变量取不同值时方差不同,异方差是 X 的 函数。可通过散点图观察。 (2)异方差的来源——主要存在于横断面资料中 A、被解释变量的测量误差随时间而变化; B、某些被省略的解释变量进入 u 中; C、模型的数学形式错误; D、分组数据中; E、人们的经济行为。 3、异方差的后果 1)参数估计量的方差变大; 2)t 检验无法进行( 无法求得); 3)降低预测精度。 4、异方差的检验 1)图示检验法:解释变量与 e 的散点图。 2)戈里瑟(Glejser)检验: a. Y OLS X1, X2, . .Xk, 得序列 e。 b. 建立方程寻找导致异方差的 X: c. 用 WLS 法消除。 3)怀特(White)检验 a. 建立模型,例如: b. 检验统计量: 课件 课件 课件 课件+板书 25 20 20 60 5 1 2 2 4 2 2 0 1 1 2 2 3 1 2 e = + X + X + X + X + X X 2 m = nR2 u = + ( ) + 0 1 X j e f

课程教案 n为样本容量,R2为可决系数,m近似服从自由度为k(解 释变量的个数)的y分布。 c.判断:在Eviews的模型估计结果输出窗口中, View/Residual Test/White Heteroskedasticity 4)戈德菲尔特一夸特(Goldfield-quandt)检验(集团法) a.将X顺序排列,并保持与Y的对应关系: b.将数据分为两组(子样本),中间剔除c(n/3~n/4): c建立两个子方程,得s子 ∑e和∑ d.检验判断: := H:σ2≠o3 F>F拒绝。,有异方差: F<F 接受H。,无异方差。 5、模型估计一GLS 课件 25 (1)2已知(分组资料) [1 Var(u)=o =o22 n (2)2未知 6、EViews操作和案例分析 软件操作 50 第页
课 程 教 案 第 页 n 为样本容量,R2 为可决系数,m 近似服从自由度为 k (解 释变量的个数) 的 分布。 c. 判断:在 Eviews 的模型估计结果输出窗口中, 选 View/ Residual Test/ White Heteroskedasticity 4)戈德菲尔特—夸特(Goldfield-quandt)检验(集团法) a. 将 X 顺序排列,并保持与 Y 的对应关系; b. 将数据分为两组(子样本),中间剔除 c ( n/3~ n/4 ); c. 建立两个子方程,得 、 、 和 ; d. 检验判断: 5、模型估计—GLS (1) 已知(分组资料) (2) 未知 6、EViews 操作和案例分析 课件 软件操作 25 50 2 2 1 s 2 1 e 2 2 s 2 2 e 2 2 2 1 1 2 2 2 0 1 : : = H H ~ 2 2 2 1 = e e F 2) 2 2, 2 ( − − − n − c n c F 接受 ,无异方差。 拒绝 ,有异方差; H 0 0 F F F F H = = 1 1 1 ( ) 2 2 1 2 u m u n n n Var u